Classifying 3D shapes
Topic Notes
In this lesson, we will learn:
- That 3D shapes are shapes with 3 dimensions
- The properties/attributes of 3D shape (face, vertex, edge) and how to count them
- The different types of 3D shapes: prism shapes, pyramid shapes, and curved surface shapes
- All the subtypes of 3D shapes:
- triangular prism, rectangular prism, cube, pentagonal prism, hexagonal prism
- triangular pyramid, rectangular pyramid, square pyramid, pentagonal pyramid, hexagonal pyramid
- cylinder, cone, sphere
Notes:
- 3-dimensional shapes (3D shapes) are also called “solid figures” or “space figures”
- 1-dimensional (1D) is a straight line, 2-dimensional (2D) is a flat shape, and 3-dimensional (3D) is a solid figure like a cube in real life.
- Recall that dimensions are different planes or directions of measurement
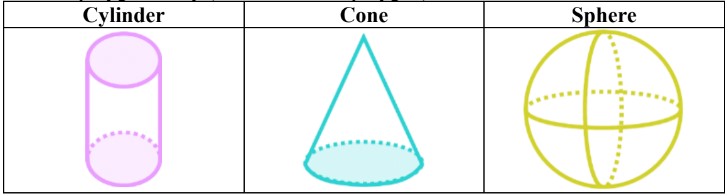
- There are three properties for 3D shapes: 1. Faces
- Faces are sides; the flat outer surfaces enclosed by lines
- Edges are lines where faces meet; touching sides
- Vertices are corners; two or more edges meet/converge at a vertex
2. Edges
3. Vertices (singular: vertex)
2. Pyramids
3. Curved surface shapes
- All other faces, besides the base, are rectangles
- All prisms have at least 2 pairs of parallel faces
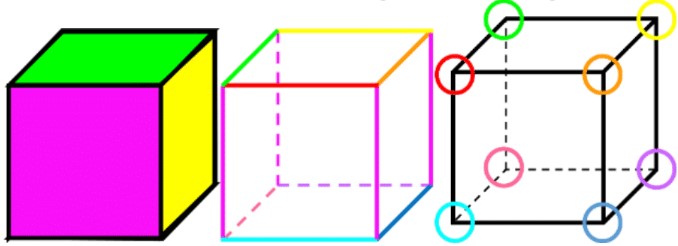
- A cube is a special prism (rectangular prism) where all edges are the exact same length (all faces are squares)
- Pyramids are 3D shapes with only one base
- All other faces, besides the base, are triangles
- All the triangle faces converge and connect at a top point (common vertex)

- Curved surface shapes are 3D shapes with curved surfaces
- These shapes usually have a circle shape as the base
- A cylinder is not a “circular prism” because prisms are made out of extending polygons only (a circle is not a polygon)
- There are special formulas which show the rules between the number of sides in the base shape and the number of faces (f) /vertices (Ve) /edges (E) for a 3D shape:

Introduction to Classifying 3D Shapes
Welcome to our lesson on classifying 3D shapes! This fascinating topic is essential for understanding the world around us. Our introduction video provides a comprehensive overview, setting the stage for an in-depth exploration of three-dimensional geometry. Throughout this lesson, we'll delve into the basics of 3D shapes, examining their unique properties and characteristics. You'll learn how to identify and differentiate between various 3D shapes, such as cubes, spheres, cylinders, and pyramids. We'll discuss key concepts like faces, edges, and vertices, which are crucial for classification. By understanding these fundamental elements, you'll develop the skills to accurately categorize 3D shapes based on their attributes. This knowledge is not only important in mathematics but also has practical applications in fields like architecture, engineering, and design. Get ready to embark on an exciting journey into the world of three-dimensional shapes and their classification!
Understanding 3D Shapes and Their Properties
Three-dimensional (3D) shapes are geometric figures that exist in three dimensions: length, width, and height. Unlike their two-dimensional (2D) counterparts, which are flat and only have length and width, 3D shapes occupy space and have volume. This fundamental difference allows 3D shapes to represent real-world objects more accurately, making them essential in various fields such as architecture, engineering, and computer graphics.
To fully understand 3D shapes, it's crucial to grasp their three main properties: faces, edges, and vertices. These properties define the structure and appearance of 3D shapes and are key to their classification and analysis.
1. Faces: Faces are the flat or curved surfaces that form the exterior of a 3D shape. They are essentially the "sides" of the shape that you can see and touch. For example, a cube has six square faces, each representing one side of the shape. Faces can vary in shape and size depending on the 3D figure. Some shapes, like spheres, have a single curved face that encompasses the entire surface.
2. Edges: Edges are the lines where two faces meet. They form the boundaries of each face and contribute to the overall structure of the shape. In a cube, you'll find 12 edges, each representing the intersection of two adjacent faces. Edges can be straight or curved, depending on the shape. For instance, a cylinder has two circular edges at its top and bottom, as well as straight edges along its sides.
3. Vertices: Vertices (singular: vertex) are the points where three or more edges meet. They are essentially the corners of a 3D shape. A cube has eight vertices, one at each corner where three edges intersect. Not all 3D shapes have vertices; for example, a sphere has no vertices because it has no corners or points where edges meet.
To illustrate these properties, let's examine a cube in detail. A cube is a perfect example of a 3D shape with clearly defined faces, edges, and vertices:
- Faces: A cube has six square faces, all of equal size. Each face is a flat surface that forms one side of the cube. You can visualize these as the top, bottom, front, back, left, and right sides of the cube.
- Edges: A cube has 12 edges in total. These are the straight lines where two faces meet. If you run your finger along the boundary between two faces of a cube, you're tracing an edge.
- Vertices: A cube has eight vertices, one at each corner. Each vertex is the point where three edges and three faces come together.
Understanding these properties is crucial for several reasons. First, it allows us to accurately describe and classify 3D shapes. For instance, we can differentiate a cube from a rectangular prism by noting that all of a cube's faces are square and equal in size. Second, these properties help us calculate important measurements such as surface area calculation and volume. The number of faces, edges, and vertices also play a role in mathematical relationships like Euler's formula, which states that for many 3D shapes, the number of vertices minus the number of edges plus the number of faces equals two.
Moreover, recognizing these properties enables us to understand how 3D shapes relate to each other and how they can be transformed. For example, by altering the length of certain edges, we can turn a cube into a rectangular prism. By rounding off vertices and edges, we can morph a cube into a sphere.
In the digital world, 3D shapes and their properties are fundamental to computer-aided design (CAD), 3D modeling, and animation. Software programs use the concepts of faces, edges, and vertices to create and manipulate virtual 3D objects. This has applications in fields ranging from product design and architecture to video game development and special effects in movies.
As we continue to explore the world of 3D shapes, it's important to remember that while a cube is a straightforward example, many 3D shapes are more complex. Polyhedra, for instance, can have numerous faces, edges, and vertices in various configurations. Curved shapes like spheres and cylinders present their own unique properties and challenges in terms of measurement and surface area calculation.
Types of 3D Shapes: Prisms
Prisms are one of the fundamental types of three-dimensional shapes that play a crucial role in geometry and everyday life. These versatile structures are formed by extending a polygon base, creating a solid object with uniform cross-sections throughout its length. Understanding prisms is essential for anyone interested in mathematics, architecture, or engineering.
At its core, a prism is created by taking a two-dimensional polygon and extruding it along a straight line perpendicular to its surface. This process results in a three-dimensional shape with two identical polygon faces (called bases) connected by rectangular faces. The shape of the base determines the specific type of prism, leading to a wide variety of prism forms.
One of the most common types is the rectangular prism, also known as a cuboid. This shape has six rectangular faces, including two identical rectangular bases. Rectangular prisms are ubiquitous in our daily lives, appearing in the form of boxes, buildings, and many household items. Their uniform shape makes them ideal for storage and construction purposes.
Another important variant is the triangular prism. As the name suggests, this prism has triangular bases connected by three rectangular faces. Triangular prisms are often used in architectural designs and optical instruments due to their unique properties in reflecting and refracting light. They also serve as excellent examples for studying geometric principles in education.
Moving beyond these basic forms, we encounter more complex prisms such as pentagonal and hexagonal prisms. A pentagonal prism features pentagon-shaped bases linked by five rectangular faces, while a hexagonal prism has hexagon bases connected by six rectangular sides. These shapes are less common in everyday objects but play significant roles in specialized fields like crystallography and advanced engineering designs.
One of the defining characteristics of all prisms is that, regardless of their base shape, all faces besides the bases are rectangles. This property ensures that prisms have a consistent cross-section along their length, which is crucial for many practical applications. It also simplifies calculations related to surface area calculation, making prisms particularly useful in mathematical problem-solving.
Another key feature of prisms is that they always have at least two pairs of parallel faces. In the case of a rectangular prism, all three pairs of opposite faces are parallel. For other prisms, the base faces are always parallel to each other, and depending on the symmetry of the base polygon, additional pairs of parallel faces may exist. This parallelism is fundamental to the structural integrity of prisms and influences their behavior in various physical contexts.
The study of prisms extends beyond basic geometry into more advanced mathematical concepts. For instance, the principles of volume calculation for prisms form the foundation for understanding more complex three-dimensional shapes. Additionally, the surface area calculation of prisms introduces students to the concept of net diagrams, where a three-dimensional shape is "unfolded" into a two-dimensional representation.
In practical applications, prisms are everywhere. From the simple pencil (often a hexagonal prism) to complex architectural structures, these shapes are integral to our built environment. In optics, prisms are used to split light into its component colors or to redirect light beams. The strength and stability of prism shapes make them ideal for construction, while their predictable geometry is valuable in manufacturing and packaging industries.
Understanding prisms also paves the way for exploring more advanced three-dimensional shapes. Concepts learned from studying prisms can be applied to cylinders, pyramids, and even more complex polyhedra. This foundational knowledge is crucial for anyone pursuing fields such as engineering, architecture, or advanced mathematics.
In conclusion, prisms represent a fundamental category of three-dimensional shapes, characterized by their polygon bases and rectangular faces. From the simple rectangular and triangular prisms to more complex pentagonal and hexagonal variants, these shapes offer a wealth of geometric properties to explore. Their prevalence in both natural and man-made environments underscores the importance of understanding prisms in our study of geometry and its real-world applications.
Types of 3D Shapes: Pyramids
Pyramids stand as the second major category of three-dimensional shapes, captivating our imagination with their unique structure and historical significance. These remarkable geometric forms are characterized by a single base and multiple triangular faces that converge at a common vertex, creating a distinctive pointed top. The concept of pyramids extends far beyond their most famous examples in ancient Egypt, encompassing a variety of types based on the shape of their base.
At the heart of every pyramid is its base, which serves as the foundation for the entire structure. The base can take various polygonal shapes, giving rise to different types of pyramids. The simplest form is the triangular pyramid, also known as a tetrahedron, which features a triangular base and three triangular faces meeting at the apex. This shape is fundamental in geometry and appears in various natural and man-made structures.
Perhaps the most recognizable type is the square pyramid, immortalized by the ancient Egyptians in their monumental constructions at Giza. These awe-inspiring structures, with their square bases and four triangular faces, have stood for millennia as testaments to human ingenuity and architectural prowess. The square pyramid's symmetry and stability make it a popular choice in both ancient and modern architecture.
Expanding on this concept, we encounter the rectangular pyramid, which, as the name suggests, has a rectangular base. This variation offers more flexibility in design and can be seen in various architectural elements, from roof structures to decorative features. The elongated base of a rectangular pyramid provides unique aesthetic and functional possibilities in construction and design.
For those seeking more complex geometries, the pentagonal pyramid presents an intriguing option. With a five-sided base and five triangular faces converging at the top, this shape adds a level of sophistication to geometric designs. Similarly, the hexagonal pyramid, featuring a six-sided base, offers even more facets and angles, creating visually striking forms that can be found in both natural crystals and modern architectural marvels.
Regardless of the base shape, all pyramids share the fundamental characteristic of triangular faces meeting at a common vertex. This apex is a defining feature, giving pyramids their iconic pointed silhouette. The angle and height of this point can vary, affecting the overall proportions and appearance of the pyramid. In some cases, such as in the step pyramids of ancient Egypt, the smooth triangular faces are replaced with a series of receding levels, creating a staircase-like profile while maintaining the essential pyramidal form.
The concept of pyramids extends far beyond mere geometric curiosity. These shapes have played significant roles throughout human history, from the colossal monuments of ancient civilizations to modern architectural wonders. The Great Pyramid of Giza, for instance, stands as an enduring symbol of ancient Egyptian culture and engineering prowess. Built as a tomb for Pharaoh Khufu around 2560 BCE, it remains one of the Seven Wonders of the Ancient World and continues to inspire awe and fascination.
In contemporary architecture, pyramidal forms continue to captivate designers and engineers. Modern interpretations of pyramids can be seen in structures like the Louvre Pyramid in Paris, a glass and metal pyramid that serves as the main entrance to the famous museum. This innovative use of the pyramidal shape demonstrates how ancient geometric principles can be adapted to create striking, functional designs in the modern world.
The study of pyramids also holds importance in mathematics and engineering. The relationships between the base, faces, and height of a pyramid provide rich material for geometric calculations and structural analysis. Understanding these properties is crucial for architects and engineers working on projects that incorporate pyramidal elements, ensuring both aesthetic appeal and structural integrity.
As we explore the world of three-dimensional shapes, pyramids stand out for their elegance, versatility, and historical significance. From the simple tetrahedron to complex multi-faced structures, pyramids continue to inspire and challenge our understanding of geometry and spatial relationships. Whether encountered in ancient monuments, modern architecture, or natural formations, pyramids remain a testament to the enduring power of geometric forms in shaping our world and our imagination.
Types of 3D Shapes: Curved Surface Shapes
In the world of three-dimensional geometry, curved surface shapes stand out as the third main category of 3D shapes, distinct from polyhedra and prisms. These fascinating shapes are characterized by having at least one curved surface and are not based on polygons like their counterparts. Curved surface shapes add a new dimension to our understanding of 3D geometry and are prevalent in both natural and man-made structures around us.
There are three primary types of curved surface shapes: cylinders, cones, and spheres. Each of these shapes has unique properties and formation processes that set them apart from other 3D shapes. Let's explore each of these curved surface shapes in detail to understand their characteristics and how they differ from other 3D shapes.
Cylinders are perhaps the most common curved surface shape we encounter in everyday life. A cylinder is formed by rotating a rectangle around one of its sides. This rotation creates a shape with two circular bases connected by a curved lateral surface. The defining feature of a cylinder is that its cross-section perpendicular to the axis of rotation is always a circle. Examples of cylinders in real life include cans, pipes, and some building columns.
It's important to note the difference between cylinders and prisms, as they can sometimes be confused. While both have two parallel bases, a cylinder's bases are circular, and its lateral surface is curved. In contrast, a prism has polygonal bases and flat lateral faces. This distinction is crucial in understanding the unique properties of curved surface shapes.
Cones are another type of curved surface shape, formed by rotating a right-angled triangle around one of its shorter sides. This rotation creates a shape with a circular base and a curved lateral surface that tapers to a point called the apex or vertex. The distance from the apex to any point on the circular base's circumference is constant, giving cones their distinctive shape. Real-world examples of cones include ice cream cones, party hats, and some roof structures.
Spheres represent the epitome of curved surface shapes. A sphere is formed by rotating a semicircle around its diameter. This results in a perfectly symmetrical shape where every point on its surface is equidistant from the center. Spheres are unique among curved surface shapes as they have no bases or lateral surfaces - their entire surface is uniformly curved. Balls used in various sports, planets, and soap bubbles are all examples of spheres in our world.
The study of curved surface shapes is crucial in many fields, including architecture, engineering, and physics. Their unique properties allow for efficient design in structures and objects that require smooth, continuous surfaces. For instance, the aerodynamic properties of spheres and cylinders are essential in the design of vehicles and aircraft.
In mathematics, curved surface shapes introduce concepts like surface area and volume calculations that differ significantly from those of polyhedra and prisms. The formulas for calculating these properties involve constants like pi (π) and often require more advanced mathematical techniques, making them an important topic in higher-level geometry and calculus.
Understanding curved surface shapes also helps in appreciating the natural world around us. Many organic forms in nature, from fruits and vegetables to geological formations, exhibit properties of curved surface shapes. This connection between mathematics and nature highlights the importance of these shapes in our understanding of the world.
In conclusion, curved surface shapes - cylinders, cones, and spheres - form a distinct and important category of 3D shapes. Their unique properties, formation processes, and real-world applications make them an essential topic in geometry. By understanding these shapes, we gain a deeper appreciation for the complexity and beauty of three-dimensional space, both in mathematics and in the world around us.
Classifying 3D Shapes: Practical Applications
The ability to classify 3D shapes in everyday objects is a fundamental skill with numerous practical applications in our daily lives. From architecture and engineering to everyday objects, understanding and recognizing three-dimensional forms plays a crucial role in problem-solving and spatial reasoning. This article explores the real-world significance of 3D shape classification and provides examples to help you sharpen your skills.
In architecture, the classification of 3D shapes is essential for designing functional and aesthetically pleasing structures. Architects use a variety of geometric forms to create buildings that are both visually striking and structurally sound. For instance, the pyramid shape of the Louvre Museum in Paris combines stability with a modern aesthetic. Similarly, the cylindrical form of skyscrapers like the Gherkin in London maximizes interior space while providing resistance to wind forces.
Engineering relies heavily on 3D shapes in everyday objects for designing and manufacturing products. From simple household items to complex machinery, engineers must consider the geometric properties of different shapes to optimize functionality and efficiency. For example, the spherical shape of a ball bearing allows for smooth rotation with minimal friction, while the rectangular prism shape of a smartphone provides a comfortable grip and maximizes screen size.
In our everyday lives, we encounter a wide array of 3D shapes that serve specific purposes. The conical shape of a funnel helps direct liquids into narrow openings, while the cylindrical form of a can provides efficient storage and stacking capabilities. Understanding these shapes and their properties helps us use objects more effectively and even improvise solutions to problems we encounter.
Spatial reasoning, which involves visualizing and manipulating objects in our minds, is greatly enhanced by the ability to classify 3D shapes. This skill is crucial in fields such as interior design, where professionals must envision how different furniture pieces and decorative elements will fit and interact within a space. It's also valuable in everyday tasks like packing a suitcase efficiently or organizing items in a storage unit.
Problem-solving often requires the application of 3D shape knowledge. For instance, when assembling furniture or solving puzzles, understanding how different shapes fit together can significantly speed up the process. In more advanced scenarios, such as designing packaging for fragile items or creating ergonomic tools, the ability to analyze and utilize various 3D shapes is invaluable.
To help you practice classifying 3D shapes, try these simple exercises:
- Look around your room and identify five different 3D shapes. Can you name them and describe their properties?
- Imagine cutting a cone in half vertically. What shape would the cross-section be?
- Think of three everyday objects that are combinations of multiple 3D shapes. How do these shapes contribute to the object's function?
In the field of computer vision and artificial intelligence, 3D shape classification is becoming increasingly important. AI systems that can accurately identify and categorize three-dimensional objects have applications in autonomous vehicles, robotics, and augmented reality. These technologies rely on sophisticated algorithms to process visual data and make decisions based on the shapes they encounter in the environment.
The medical field also benefits from 3D shape classification. Medical imaging techniques like CT scans and MRIs produce three-dimensional representations of internal body structures. Healthcare professionals use their understanding of 3D shapes to interpret these images, diagnose conditions, and plan treatments. For example, recognizing the shape of a tumor can help determine its nature and guide surgical approaches.
In the world of manufacturing and 3D printing, classifying shapes is essential for quality control and efficient production. 3D printers create objects by layering materials based on digital models, which are essentially complex combinations of basic 3D shapes. Understanding how these shapes interact and combine is crucial for designing printable objects and troubleshooting issues in the printing process.
As we continue to advance in fields like virtual and augmented reality, the importance of 3D shape classification grows. Developers creating immersive experiences must have a deep understanding of how three-dimensional objects behave and interact in virtual spaces. This knowledge allows them to create realistic and engaging environments that users can navigate and manipulate intuitively.
By honing your skills in classifying 3D shapes, you're not only improving your spatial reasoning abilities but also
Conclusion
In this article, we've explored the fascinating world of 3D shapes and their classification. We've covered essential concepts such as faces, edges, and vertices, which form the building blocks of geometric solids. The introduction video provided a crucial visual understanding of these concepts, making them more tangible and relatable. Remember, developing spatial awareness and the ability to identify 3D shapes is not just an academic exerciseit's a skill that enhances our perception of the world around us. We encourage you to practice identifying and classifying 3D shapes in your daily environment, from household objects to architectural structures. This hands-on approach will reinforce your understanding and make geometry more engaging. As you become more comfortable with these basics, consider exploring more advanced geometry topics to further expand your knowledge. The world of 3D shapes is vast and excitingcontinue your journey of discovery and let your curiosity guide you to new geometric insights!
FAQs
-
What are the three main properties of 3D shapes?
The three main properties of 3D shapes are faces, edges, and vertices. Faces are the flat or curved surfaces that form the exterior of a shape. Edges are the lines where two faces meet. Vertices are the points where three or more edges intersect.
-
How do prisms differ from pyramids?
Prisms have two identical polygon bases connected by rectangular faces, resulting in a uniform cross-section throughout their length. Pyramids, on the other hand, have a single base (usually a polygon) and triangular faces that converge at a common vertex or apex.
-
What are curved surface shapes, and how do they differ from other 3D shapes?
Curved surface shapes include cylinders, cones, and spheres. They differ from other 3D shapes like prisms and pyramids by having at least one curved surface instead of being composed entirely of flat faces. These shapes are not based on polygons and have unique properties in terms of surface area and volume calculations.
-
Why is classifying 3D shapes important in real-world applications?
Classifying 3D shapes is crucial in various fields such as architecture, engineering, and product design. It helps in creating efficient and functional structures, optimizing space usage, and solving complex problems. Understanding 3D shapes also enhances spatial reasoning skills, which are valuable in everyday tasks and professional settings.
-
How can I improve my ability to identify and classify 3D shapes?
To improve your skills in identifying and classifying 3D shapes, practice observing objects in your daily environment and try to describe their geometric properties. Engage in activities like solving 3D puzzles or creating 3D models. Additionally, studying the properties of basic 3D shapes and how they combine to form more complex objects can enhance your understanding and recognition abilities.
Prerequisite Topics
When delving into the fascinating world of classifying 3D shapes, it's crucial to have a solid foundation in certain prerequisite topics. One of the most important concepts to grasp is the surface area of prisms. This fundamental skill is essential for understanding the properties and characteristics of various three-dimensional shapes.
Understanding the surface area of prisms is vital because it provides a basis for analyzing and categorizing 3D shapes. When classifying 3D shapes, we often need to consider their surface properties, including the total area of all faces. The ability to calculate surface area allows us to compare different shapes and identify their unique features.
For instance, when distinguishing between prisms and pyramids, knowing how to determine the surface area of a prism helps us recognize the differences in their structure. Prisms have two identical bases and rectangular faces, while pyramids have a single base and triangular faces. By calculating the surface area, we can better understand these distinctions and classify shapes more accurately.
Moreover, the concept of surface area calculation extends beyond just prisms. It serves as a stepping stone to understanding the surface areas of other 3D shapes, such as cylinders, spheres, and cones. This knowledge is invaluable when classifying more complex shapes and identifying their properties.
In addition to classification, understanding surface area is crucial for real-world applications. In fields like architecture, engineering, and design, professionals frequently need to classify and work with 3D shapes. The ability to calculate surface area helps in determining material requirements, estimating costs, and ensuring proper construction or manufacturing processes.
As you progress in your study of 3D shapes, you'll find that the skills learned from understanding the surface area of prisms will continually come into play. Whether you're analyzing the properties of polyhedra, exploring the relationships between different shapes, or solving complex geometric problems, this foundational knowledge will prove invaluable.
In conclusion, mastering the prerequisite topic of surface area of prisms is essential for successfully classifying 3D shapes. It provides a solid foundation for understanding more advanced concepts, enables accurate comparisons between different shapes, and prepares you for practical applications in various fields. By investing time in grasping this fundamental concept, you'll be well-equipped to tackle the challenges and intricacies of 3D shape classification with confidence.

