Subtracting with regrouping
Topic Notes
In this lesson, we will learn:
- How to regroup base ten block models ("borrowing" or "exchanging")
- How to subtract using base ten block models
Notes:
- Like addition, we will also need to regroup our base ten blocks for subtraction
- When we don't have enough to subtract, we need to borrow from the next place value up to make more (splitting up the base ten block models)
- Sometimes, this is called "exchanging"
1 ten can be exchanged into 10 ones
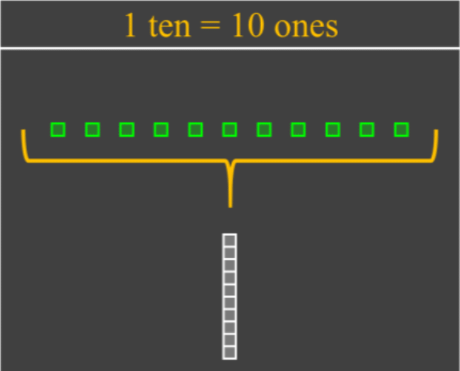
1 hundred can be exchanged into 10 tens
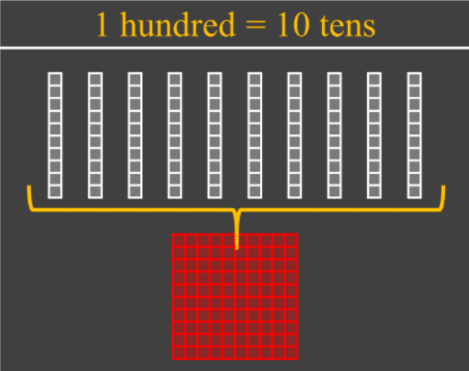
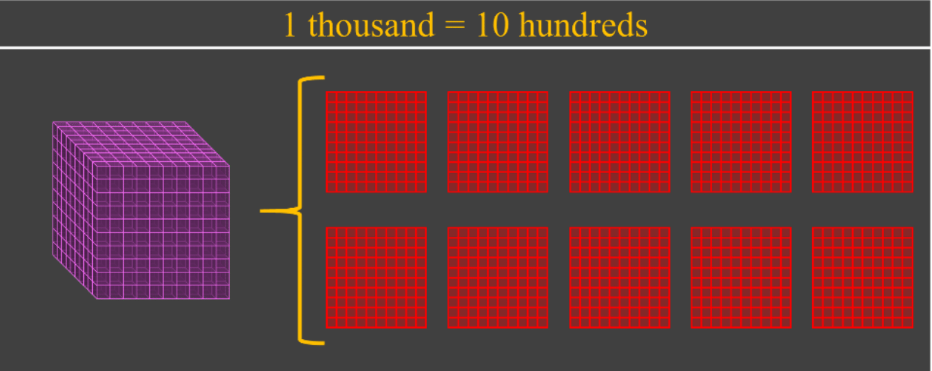
1 thousand can be exchanged into 10 hundreds
Introduction: Subtracting with Regrouping Using Base Ten Blocks
Welcome to our lesson on subtracting with regrouping using base ten blocks! This fundamental math skill is crucial for building a strong foundation in arithmetic. To kick things off, we'll start with an introduction video that clearly demonstrates the concept. This video is essential as it visually explains how regrouping works, making it easier to grasp. Base ten blocks are fantastic tools that help us understand place value and the process of regrouping. They allow us to physically represent numbers and see how we can "borrow from larger place values" when needed. As we work through examples together, you'll see how these blocks make subtracting with regrouping more tangible and less abstract. Remember, it's okay if it seems tricky at first with practice, you'll become more comfortable and confident in your ability to subtract with regrouping. Let's dive in and explore this exciting math concept together!
Understanding Base Ten Block Models
Base ten block models are powerful visual tools used to teach and understand the concept of place value understanding in our number system. These colorful, tangible manipulatives help students grasp the relationships between ones, tens, hundreds, and thousands, making abstract mathematical concepts more concrete and accessible.
Let's explore the different components of base ten blocks and how they represent various place values:
1. Unit Cubes (Ones): The smallest block in the set is a tiny cube, typically measuring 1 cm on each side. This cube represents a single unit or "one." It's often colored green or white. When students work with these unit cubes, they can physically count and group them, reinforcing the concept of individual units.
2. Rods (Tens): The next larger piece is a rectangular rod, usually 10 cm long and 1 cm wide and high. This rod represents "ten" and is equivalent to ten unit cubes lined up in a row. Rods are often colored blue. By comparing rods to unit cubes, students can visually understand that ten ones make one ten.
3. Flats (Hundreds): A flat is a square piece, measuring 10 cm by 10 cm and 1 cm thick. It represents "one hundred" and is equivalent to ten rods placed side by side or 100 unit cubes arranged in a 10x10 grid. Flats are typically red. This piece helps students visualize the concept of a hundred and its relationship to tens and ones.
4. Cubes (Thousands): The largest piece in the set is a large cube, measuring 10 cm on each side. This cube represents "one thousand" and is equivalent to ten flats stacked together, 100 rods, or 1,000 unit cubes. It's often colored yellow or orange. This piece brings the concept of a thousand to life, allowing students to see and feel its magnitude compared to smaller values.
Using these blocks, students can physically build numbers and see how place value understanding works. For example, to represent the number 1,234, a student would use:
- 1 large cube (1,000)
- 2 flats (200)
- 3 rods (30)
- 4 unit cubes (4)
This visual representation clearly shows how each digit in 1,234 relates to its place value. It becomes easy to understand why the '1' in 1,234 is worth much more than the '4'.
Base ten blocks are incredibly versatile. They can be used to teach addition, subtraction, multiplication, and division. For instance, when adding 23 and 45, students can physically combine 2 rods and 3 units with 4 rods and 5 units, then count the result: 6 rods and 8 units, or 68.
These models also help in understanding regrouping (or carrying and borrowing). When adding 17 and 15, students can see that combining 7 units and 5 units results in 12 units, which can be regrouped as 1 rod and 2 units. This concrete experience reinforces the abstract concept of regrouping in addition.
As students progress, they can use base ten blocks to explore larger numbers and more complex operations. The physical nature of these blocks allows for hands-on learning, making abstract mathematical concepts tangible and easier to grasp. This tactile approach is particularly beneficial for visual and kinesthetic learners.
In conclusion, base ten block models are invaluable tools in mathematics education. They provide a concrete representation of our number system's structure, helping students build a solid foundation in place value understanding. By manipulating these blocks, learners can develop a deep, intuitive grasp of numerical relationships, setting the stage for more advanced mathematical concepts in the future.
Representing Numbers with Base Ten Blocks
Representing numbers using base ten block models is an excellent way to visualize place values and understand the structure of our number system. Let's walk through this process using the example of 1,345 to demonstrate how to break down numbers and represent them with blocks.
First, let's understand what base ten blocks are. These manipulatives typically consist of four types of pieces:
- Unit cubes (ones): Small individual cubes representing 1
- Rods (tens): Bars made up of 10 unit cubes
- Flats (hundreds): Squares made up of 100 unit cubes (10 x 10)
- Large cubes (thousands): Cubes made up of 1000 unit cubes (10 x 10 x 10)
Now, let's break down 1,345 into its place values:
- 1 in the thousands place
- 3 in the hundreds place
- 4 in the tens place
- 5 in the ones place
To represent this number with base ten blocks, follow these steps:
- Start with the largest place value. For 1,345, place one large cube to represent 1,000.
- Move to the hundreds place. Add three flat squares to represent 300.
- For the tens place, add four rods to represent 40.
- Finally, for the ones place, add five individual unit cubes to represent 5.
When you're done, you'll have a visual representation of 1,345 using base ten blocks: one large cube, three flats, four rods, and five unit cubes. This model clearly shows how the number is composed and helps reinforce the concept of place value.
Using base ten blocks in this way can be particularly helpful for learners who benefit from hands-on, visual approaches. It makes abstract number concepts more concrete and can aid in understanding addition, subtraction, and even more complex operations like multiplication and division.
Remember, the key to successfully representing numbers with base ten blocks is to work systematically from the largest place value to the smallest, ensuring each digit is accurately represented by the appropriate block type. With practice, this method becomes an intuitive way to visualize place values and manipulate numbers, fostering a deeper understanding of our structure of number system.
Introduction to Regrouping in Subtraction
Regrouping in subtraction, also known as borrowing or exchanging, is a fundamental concept in mathematics that helps us solve problems when we need to subtract a larger digit from a smaller one. It's similar to regrouping in addition, but with a twist! Let's dive into this exciting world of number manipulation and see how it works.
Imagine you're solving the problem 12 minus 5. At first glance, it might seem simple, but there's a catch! We can't directly subtract a larger digit from a smaller one in the ones place. This is where regrouping comes to our rescue. We need to borrow from the tens place to make our subtraction possible.
Here's how regrouping works in this case:
- We start with 12, which is 1 ten and 2 ones.
- We need to subtract 5 ones, but we only have 2 ones. What do we do?
- We borrow 1 ten from the tens place. This 1 ten becomes 10 ones.
- Now, we add these 10 ones to the 2 ones we already had, giving us 12 ones.
- We can now easily subtract 5 from 12, leaving us with 7.
This process of taking a ten and converting it into ten ones is called "regrouping" or "exchanging." It's like breaking a dollar bill into 100 pennies you still have the same value, just in a different form!
The term "borrowing" is often used to describe this process, but it's not entirely accurate. We're not really borrowing in the traditional sense, because we don't give it back. That's why many math teachers prefer the terms "regrouping" or "exchanging."
Comparing regrouping in subtraction to addition, you'll notice some similarities. In addition, we sometimes need to regroup when the sum of two digits is 10 or more. For example, in 28 + 15, we regroup the 13 in the ones place as 1 ten and 3 ones. The principle is the same we're just moving values between place values.
Regrouping in subtraction might seem tricky at first, but with practice, it becomes second nature. Remember, it's all about understanding place value and being able to flexibly work with numbers. Don't be afraid to draw pictures or use manipulatives to help visualize the process. Math is all about understanding, not just memorizing steps!
As you continue your math journey, you'll find that regrouping is a skill that comes in handy in many situations, not just in simple subtraction. It's a building block for more complex mathematical operations and problem-solving strategies. So, embrace the concept, practice it, and watch how it opens up new possibilities in your math adventures!
Exchanging Between Place Values
Understanding place value is crucial in mathematics, and base ten blocks provide an excellent visual aid for grasping this concept. These blocks come in different sizes, representing various place values: small cubes for ones, long rods for tens, flat squares for hundreds, and large cubes for thousands. The beauty of this system lies in the ability to exchange between place values, reinforcing the relationship between different numerical positions.
Let's start with exchanging 1 hundred for 10 tens. Imagine a flat square representing one hundred. This single piece can be swapped for ten long rods, each representing ten. Visually, you're trading one larger piece for multiple smaller pieces, but the value remains the same. This exchange demonstrates that 100 is equivalent to 10 groups of 10, a fundamental concept in our base-ten number system.
Moving to a smaller scale, we can exchange 1 ten for 10 ones. Picture a long rod representing ten. This can be traded for ten small cubes, each representing one. This exchange visually reinforces that a single group of ten is equal to ten individual units. It's a powerful way to understand the relationship between tens and ones, showing how numbers are built up from smaller components.
For larger numbers, we can exchange 1 thousand for 10 hundreds. Imagine a large cube representing one thousand. This imposing block can be swapped for ten flat squares, each representing one hundred. This exchange beautifully illustrates how our number system scales up, with each place value being ten times the previous one. It helps students grasp the magnitude of larger numbers and how they relate to smaller ones.
These exchanges are not just abstract concepts; they have practical applications in mathematics. When performing addition or subtraction with regrouping, students can physically move these blocks to understand why we "carry" or "borrow" numbers. For instance, when adding 15 and 17, students can see why they need to exchange ten ones for one ten, creating a new group in the tens place.
The power of base ten blocks lies in their ability to make abstract numerical concepts tangible. Students can physically manipulate these blocks, seeing and feeling the relationships between different place values. This hands-on approach helps cement the understanding that our number system is based on groups of ten, with each place value being ten times the one to its right.
It's important to emphasize that while the physical form changes during these exchanges, the total value remains constant. Whether you have one hundred flat or ten rods, the quantity is the same. This principle reinforces the concept of conservation of number, a crucial understanding in mathematical development.
As students become more comfortable with these exchanges, they can start to visualize them mentally without the physical blocks. This skill is essential for mental math and understanding more complex mathematical operations. The foundation laid by working with base ten blocks supports future learning in areas like decimal places, percentages, and even algebra.
In conclusion, the process of exchanging between place values using base ten blocks is a powerful tool for building a strong foundation in mathematics. By physically manipulating these blocks and performing exchanges, students develop a deep, intuitive understanding place value of our number system. This hands-on approach bridges the gap between concrete and abstract thinking, setting the stage for more advanced mathematical concepts. Whether exchanging hundreds for tens, tens for ones, or thousands for hundreds, these activities reinforce the fundamental relationships that underpin our entire number system.
Practical Example of Regrouping in Subtraction
Let's walk through a detailed example of regrouping in subtraction using the numbers 254 and 66. We'll use base ten blocks to visualize each step, making it easier to understand the process of borrowing from the tens and hundreds places.
First, let's set up our problem:
254
- 66
-----
Now, let's represent 254 using base ten blocks:
2 hundreds blocks
5 tens rods
4 ones cubes
Step 1: Look at the ones place
We need to subtract 6 from 4, but 4 is smaller than 6. This means we need to regroup or "borrow" from the tens place.
Step 2: Borrow from the tens place
We'll take one ten rod (which represents 10) from the 5 tens we have. This leaves us with 4 tens rods in the tens place. We add this borrowed 10 to the 4 ones we already have, giving us 14 ones.
Our base ten blocks now look like this:
2 hundreds blocks
4 tens rods
14 ones cubes
Step 3: Subtract in the ones place
Now we can subtract 6 from 14:
14 - 6 = 8
We write 8 in the ones place of our answer.
Step 4: Move to the tens place
We need to subtract 6 tens from 4 tens. Again, we can't do this directly because 4 is smaller than 6.
Step 5: Borrow from the hundreds place
We'll take one hundred block (which represents 100) from the 2 hundreds we have. This leaves us with 1 hundred block in the hundreds place. We add this borrowed 100 to the 4 tens we have, giving us 14 tens.
Our base ten blocks now look like this:
1 hundreds block
14 tens rods
8 ones cubes
Step 6: Subtract in the tens place
Now we can subtract 6 tens from 14 tens:
14 - 6 = 8
We write 8 in the tens place of our answer.
Step 7: Subtract in the hundreds place
We have 1 hundred left, and we don't need to subtract any hundreds. So, we simply bring down the 1 to our answer.
Our final answer is 188.
Let's verify our solution:
254
- 66
-----
188
To double-check, we can add 188 and 66:
188 + 66 = 254
This confirms that our regrouping and subtraction are correct!
Remember, regrouping in subtraction is all about borrowing from the next place value when we need to. It's like asking your neighbor for a cup of sugar you're just borrowing from the next column over. With practice, this process will become second nature, and you'll be subtracting with confidence in no time!
Conclusion: Mastering Subtraction with Regrouping
Subtraction with regrouping using base ten blocks is a fundamental skill that builds a strong foundation for mathematical understanding. By visualizing the process with these blocks, students grasp the concept of place value understanding and the necessity of regrouping when subtracting larger numbers from smaller ones. The key lies in recognizing that we can't subtract a larger digit from a smaller one in a given place value understanding, necessitating the exchange of a unit from the next higher place value. This process reinforces the relationship between different place values and deepens overall number sense. As with any mathematical skill, practice is crucial. Encourage regular engagement with base ten blocks and various subtraction problems to solidify understanding. Remember, mastering this concept opens doors to more advanced mathematical operations. Stay patient, keep practicing, and celebrate each step of progress in your subtraction journey. With persistence and understanding, you'll soon find regrouping becomes second nature!
Example:
Introduction to Subtracting with Regrouping (using base ten block models): How to use base ten blocks to model numbers
Step 1: Understanding Place Values
To effectively use base ten blocks for modeling numbers, it's crucial to understand place values. Place values are the positions of digits in a number, which determine their value. The primary place values are ones, tens, hundreds, and thousands. Each place value uses a different type of base ten block model:
- Ones: Represented by small squares.
- Tens: Represented by sticks, which are made up of ten small squares.
- Hundreds: Represented by large squares, which are made up of ten sticks or 100 small squares.
- Thousands: Represented by large cubes, which are made up of ten large squares or 1,000 small squares.
Step 2: Representing Numbers with Base Ten Blocks
To represent a number using base ten blocks, break the number down into its place values. For example, to represent the number 1,345:
- Ones: The digit in the ones place is 5, so use five small squares.
- Tens: The digit in the tens place is 4, so use four sticks.
- Hundreds: The digit in the hundreds place is 3, so use three large squares.
- Thousands: The digit in the thousands place is 1, so use one large cube.
Step 3: Introduction to Regrouping
Regrouping, also known as borrowing or exchanging, is a method used in subtraction when the digit in the minuend (the number being subtracted from) is smaller than the digit in the subtrahend (the number being subtracted). For example, in the subtraction problem 12 - 5:
- Start with the ones place: 2 - 5. Since 2 is smaller than 5, you cannot subtract directly.
- Regroup by borrowing from the tens place. The number 12 can be thought of as 1 ten and 2 ones. Borrow 1 ten (which is 10 ones) and add it to the 2 ones, making it 12 ones.
- Now, subtract 5 from 12, which equals 7. The tens place now has 0 tens left.
Step 4: Regrouping with Base Ten Blocks
To visualize regrouping with base ten blocks:
- Represent the number 12 with base ten blocks: 1 stick (representing 10) and 2 small squares (representing 2).
- To subtract 5, you need more ones. Exchange 1 stick (10 ones) for 10 small squares.
- Now, you have 12 small squares. Subtract 5 small squares, leaving you with 7 small squares.
Step 5: Advanced Regrouping Concepts
Regrouping can also be applied to larger place values:
- Hundreds to Tens: If you need more tens, you can exchange 1 large square (100) for 10 sticks (10 tens).
- Thousands to Hundreds: If you need more hundreds, you can exchange 1 large cube (1,000) for 10 large squares (10 hundreds).
Step 6: Practical Application
Let's apply these concepts to a practical example:
- Consider the subtraction problem 1,345 - 678.
- Represent 1,345 with base ten blocks: 1 large cube (1,000), 3 large squares (300), 4 sticks (40), and 5 small squares (5).
- To subtract 678, start with the ones place: 5 - 8. Since 5 is smaller than 8, regroup by borrowing from the tens place. Exchange 1 stick (10 ones) for 10 small squares, making it 15 ones. Now, subtract 8 from 15, leaving 7 ones.
- Move to the tens place: 3 tens (30) - 7 tens (70). Since 30 is smaller than 70, regroup by borrowing from the hundreds place. Exchange 1 large square (100) for 10 sticks (100 tens), making it 130 tens. Now, subtract 70 from 130, leaving 60 tens.
- Finally, move to the hundreds place: 2 hundreds (200) - 6 hundreds (600). Since 200 is smaller than 600, regroup by borrowing from the thousands place. Exchange 1 large cube (1,000) for 10 large squares (1,000 hundreds), making it 1,200 hundreds. Now, subtract 600 from 1,200, leaving 600 hundreds.
FAQs
-
What are base ten blocks and how do they help in learning subtraction with regrouping?
Base ten blocks are physical manipulatives that represent different place values in our number system. They typically include unit cubes (ones), rods (tens), flats (hundreds), and large cubes (thousands). These blocks help in learning subtraction with regrouping by providing a visual and tactile representation of numbers, making it easier to understand the process of borrowing from higher place values when needed.
-
Why is regrouping necessary in subtraction?
Regrouping is necessary in subtraction when we need to subtract a larger digit from a smaller one in a particular place value. For example, when subtracting 28 from 52, we can't directly subtract 8 from 2 in the ones place. We need to regroup by borrowing 1 ten from the tens place, converting it to 10 ones, and adding it to the 2 ones we already have. This allows us to perform the subtraction correctly.
-
How do you explain regrouping to a child using base ten blocks?
To explain regrouping to a child using base ten blocks, start by representing the minuend (the number being subtracted from) with blocks. Then, when you need to subtract a larger digit from a smaller one, physically show how you can exchange a block from a higher place value for ten blocks of the lower place value. For example, exchange one ten-rod for ten unit cubes. This visual demonstration helps children understand that you're not creating new value, but just changing its form.
-
What are some common mistakes students make when learning subtraction with regrouping?
Common mistakes include forgetting to regroup when necessary, subtracting the smaller digit from the larger one regardless of which is on top, forgetting to reduce the value in the higher place after borrowing, or borrowing unnecessarily when there are enough units in a place value. Using base ten blocks can help students visualize these errors and correct them.
-
How can parents reinforce subtraction with regrouping at home?
Parents can reinforce subtraction with regrouping at home by using everyday objects as manipulatives (e.g., straws bundled in tens), practicing with real-life scenarios (like making change), using online interactive tools that simulate base ten blocks, and encouraging mental math strategies. Regular practice with varied problems and positive reinforcement can significantly improve a child's understanding and confidence with this concept.
Prerequisite Topics
Understanding the foundation of mathematics is crucial for mastering more complex concepts. When it comes to "Subtracting with regrouping (using base ten blocks)," one essential prerequisite topic stands out: place value. This fundamental concept plays a pivotal role in comprehending the process of regrouping and using base ten blocks effectively.
Place value is the cornerstone of our number system, determining the value of each digit based on its position within a number. When students grasp the concept of visualizing place values, they develop a deeper understanding of how numbers are structured and manipulated. This knowledge is invaluable when tackling more advanced mathematical operations, such as subtracting with regrouping.
In the context of subtracting with regrouping using base ten blocks, a solid grasp of place value becomes even more critical. Base ten blocks are physical representations of numbers, with different sized blocks representing ones, tens, hundreds, and so on. These manipulatives directly correlate to the place value system, making it easier for students to visualize and understand the regrouping process.
When students subtract numbers that require regrouping, they often need to "borrow" from a higher place value. This process is much easier to comprehend and execute when students have a strong foundation in place value. They can see how a ten can be broken down into ten ones, or how a hundred can be regrouped into ten tens. This visual and conceptual understanding makes the abstract process of regrouping more concrete and accessible.
Moreover, the ability to recognize and manipulate place values helps students avoid common errors in subtraction. For instance, understanding that the digit '2' in 25 represents two tens rather than just two units can prevent mistakes when regrouping is necessary. This awareness also aids in mental math strategies and estimation skills, which are valuable tools in everyday life.
By mastering place value, students build a strong mathematical foundation that extends far beyond subtraction with regrouping. This knowledge forms the basis for understanding decimals, fractions, and more advanced mathematical concepts. It also enhances overall number sense, allowing students to work more confidently and efficiently with numbers in various contexts.
In conclusion, a solid understanding of place value is indispensable for successfully learning and applying the concept of subtracting with regrouping using base ten blocks. By investing time in mastering this prerequisite topic, students set themselves up for success not only in this specific area but in their broader mathematical journey. The ability to visualize and manipulate place values will serve as a powerful tool throughout their academic and practical encounters with mathematics.

