Probability for compound events
Topic Notes
In this lesson, we will learn:
- Compound probability is for finding the chances of an event involving two simple probability scenarios
- How to draw a probability tree to show all possible outcomes for a compound event
- How to use an outcome table to show all possible outcomes for a compound event
- How to calculate compound probability fractions
Notes:
- Compound probability (or probability for compound events) is the chances of an event—involving two probability scenarios—happening.
- Some examples of compound situations: flipping 2 coins, rolling 2 dice, spinning the arrow on 2 spinners, or (combinations like) a coin flip and a die roll.
- Showing all possible outcomes for compound events will be different than probability for simple events. A probability tree or outcome table can be used
- A probability tree can be drawn vertically or horizontally. Each level represents each simple event: start at a point and draw branches for all possible outcomes. At the next level, the end of each previous branch will be a new starting point. Draw branches for all possible outcomes for the second simple event.
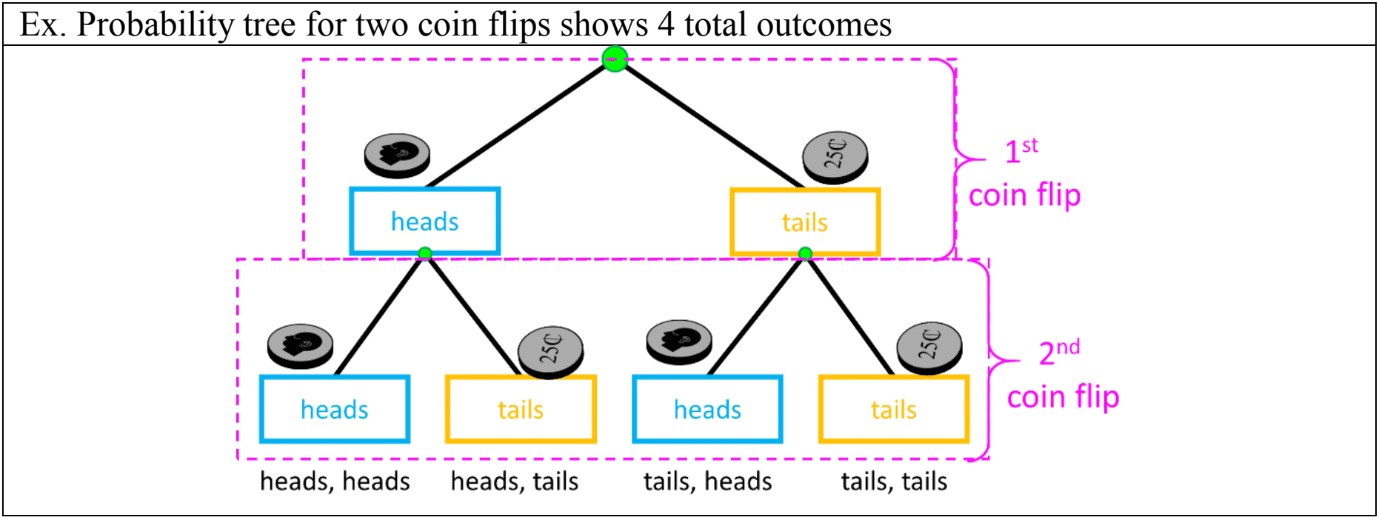
- Another way to find all outcomes for compound events is by using an outcome table, crossing all outcomes for the first event in the rows, by all the outcomes for the second outcomes in the columns.
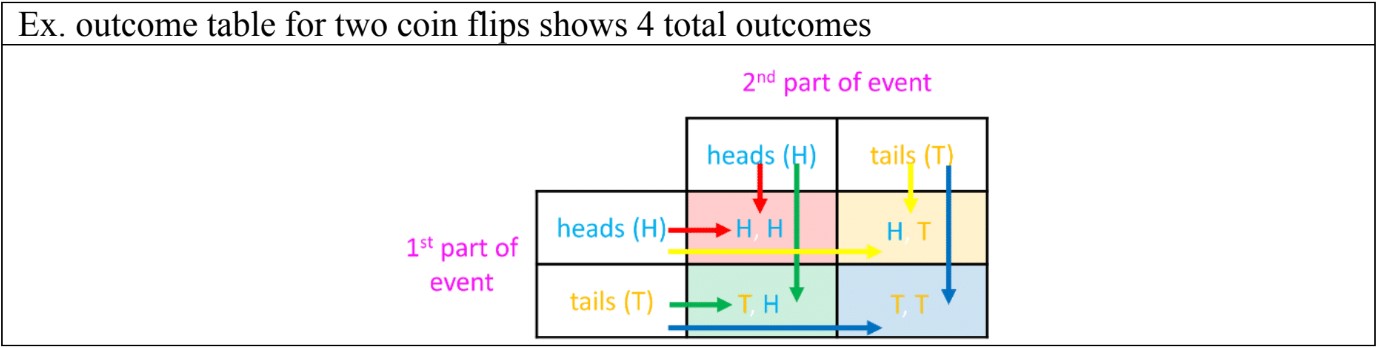
- The total number of outcomes can be calculated:
total outcomes = (#outcomes 1st event) × (#outcomes 2nd event) - The formula (event) = can also be used for compound probability
- Or, using fraction multiplication, compound probability for an event can also be found using the formula:
Compound Probability = (1st event) × (2nd event)
Introduction to Compound Probability
Welcome to our lesson on compound probability, a fundamental concept in statistics and probability theory. We'll begin with an engaging introduction video that sets the stage for understanding compound events and their significance in real-world scenarios. This video will provide you with a visual and intuitive grasp of the topic, making the subsequent lessons more accessible. Throughout this course, we'll delve into the basics of compound events, exploring how multiple outcomes or conditions can interact to create more complex probability scenarios. You'll learn how to identify compound events in various situations and, most importantly, how to calculate their probabilities accurately. By mastering compound probability, you'll gain a powerful tool for analyzing and predicting outcomes in fields ranging from finance to science. Whether you're a student, professional, or simply curious about probability, this lesson will equip you with essential knowledge to tackle more advanced concepts in the future.
Review of Simple Probability
Simple probability is a fundamental concept in mathematics that helps us understand the likelihood of events occurring. At its core, simple probability deals with situations where all possible outcomes are equally likely to happen. The probability fraction formula is a key tool in calculating these probabilities.
The probability fraction is expressed as: P(event) = (number of favorable outcomes) / (total number of possible outcomes). This formula provides a clear and concise way to represent the chances of a specific event occurring.
A classic example to illustrate simple probability is rolling a six-sided die. In this scenario, there are six possible outcomes (the numbers 1 through 6), and each outcome has an equal chance of occurring. Let's apply the probability fraction formula to some examples:
- The probability of rolling a 3: P(3) = 1/6, as there is only one favorable outcome (rolling a 3) out of six possible outcomes.
- The probability of rolling an even number: P(even) = 3/6 = 1/2, as there are three favorable outcomes (2, 4, and 6) out of six possible outcomes.
- The probability of rolling a number less than 5: P(less than 5) = 4/6 = 2/3, as there are four favorable outcomes (1, 2, 3, and 4) out of six possible outcomes.
The probability line is a visual representation of probabilities ranging from 0 to 1. On this line, 0 represents an impossible event, 1 represents a certain event, and all other probabilities fall between these two extremes. The probability line helps us understand and compare the likelihood of different events.
When describing the likelihood of events, we often use terms that correspond to different points on the probability line:
- Impossible: Probability of 0
- Very unlikely: Close to 0
- Unlikely: Less than 0.5
- Equally likely: Exactly 0.5
- Likely: Greater than 0.5
- Very likely: Close to 1
- Certain: Probability of 1
Understanding simple probability and using tools like the probability fraction formula and the probability line can help us make informed decisions in various fields, from statistics and data analysis to everyday situations involving chance and uncertainty. By applying these concepts, we can better predict outcomes, assess risks, and understand the likelihood of events occurring in our daily lives and professional endeavors.
Introduction to Compound Events
Compound events are a fundamental concept in probability theory, representing the occurrence of two or more simple events together. Unlike simple events, which involve a single outcome from a probability experiment, compound events combine multiple outcomes or actions. This distinction is crucial for understanding more complex probability scenarios and real-world applications.
To illustrate the concept of compound events, let's consider some common examples. One of the most straightforward instances is flipping two coins simultaneously. While flipping a single coin is a simple event with two possible outcomes (heads or tails), flipping two coins creates a compound event with four possible outcomes: both heads, both tails, or one of each in two different combinations.
Another classic example of compound events is rolling two dice. A single die roll is a simple event with six possible outcomes (1 through 6). However, when we roll two dice together, we create a compound event with 36 possible outcomes, ranging from (1,1) to (6,6). This increase in complexity demonstrates how compound events expand the range of possibilities compared to simple events.
Understanding compound events requires the ability to list all possible outcomes systematically. This process, known as creating a sample space, is essential for calculating probabilities accurately. For the coin flip example, we can list the outcomes as HH (both heads), HT (head then tail), TH (tail then head), and TT (both tails). Similarly, for rolling two dice, we would list all 36 combinations, from (1,1) to (6,6).
The importance of listing all possible outcomes becomes evident when we need to calculate specific probabilities within compound events. For instance, if we want to know the probability of getting a sum of 7 when rolling two dice, we need to identify all favorable outcomes (1+6, 2+5, 3+4, 4+3, 5+2, 6+1) out of the total 36 possibilities.
Compound events are not limited to just two simple events; they can involve multiple actions or outcomes. For example, drawing two cards from a deck without replacement or flipping a coin three times are more complex compound events. As the number of simple events combined increases, the total number of possible outcomes grows exponentially, making systematic listing and probability calculations more challenging.
In real-world scenarios, compound events are ubiquitous. Weather forecasts often deal with compound events, such as the probability of both rain and wind occurring on the same day. In sports, the outcome of a game might depend on multiple factors, creating a compound event. Understanding and analyzing these events is crucial in fields ranging from finance and insurance to scientific research and engineering.
As we delve deeper into probability theory, compound events serve as a bridge between basic concepts and more advanced topics. They introduce the idea of conditional probability, where the outcome of one event affects the probability of another. This concept is fundamental in many areas of statistics and data analysis.
By mastering the concept of compound events, including how to identify them, list their possible outcomes, and calculate their probabilities, we gain a powerful tool for understanding and predicting complex scenarios in both theoretical and practical applications. Whether you're analyzing game strategies, conducting scientific experiments, or making business decisions, a solid grasp of compound events will enhance your ability to interpret and utilize probability in meaningful ways.
Probability Trees for Compound Events
Probability trees are powerful visual tools used to represent and analyze compound events in probability theory. These tree diagrams help us organize information and calculate probabilities for complex scenarios involving multiple steps or outcomes. In this section, we'll explore how to create and use probability trees, using the classic example of flipping two coins to demonstrate the process.
To create a probability tree for compound events, follow these steps:
- Identify the sequence of events or decisions.
- Draw a root node representing the starting point.
- Create branches for each possible outcome of the first event.
- Label each branch with its probability.
- At the end of each branch, draw a new node.
- Repeat steps 3-5 for subsequent events.
- Calculate final probabilities by multiplying along each path.
Let's apply these steps to the example of flipping two coins:
1. We have two coin flips, each with two possible outcomes (heads or tails).
2. Start with a root node representing the beginning of the experiment.
3. For the first coin flip, draw two branches: one for heads (H) and one for tails (T).
4. Label each branch with a probability of 1/2, as a fair coin has an equal chance of landing on either side.
5. At the end of each branch, draw new nodes representing the outcome of the first flip.
6. For each of these nodes, repeat steps 3-5 for the second coin flip.
7. Calculate the final probabilities by multiplying the probabilities along each path.
The resulting probability tree for two coin flips would look like this:
1/2 H
1/2 H
1/2 T
O
1/2 H
1/2 T
1/2 T
To calculate probabilities using the tree diagram, we follow these guidelines:
- The probability of a specific path is the product of all probabilities along that path.
- The probability of multiple outcomes is the sum of their individual path probabilities.
For example, let's calculate some probabilities using our two-coin flip tree:
1. Probability of getting two heads (HH): 1/2 × 1/2 = 1/4
2. Probability of getting at least one tail: (1/2 × 1/2) + (1/2 × 1/2) + (1/2 × 1/2) = 3/4
3. Probability of getting exactly one head: (1/2 × 1/2) + (1/2 × 1/2) = 1/2
Probability trees are particularly useful for more complex scenarios. For instance, if we were to flip three coins, we could extend our tree to have eight final outcomes. This visual representation makes it easier to track all possible combinations and their respective probabilities.
When using probability trees for compound events, keep these tips in mind:
- Ensure that probabilities on branches stemming from the same node always sum to 1.
- Double-check that all possible outcomes are represented in the tree.
- Use the tree to identify independent events and dependent events.
- For larger trees, consider using software or spreadsheets to help with calculations.
Probability trees are versatile tools that can be applied to various real-world scenarios, such as:
- Analyzing game strategies
- Predicting weather patterns
- Evaluating independent events
Systematic Listing of Outcomes
When dealing with compound events in probability, it's crucial to have a systematic method for listing all possible outcomes without relying on a probability tree. One effective approach is the systematic listing method, also known as the array or table method. This technique is particularly useful for organizing and visualizing outcomes in a clear, structured manner. Let's explore this method using the example of two spinners to demonstrate its application and effectiveness.
Imagine we have two spinners, each divided into four equal sections labeled A, B, C, and D. Our goal is to list all possible outcomes when both spinners are spun together. The systematic listing method allows us to do this efficiently and comprehensively.
To begin, we create a table or array where one spinner's outcomes are listed along the top (as column headers) and the other spinner's outcomes are listed down the left side (as row labels). This setup forms a grid where each cell represents a unique combination of outcomes from both spinners.
Here's how we would set up our table for the two spinners:
- Column headers (Spinner 1): A, B, C, D
- Row labels (Spinner 2): A, B, C, D
Now, we systematically fill in each cell of the table with the corresponding outcome combination. For example:
- The cell where row A intersects with column A represents the outcome (A,A)
- The cell where row A intersects with column B represents the outcome (B,A)
- And so on for all 16 possible combinations
This method ensures that we don't miss any possible outcomes and provides a visual representation of all combinations. The completed table would look like this:
| A | B | C | D | |
|---|---|---|---|---|
| A | (A,A) | (B,A) | (C,A) | (D,A) |
| B | (A,B) | (B,B) | (C,B) | (D,B) |
| C | (A,C) | (B,C) | (C,C) | (D,C) |
| D | (A,D) | (B,D) | (C,D) | (D,D) |
The systematic listing method offers several advantages:
- Completeness: It ensures all possible outcomes are accounted for.
- Organization: Outcomes are presented in a structured, easy-to-read format.
- Visualization: The table provides a clear visual representation of all combinations.
- Counting: It's easy to count the total number of outcomes (in this case, 16).
- Pattern recognition: Patterns in outcomes can be more easily identified.
This method can be extended to more complex scenarios with additional events or more outcomes per event. For instance, if we added a third spinner, we could create a three-dimensional array or use multiple tables to represent all possible outcomes.
The systematic listing method is particularly useful in probability calculations. Once all outcomes are listed, it's straightforward to identify favorable outcomes for specific events and calculate probabilities. For example, if we wanted to find the probability of getting at least one A when spinning both spinners, we could quickly count the favorable outcomes from our table.
In conclusion, the systematic listing method, or array/table method, is a powerful tool for organizing and visualizing all possible outcomes of compound events. By using this approach with our two-spinner example, we've demonstrated how to create a comprehensive list of outcomes without the need for a probability tree. This method not only ensures
Calculating Compound Probabilities
Understanding how to calculate probabilities for compound events is crucial in various fields, from statistics to everyday decision-making. In this section, we'll explore two primary methods for calculating compound probabilities: the probability fraction formula and the multiplication method. We'll use examples from a two-spinner scenario to illustrate these concepts and emphasize the importance of understanding the total number of possible outcomes.
Let's start with the probability fraction formula. This method involves determining the number of favorable outcomes divided by the total number of possible outcomes. For compound events, we need to consider all possible combinations. In our two-spinner scenario, let's say we have one spinner with numbers 1-4 and another with colors red, blue, and green. The total number of possible outcomes is 4 x 3 = 12, as each number can be paired with each color.
For example, if we want to calculate the probability of getting an even number and the color blue, we first identify the favorable outcomes: (2, blue) and (4, blue). There are two favorable outcomes out of 12 total possibilities. Thus, the probability is 2/12 = 1/6.
The multiplication method, on the other hand, involves multiplying the individual probabilities of each event. This method is particularly useful when the events are independent events, meaning the outcome of one event doesn't affect the other. In our spinner example, the number on the first spinner doesn't influence the color on the second spinner, so they are independent events.
Using the same example of an even number and blue, we can calculate: P(even number) = 2/4 (as there are two even numbers out of four), and P(blue) = 1/3. Multiplying these probabilities gives us (2/4) x (1/3) = 1/6, which matches our result from the fraction method.
The multiplication method becomes especially powerful when dealing with more complex scenarios. For instance, if we wanted to calculate the probability of getting an odd number, blue, and then red in three spins, we could multiply P(odd) x P(blue) x P(red) = (2/4) x (1/3) x (1/3) = 1/18.
Understanding the total number of possible outcomes is crucial for accurate probability calculations. It forms the denominator in our fraction method and helps us verify our results when using the multiplication method. In more complex scenarios, such as drawing cards from a deck or rolling multiple dice, knowing how to calculate the total outcomes becomes even more critical.
For example, if we added a third spinner with shapes (circle, square, triangle), our total outcomes would increase to 4 x 3 x 3 = 36. This dramatically changes our probability calculations. The probability of getting a specific number, color, and shape combination would now be 1/36, illustrating how additional factors can significantly impact probabilities.
Compound probabilities find applications in various real-world scenarios. In weather forecasting, meteorologists might calculate the probability of rain and wind occurring together. In genetics, scientists use these methods to determine the likelihood of offspring inheriting specific combinations of traits. Even in sports analytics, compound probabilities help in predicting complex game outcomes.
As we delve deeper into probability theory, it's important to remember that these basic principles form the foundation for more advanced concepts. The ability to calculate compound probabilities accurately is essential for making informed decisions in fields ranging from finance to scientific research.
In conclusion, mastering the calculation of compound probabilities through both the fraction formula and multiplication method, along with a solid understanding of total possible outcomes, equips us with powerful tools for analyzing complex events and making data-driven decisions in various aspects of life and professional fields.
Conclusion and Application
In this lesson on compound probability, we've explored the fundamental concepts and techniques for calculating the likelihood of multiple events occurring together. The introduction video provided a crucial foundation, emphasizing the importance of understanding independent events. We've learned that a systematic approach is key to solving compound probability problems effectively. This involves clearly identifying the events, determining their relationship, and applying the appropriate multiplication rule or addition rule. Remember, practice is essential for mastering these concepts. Challenge yourself with various compound event scenarios, from dice rolls to card draws, to reinforce your understanding. By consistently applying these methods, you'll develop a strong intuition for probability calculations. As you progress, you'll find that compound probability is not just a mathematical concept, but a valuable tool for decision-making in real-world situations, from weather forecasting to risk assessment in business.
Understanding the difference between independent events and dependent events is crucial. The multiplication rule helps in calculating the probability of both types of events occurring together, while the addition rule is used for finding the probability of either event occurring. These rules are fundamental in the study of probability and are widely applicable in various fields. By mastering these rules, you can tackle more complex probability problems with confidence.
Introduction to Basic Probability for Compound Events: Simple vs. Compound Events in Probability
Understanding the basics of probability is essential for analyzing the likelihood of various events. In this guide, we will explore the differences between simple and compound events in probability, and how to calculate the probability for each type.
Step 1: Understanding Simple Probability
Simple probability refers to the likelihood of a single event occurring. It is calculated using the formula:
Probability (P) = Number of favorable outcomes / Total number of possible outcomes
For example, when rolling a six-sided die, there are six possible outcomes (1, 2, 3, 4, 5, 6). If we want to find the probability of rolling a 3, there is only one favorable outcome (rolling a 3) out of six possible outcomes. Therefore, the probability is 1/6.
In simple events, the sum of the probabilities of all possible outcomes equals 1 (or 100%). This is because one of the outcomes must occur.
Step 2: Introduction to Compound Probability
Compound probability involves the likelihood of two or more events occurring together. These events can happen simultaneously or sequentially. The key difference from simple probability is that we now consider multiple events and their combined outcomes.
For example, consider flipping two coins. Each coin flip is an independent event, meaning the outcome of one flip does not affect the other. The possible outcomes for two coin flips are: HH (heads-heads), HT (heads-tails), TH (tails-heads), and TT (tails-tails).
To calculate the probability of compound events, we use the formula:
Compound Probability (P) = Probability of Event 1 * Probability of Event 2
Step 3: Calculating Compound Probability
Let's apply the formula to an example. Suppose we want to find the probability of flipping two heads in two coin flips. The probability of flipping heads on one coin is 1/2. Since the events are independent, we multiply the probabilities:
P(Heads on Coin 1 and Heads on Coin 2) = (1/2) * (1/2) = 1/4
Therefore, the probability of flipping two heads is 1/4.
This method can be extended to more complex scenarios involving multiple events, such as rolling dice and flipping coins together.
Step 4: Listing All Possible Outcomes
When dealing with compound events, it is crucial to list all possible outcomes to ensure accurate calculations. For example, if we roll two six-sided dice, we need to consider all possible pairs of outcomes (e.g., (1,1), (1,2), ..., (6,6)).
By listing all possible outcomes, we can determine the total number of outcomes and identify the favorable ones. This helps in calculating the probability of specific compound events.
Step 5: Using Fraction Multiplication for Compound Probability
Another method to calculate compound probability is by using fraction multiplication. This method is particularly useful when dealing with multiple independent events. For example, if we want to find the probability of rolling a 3 on a die and flipping heads on a coin, we multiply the individual probabilities:
P(Rolling a 3 and Flipping Heads) = (1/6) * (1/2) = 1/12
This method simplifies the calculation process and ensures accurate results.
Step 6: Practical Examples and Applications
To solidify your understanding, let's consider a few practical examples:
Example 1: What is the probability of rolling two sixes with two dice?
Each die has a 1/6 chance of rolling a six. Therefore, the compound probability is:
P(Two Sixes) = (1/6) * (1/6) = 1/36
Example 2: What is the probability of flipping heads on a coin and rolling an even number on a die?
The probability of flipping heads is 1/2, and the probability of rolling an even number (2, 4, or 6) is 3/6 or 1/2. Therefore, the compound probability is:
P(Heads and Even Number) = (1/2) * (1/2) = 1/4
Conclusion
Understanding the difference between simple and compound probability is essential for analyzing various scenarios. Simple probability deals with single events, while compound probability involves multiple events. By using the appropriate formulas and methods, you can accurately calculate the likelihood of different outcomes. Practice with various examples to strengthen your understanding and application of these concepts.
FAQs
-
What is compound probability?
Compound probability is the likelihood of multiple events occurring together. It involves calculating the probability of two or more independent or dependent events happening simultaneously or in sequence. For example, the probability of rolling a 6 on a die and flipping heads on a coin is a compound probability.
-
How do you calculate compound probability for independent events?
For independent events, you multiply the individual probabilities of each event. For instance, if the probability of event A is 1/2 and event B is 1/3, the compound probability of both occurring is 1/2 × 1/3 = 1/6. This is known as the multiplication rule for independent events.
-
What's the difference between independent and dependent events in probability?
Independent events are those where the occurrence of one event does not affect the probability of the other event. For example, flipping a coin and rolling a die are independent. Dependent events, however, are those where the outcome of one event affects the probability of the other. Drawing cards from a deck without replacement is an example of dependent events.
-
How can probability trees help in solving compound probability problems?
Probability trees are visual tools that help organize and calculate probabilities for compound events. They show all possible outcomes and their respective probabilities, making it easier to compute final probabilities by multiplying along branches. They are particularly useful for complex scenarios with multiple steps or outcomes.
-
What are some real-world applications of compound probability?
Compound probability has numerous applications in various fields. In weather forecasting, it's used to predict the likelihood of multiple weather conditions occurring together. In genetics, it helps calculate the probability of inheriting specific combinations of traits. In finance, it's applied in risk assessment and investment strategies. Sports analysts use it to predict game outcomes based on multiple factors.
Prerequisite Topics for Understanding Probability of Compound Events
When delving into the fascinating world of probability for compound events, it's crucial to have a solid foundation in key prerequisite topics. These fundamental concepts serve as building blocks, enabling students to grasp more complex ideas with ease and confidence.
One essential prerequisite is understanding the probability of independent events. This concept forms the backbone of compound event probability, as it teaches students how to calculate the likelihood of multiple events occurring together when they don't influence each other. By mastering independent events, learners can more easily comprehend how probabilities combine in compound scenarios.
Another vital prerequisite is determining probabilities using tree diagrams and tables. This skill is invaluable when tackling compound events, as it provides a visual and systematic approach to breaking down complex probability scenarios. Tree diagrams, in particular, help students visualize the various outcomes and their associated probabilities, making it easier to calculate compound probabilities.
The connection between these prerequisites and compound event probability is profound. When students have a firm grasp on independent events, they can more easily identify when events in a compound scenario are independent or dependent. This knowledge is crucial for applying the correct probability rules and formulas.
Similarly, proficiency in using probability tree diagrams becomes a powerful tool when dealing with compound events. These diagrams allow students to map out all possible outcomes of a series of events, making it simpler to calculate the probability of specific combinations or sequences occurring.
By mastering these prerequisites, students develop a strong analytical framework for approaching compound event problems. They learn to break down complex scenarios into manageable parts, identify key relationships between events, and apply appropriate probability rules. This foundation not only aids in solving compound probability problems but also enhances overall critical thinking and problem-solving skills in statistics.
Moreover, a solid understanding of these prerequisites fosters confidence in tackling more advanced probability concepts. Students who are comfortable with independent events and probability diagrams find it easier to grasp concepts like conditional probability, which is often involved in compound event scenarios.
In conclusion, the journey to mastering probability for compound events is greatly facilitated by a strong foundation in these prerequisite topics. By investing time in understanding independent events and mastering the use of probability diagrams, students set themselves up for success in more advanced probability concepts. This comprehensive approach ensures a deeper, more intuitive understanding of compound events and their applications in various fields of study and real-world scenarios.

