- The units of measurements commonly used in chemistry.
- How to use the unit conversion method and the reason it is valuable.
- Practical examples of using the unit conversion method to do calculations in chemistry.
Notes:
- In any problem where information you have has different units to the information you're being asked for, you'll need to do a unit conversion.
- Chemistry calculations involve units like number of moles (units: mol), the mass of a substance (units: g), the volume of a gas, liquid or solution (units: L) and others.
- Calculations in chemistry can be solved by breaking down questions into segments:
- An unknown quantity to be found - the answer to the question.
- An initial quantity to be converted into the units of the unknown quantity.
- A conversion factor(s) linking the unknown quantity and the initial quantity.
- A conversion factor is an expression as a fraction that equates one unit to another. For example: and
- Because the value of both terms in the unit conversion are equal (60 seconds is equal to 1 minute), when multiplying by a unit conversion the value of the expression doesn't change.
- This also means you can arrange either term (seconds or mins) on the top or the bottom; arrange it so that your original units cancel and you convert to the new units. This is why it is known as a conversion factor.
- CONVERSION FACTORS WILL CHANGE THE UNITS WITHOUT CHANGING THE VALUE!
- To solve calculations using the unit conversion method, the following steps should be done in order:
- Identify the unknown quantity to be found – this should be written with units and put one side of an equation.
- Identify the initial quantity the question has given you – this starts, with units, on the other side of the equation.
- Apply the unit conversion(s) by multiplying it with the initial quantity you were given.
- This works even if multiple unit conversions are necessary – this method also encourages you to display your working clearly so any mistakes are usually easy to spot!
- For example: If there are 6 eggs in a box, how many eggs would be in 4.5 boxes?
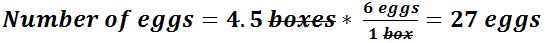
- For example (part 2): If an egg costs $2 each, how much does 3 dozen eggs cost?
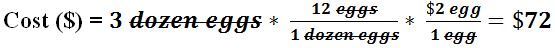
- This method can be used beyond chemistry to solve any problem involving a known quantity that can be converted into another unknown quantity.






