Adding decimals
Topic Notes
In this lesson, we will learn:
- How to add decimal numbers using base ten (block) models
- That adding decimal numbers is the same as adding whole numbers, which involves lining up the right place values and regrouping
Notes:
- To add decimals with base ten (block) models:
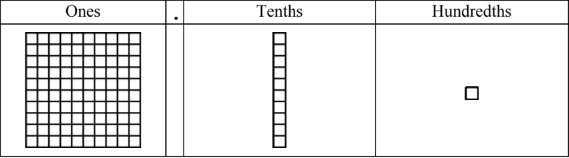
- Remember the three types of blocks used to represent the ones, tenths, and hundredths place values
- "One whole" or hundred block = ones place value
- Column (stick or rod) = tenths place value
- Single square = hundredths place value
- An addition statement is made of: addend + addend = sum
- Count all of the blocks that you are adding up, altogether
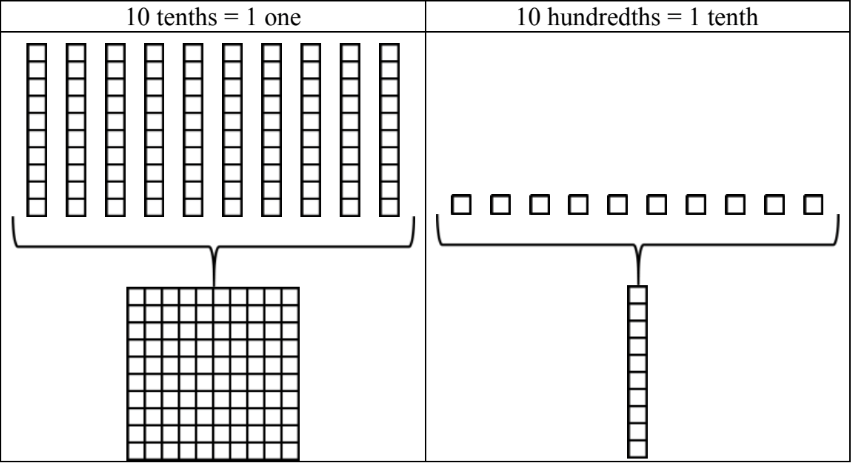
- Regroup to get to your final answer. 10 of any type of block will regroup into the next bigger type of block.
- To add decimals, line up the decimal point to make sure you are adding the right place values in the same columns. Regroup (carry over) numbers whenever necessary.
- Sometimes, you will have to write one or more zeroes to a number after the decimal point (trailing zeroes) when the addends don't have the same number of place values.
Introduction to Adding Decimals
Welcome to our lesson on adding decimals, a fundamental skill in mathematics. We'll begin with an essential introduction video that lays the groundwork for understanding this concept. This video is crucial as it visually demonstrates the process, making it easier to grasp. Our lesson will focus on adding decimals using base ten block models, a method that provides a concrete representation of abstract decimal numbers. You'll discover that adding decimals is remarkably similar to adding whole numbers, which will help build your confidence. By using base ten block models, we'll break down the process into manageable steps, allowing you to visualize how decimal place values align. This approach not only enhances understanding but also prepares you for more advanced decimal operations. As we progress, you'll see how this foundational knowledge applies to real-world scenarios, making mathematics more relevant and engaging.
Understanding Base Ten Block Models for Decimals
Base ten block models are fantastic tools that help us understand and visualize decimals in a fun and hands-on way. These models use special blocks to represent different parts of a number, making it easier to grasp the concept of place values in our decimal system. Let's explore the three types of blocks used in these models and how they relate to decimals!
First, we have the "ones" block, also known as the whole block. This is the largest piece in our set, usually shaped like a big cube. It represents one whole unit or the number 1. When we're working with decimals, this block is our starting point, showing us what a complete number looks like before we start breaking it down into smaller parts.
Next, we have the "tenths" block, which looks like a long, thin stick. If we lined up ten of these sticks next to each other, they would be the same size as one whole block. This is why we call them tenths each stick is one-tenth of the whole block. In decimal notation, a tenth is written as 0.1. These sticks help us understand the first place value to the right of the decimal point.
The smallest piece in our set is the "hundredths" block. This tiny square is so small that it takes 100 of them to equal one whole block. If you look closely, you'll see that ten hundredths blocks fit perfectly on top of one tenths stick. In decimal form, a hundredth is written as 0.01. These little squares represent the second place value to the right of the decimal point.
Now, let's see how these blocks work together to show decimals. Imagine we want to represent the number 1.23 using our base ten blocks. We would start with one whole block for the 1, then add two tenths sticks for the 0.2, and finally, three hundredths squares for the 0.03. By putting these pieces together, we can physically see and touch what 1.23 looks like!
These block models are great because they help us understand the relationship between different place values. We can easily see that ten hundredths make one tenth, and ten tenths make one whole. This visual representation makes it much easier to add, subtract, and compare decimals.
For example, if we wanted to add 0.5 and 0.25, we could use five tenths sticks for 0.5, and then two tenths sticks plus five hundredths squares for 0.25. By combining these, we can quickly see that the answer is 0.75, or seven tenths and five hundredths.
Base ten block models also help us understand why we line up decimal points when adding or subtracting. Each column of blocks represents a specific place value, just like in written decimal notation. This makes it clear why tenths should be added to tenths, and hundredths to hundredths.
As you practice with these blocks, you'll start to develop a strong mental image of how decimals work. This will make it easier to work with decimals even when you don't have the physical blocks in front of you. Remember, in our decimal system, each place value is ten times smaller than the one to its left. This pattern continues beyond hundredths into thousandths, ten-thousandths, and so on.
By using base ten block models, we can turn abstract decimal concepts into concrete, touchable objects. This hands-on approach makes learning about decimals much more engaging and helps build a solid foundation for more advanced math skills. So next time you're working with decimals, try imagining these colorful blocks it might just make your decimal adventures a whole lot more fun!
Regrouping in Decimal Addition
Regrouping in decimal addition is a fundamental concept in mathematics that builds upon the principles of whole number addition. This process involves understanding the relationship between different place values in our decimal system, particularly how smaller units combine to form larger ones. In decimal addition, we often need to regroup when working with hundredths and tenths, just as we do with ones, tens, and hundreds in whole number addition.
To visualize this concept, we can use base ten block models. These models provide a concrete representation of decimal values, making it easier to understand the regrouping process. In the decimal system, we have a crucial relationship: ten hundredths make one tenth, and ten tenths make one whole. This relationship is the foundation of regrouping in decimal addition.
Let's consider an example using base ten block models. Imagine we're adding 0.47 and 0.56. In our model, a large square represents one whole, a long rectangle represents one tenth, and a small square represents one hundredth. When we combine 7 hundredths from 0.47 and 6 hundredths from 0.56, we get 13 hundredths. However, we can't have more than 9 in the hundredths place, so we need to regroup.
In this regrouping process, we take 10 of these hundredths and combine them to form one tenth. Visually, we would replace 10 small squares (hundredths) with one long rectangle (tenth). This leaves us with 3 hundredths and an extra tenth. We then add this new tenth to the tenths column, where we already have 4 tenths from 0.47 and 5 tenths from 0.56. This gives us a total of 10 tenths in the tenths column.
Again, we can't have 10 in the tenths place, so we regroup once more. Ten tenths make one whole, so we replace our 10 long rectangles (tenths) with one large square (whole). This whole number is then carried over to the ones place. After this regrouping, we're left with 1 in the ones place, 0 in the tenths place, and 3 in the hundredths place, giving us the final answer of 1.03.
This process is similar to regrouping in whole number addition, where we might add 47 and 56. In that case, 7 ones and 6 ones give us 13 ones, which we regroup as 1 ten and 3 ones. The 1 ten is then added to the tens column, giving us 11 tens, which we again regroup as 1 hundred and 1 ten. The final result is 103, mirroring our decimal addition result but shifted two places to the left.
Understanding this parallel between whole number and decimal regrouping can reinforce the concept. In both cases, we're dealing with place value and the idea that when we have too many of one unit, we convert them into the next larger unit. The key difference is the size of the units we're working with hundredths, tenths, and ones in decimal addition, compared to ones, tens, and hundreds in whole number addition.
Mastering regrouping in decimal addition is crucial for more advanced mathematical operations. It forms the basis for understanding more complex calculations involving decimals, including subtraction, multiplication, and division. By visualizing the process using base ten block models and drawing parallels to whole number addition, students can develop a strong foundation in decimal operations, setting the stage for success in higher-level mathematics.
Adding Decimals with Base Ten Block Models
Adding decimals using base ten block models is an effective visual method to understand decimal addition. This step-by-step guide will walk you through the process, complete with two detailed examples to illustrate the concept.
Step-by-Step Instructions:
- Set up your base ten blocks:
- Flat square = 1 whole
- Long stick = 0.1 (one-tenth)
- Small cube = 0.01 (one-hundredth)
- Represent each decimal number using the appropriate blocks.
- Combine the blocks for both numbers.
- Regroup if necessary (10 small cubes = 1 long stick, 10 long sticks = 1 flat square).
- Count the final arrangement to get your answer.
Example 1: Adding 0.8 + 0.7
- Represent 0.8 with 8 long sticks.
- Represent 0.7 with 7 long sticks.
- Combine the blocks: You now have 15 long sticks.
- Regroup: 10 long sticks make 1 flat square (1 whole), leaving 5 long sticks.
- Final arrangement: 1 flat square and 5 long sticks = 1.5
Therefore, 0.8 + 0.7 = 1.5
Example 2: Adding 0.67 + 0.58 (More Complex)
- Represent 0.67:
- 6 long sticks (0.6)
- 7 small cubes (0.07)
- Represent 0.58:
- 5 long sticks (0.5)
- 8 small cubes (0.08)
- Combine the blocks:
- 11 long sticks
- 15 small cubes
- Regroup:
- 15 small cubes = 1 long stick + 5 small cubes
- Now we have 12 long sticks and 5 small cubes
- 12 long sticks = 1 flat square + 2 long sticks
- Final arrangement:
- 1 flat square (1 whole)
- 2 long sticks (0.2)
- 5 small cubes (0.05)
Therefore, 0.67 + 0.58 = 1.25
Key Points to Remember:
- Always align your blocks correctly, keeping tenths and hundredths separate.
- Regroup whenever you have 10 or more of one type of block.
- Practice with different combinations to become more comfortable with the process.
Using base ten block models for adding decimals provides a concrete, visual representation of abstract mathematical concepts. This method helps students understand place value and the regrouping process in decimal addition. By physically manipulating the blocks, learners can see how tenths combine to
Connecting Base Ten Models to Standard Algorithm
The process of adding with base ten block models and the standard algorithm for adding decimals are closely related, both relying on the fundamental principles of place value and decimal point alignment. Understanding this connection can greatly enhance a student's grasp of decimal addition and reinforce the logic behind the standard algorithm.
When using base ten block models, we represent whole numbers and decimals visually. Flats typically represent ones, rods represent tenths, and small cubes represent hundredths. The key to this method is organizing these blocks in columns according to their place value, with the decimal point serving as a clear divider between whole numbers and fractional parts.
Similarly, the standard algorithm for adding decimals emphasizes the critical importance of aligning decimal points and corresponding place values. This alignment ensures that we add digits of the same place value, just as we group similar blocks together in the model method.
Let's consider an example to illustrate this connection:
Adding 3.45 + 2.7 using base ten blocks:
- We would place 3 flats, 4 rods, and 5 small cubes to represent 3.45
- Next to it, we'd place 2 flats and 7 rods to represent 2.7
- Combining these, we get 5 flats, 11 rods, and 5 small cubes
- We then exchange 10 rods for 1 flat, resulting in 6 flats, 1 rod, and 5 small cubes
- This gives us the final answer of 6.15
Now, let's look at the same problem using the standard algorithm:
3.45
+ 2.70
------
6.15
Notice how we align the decimal points and add corresponding digits in each column, just as we grouped similar blocks in the model method. The '0' is added in the hundredths place of 2.7 to clarify the alignment, though it doesn't change the value.
Both methods emphasize the importance of place value and proper alignment. In the block model, we physically arrange blocks by their place value. In the standard algorithm, we write numbers in columns, aligning digits with the same place value. This alignment is crucial for accurate addition, as it ensures we're combining like terms.
The carry-over process in the standard algorithm (such as carrying the 1 from the tenths to the ones place in our example) mirrors the exchange of blocks in the model method (trading 10 rods for 1 flat). This reinforces the concept of regrouping in our base-ten number system.
By understanding the connection between these two methods, students can develop a deeper comprehension of decimal addition. The visual and tactile nature of base ten blocks provides a concrete foundation, while the standard algorithm offers an efficient, abstract representation of the same process. This dual approach can help solidify understanding and improve overall numeracy skills.
In conclusion, whether using base ten blocks or the standard algorithm, the key principles remain the same: align decimal points, respect place values, and perform operations column by column. This consistency across methods underscores the logical structure of our decimal system and provides multiple pathways for students to grasp and master decimal addition.
Common Mistakes and Tips for Adding Decimals
Adding decimals can be tricky for students, and several common mistakes often arise. Understanding these errors and learning strategies to avoid them is crucial for mastering decimal addition. Let's explore some frequent pitfalls and provide helpful tips to ensure accurate calculations.
1. Misaligning Decimal Points
One of the most common mistakes is misaligning decimal points when setting up the addition problem. Students may forget that decimal points must be lined up vertically for correct addition. For example:
Incorrect: 3.45
+1.2
To correct this, always emphasize the importance of aligning decimal points:
Correct: 3.45
+1.20
2. Forgetting to Regroup
Another frequent error occurs when students forget to regroup (carry) when the sum of a column exceeds 9. For instance:
Incorrect: 5.67
+2.58
-----
7.115
The correct solution involves regrouping:
Correct: 5.67
+2.58
-----
8.25
3. Ignoring Placeholder Zeros
Students often overlook the importance of placeholder zeros, leading to incorrect answers. For example:
Incorrect: 4.3
+2.15
-----
6.45
The correct approach is to add a placeholder zero:
Correct: 4.30
+2.15
-----
6.45
Tips and Strategies
- Use graph paper to help align decimal points vertically.
- Encourage students to add placeholder zeros to make all numbers have the same number of decimal places.
- Practice with block models to visualize decimal place values.
- Double-check answers by estimating and rounding to whole numbers.
Using Block Models
Block models can help students visualize decimal addition. For example, to add 1.23 + 0.45:
(1) (0.2) (0.03) + (0.4) (0.05) = (1) (0.6) (0.08) = 1.68
This visual representation helps students understand place value and regrouping in decimal addition.
Standard Algorithm Practice
While block models are helpful, students should also master the standard algorithm. Encourage them to follow these steps:
- Align decimal points vertically
- Add placeholder zeros if necessary
- Add each column from right to left
- Regroup when needed
- Place the decimal point in the answer directly below the aligned points
By addressing these common mistakes and implementing these strategies, students can significantly improve their decimal addition skills. Regular practice and visualization techniques will help reinforce correct methods and build confidence in working with decimals.
Practice Problems and Self-Assessment
To reinforce your understanding of adding decimals, let's dive into a set of practice problems. These exercises will help you apply your knowledge using both base ten block models and standard algorithms. Remember, self-assessment is key to mastering this skill, so we'll also provide guidance on how to check your work.
1. Using base ten block models, solve: 2.34 + 1.65
2. Apply the standard algorithm to find: 5.78 + 3.92
3. Combine 0.9 and 1.23 using both methods
4. Calculate 4.56 + 2.89 using the algorithm, then verify with blocks
5. Add 7.1 and 2.35 using blocks, then confirm with the algorithm
To self-assess your work, follow these steps:
- For base ten block models:
- Ensure you've correctly represented each decimal
- Check that you've combined like units (ones with ones, tenths with tenths, etc.)
- Verify any regrouping steps
- Count the final arrangement carefully
- For standard algorithm solutions:
- Double-check your column alignment
- Recount any carried numbers
- Perform the addition again from bottom to top
- Verify decimal point placement in the final answer
To further verify your answers, use block models to check algorithm solutions and vice versa. This cross-checking method reinforces your understanding and helps identify any discrepancies. Remember, block models provide a visual representation that can often reveal errors in your algorithmic approach.
Practice regularly with a variety of problems, gradually increasing in complexity. Start with simpler two-decimal additions before moving on to mixed whole numbers and decimals or problems involving more than two addends. As you gain confidence, challenge yourself with word problems that require decimal addition in real-world contexts.
By consistently applying these self-assessment techniques and verification methods, you'll not only improve your accuracy but also deepen your conceptual understanding of decimal addition. This solid foundation will serve you well as you progress to more advanced mathematical concepts.
Conclusion
In this lesson on adding decimals, we've covered several key points to enhance your understanding. We emphasized the crucial role of place values in decimal addition and explored the connection between base ten block models and the standard algorithm. Remember, aligning decimal points and understanding the value of each digit are essential for accurate calculations. Regular practice is vital to reinforce these concepts and improve your skills. Don't hesitate to revisit the introduction video if you need a refresher on any topic. To further engage with decimal addition, try solving real-world problems involving money or measurements. Challenge yourself with increasingly complex problems and explain your reasoning to others. By mastering decimal addition, you're building a strong foundation for more advanced mathematical concepts. Keep up the great work, and remember that each practice session brings you closer to becoming a decimal addition expert!
Introduction to Adding Decimals: How to Add Decimals with Base Ten (Block) Models
In this guide, we will explore how to add decimals using base ten block models. This method helps visualize the process of adding decimals and understanding the concept of place values.
Step 1: Understanding Base Ten Block Models
Base ten block models are a visual representation of numbers using blocks. Each block represents a different place value:
- Ones: Represented by a full block with 100 little squares.
- Tenths: Represented by a stick with 10 little squares, which is 10 times smaller than the ones place.
- Hundredths: Represented by a single little square, which is 10 times smaller than the tenths place.
Step 2: Reviewing Place Values
When using base ten block models, it's important to remember the relationship between place values:
- One whole (ones place) can be divided into 10 tenths.
- One tenth can be divided into 10 hundredths.
Step 3: Regrouping in Addition
Regrouping is a key concept in addition, especially when dealing with decimals. When the sum of a place value exceeds 9, we regroup to the next higher place value. For example:
- When adding 37 and 25, we add the ones place (7 + 5 = 12), write down 2, and carry over 1 to the tens place.
- Similarly, when adding decimals, if the sum of the tenths place exceeds 9, we regroup to the ones place.
Step 4: Adding Decimals Using Base Ten Block Models
Let's go through an example of adding decimals using base ten block models:
- Consider adding 0.8 and 0.7. In base ten blocks, this is represented by 8 tenths sticks and 7 tenths sticks.
- When we add these together, we get 15 tenths sticks. Since 15 is a double-digit number, we need to regroup.
- We take 10 of these tenths sticks and regroup them into 1 whole block, leaving us with 5 tenths sticks.
- Thus, 0.8 + 0.7 equals 1.5 (1 whole and 5 tenths).
Step 5: Another Example with Hundredths
Consider adding 1.7 (17 tenths) and 0.32 (32 hundredths):
- First, we count the tenths and hundredths separately. We have 17 tenths and 32 hundredths.
- We regroup the 17 tenths into 1 whole block and 7 tenths sticks.
- We regroup the 32 hundredths into 3 tenths sticks and 2 hundredths squares.
- Combining these, we get 1 whole block, 10 tenths sticks (which regroup into another whole block), and 2 hundredths squares.
- Thus, 1.7 + 0.32 equals 2.02 (2 wholes and 2 hundredths).
Step 6: Summary of Regrouping
To summarize the regrouping process:
- Ten hundredths can be regrouped into one tenth.
- Ten tenths can be regrouped into one whole.
- When adding decimals, always check if regrouping is needed to simplify the sum.
Step 7: Practice Problems
To reinforce your understanding, try adding the following decimals using base ten block models:
- 0.5 + 0.6
- 1.3 + 0.45
- 2.75 + 1.25
FAQs
-
Why is aligning decimal points important when adding decimals?
Aligning decimal points is crucial because it ensures that you're adding digits with the same place value. This prevents errors such as adding tenths to hundredths or ones to tenths. By lining up the decimal points vertically, you create a clear structure where each column represents a specific place value, making the addition process more accurate and easier to follow.
-
How do base ten block models help in understanding decimal addition?
Base ten block models provide a visual and tactile representation of decimals, making abstract concepts more concrete. They help students understand place value by representing ones, tenths, and hundredths as different-sized blocks. This visual aid makes it easier to see how numbers combine and regroup during addition, reinforcing the concept of carrying over in decimal addition.
-
What is regrouping in decimal addition, and why is it important?
Regrouping in decimal addition occurs when the sum of digits in a particular place value exceeds 9. It involves carrying over to the next place value to the left. For example, when adding 0.7 and 0.6, the sum is 1.3, requiring regrouping from tenths to ones. Understanding regrouping is crucial for accurate decimal addition and builds a foundation for more complex mathematical operations.
-
How can I check if my decimal addition is correct?
To verify your decimal addition, you can: 1. Recheck your alignment of decimal points. 2. Add the numbers from bottom to top as a double-check. 3. Use estimation by rounding to whole numbers to see if your answer is reasonable. 4. Utilize base ten block models to visually confirm your calculation. 5. Use a calculator to verify your result, but always try to understand the process rather than relying solely on technology.
-
What are some real-world applications of decimal addition?
Decimal addition is widely used in everyday life, including: 1. Financial calculations, such as balancing a checkbook or calculating expenses. 2. Cooking and baking when adjusting recipe measurements. 3. Construction and carpentry for precise measurements. 4. Scientific data analysis and reporting. 5. Sports statistics, like calculating batting averages in baseball. Understanding decimal addition is crucial for many practical applications and professional fields.
Prerequisite Topics
Understanding the fundamentals of mathematics is crucial when it comes to mastering more advanced concepts like adding decimals. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in basic arithmetic and number sense is essential for success in working with decimals.
Adding decimals is a fundamental skill in mathematics that builds upon several core concepts. Although we don't have explicit prerequisites to link to, let's explore some of the underlying knowledge that contributes to proficiency in this area.
First and foremost, a solid understanding of place value is crucial. When adding decimals, students must align the decimal points correctly, which requires recognizing the significance of each digit's position. This concept extends from whole numbers into the realm of fractions and decimals, emphasizing the importance of a strong number sense.
Additionally, familiarity with basic addition is a key component. The process of adding decimals follows the same principles as adding whole numbers, but with the added complexity of maintaining decimal point alignment. Students who are comfortable with addition algorithms for whole numbers will find it easier to adapt these skills to decimal operations.
Another important aspect is the ability to convert between fractions and decimals. While not directly required for adding decimals, this skill enhances overall understanding and flexibility when working with different number representations. It allows students to see the connections between various forms of numbers and strengthens their mathematical reasoning.
Understanding rounding and estimation is also beneficial when working with decimals. These skills help students check the reasonableness of their answers and develop a sense of the magnitude of decimal numbers. Being able to estimate sums quickly can serve as a valuable tool for catching errors and building confidence in decimal arithmetic.
Lastly, a grasp of basic number properties, such as the commutative and associative properties of addition, can be helpful. These properties apply to decimal addition just as they do to whole numbers, providing a conceptual framework that supports efficient mental math and problem-solving strategies.
While we don't have specific links to prerequisite topics, it's clear that a strong foundation in these fundamental areas of mathematics is essential for success in adding decimals. By ensuring a solid understanding of these underlying concepts, students can approach decimal addition with confidence and build upon this knowledge for more advanced mathematical topics in the future.

