Representing numbers: Ordinals
Topic Notes
In this lesson, we will learn:
- How to write ordinal numbers using numbers and superscripts
- How to write ordinal numbers using words and suffixes
- How to use ordinal numbers to understand order/ranking/position
Notes:
- Ordinal means Order
- Ordinal numbers answer the question “what place/rank/position”?
- Ordinal numbers are whole numbers only (no fractions nor decimals)
- Ordinal numbers follow similar rules to the way we write number word names
- The difference is that ordinals have special endings, or “suffixes”
- When you write ordinals as numbers, these endings are superscripts
- You write these letters smaller and write them above the normal line
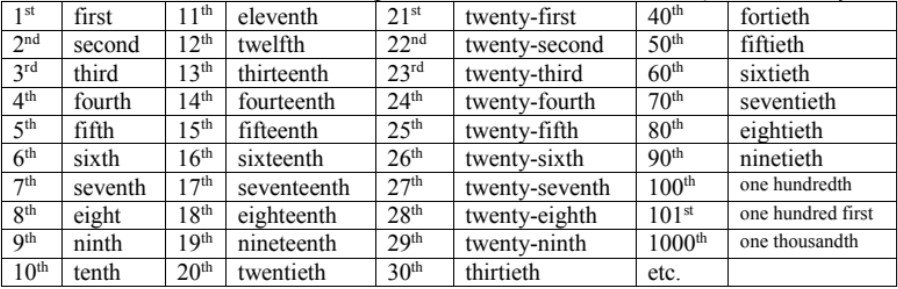
- i.e. 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, etc.
- When you write ordinals as words, most ordinal numbers end with “–th” except for numbers that end with 1, 2, or 3 (which use “–st”, “–nd”, and “–rd”, respectively)
- For multiples of ten from 20 to 90, they end with “–ieth”
- The ordinal 9th is spelled as “ninth” without the e (that is usually in nine)
- There are 3 types of numbers: Cardinal, Ordinal, and Nominal
- Cardinal means Counting (ex. there are 6 pool balls)
- Ordinal means Order (ex. the purple pool ball is in 4th place)
- Nominal means Name (ex. the green pool ball is labelled “14”)
- It’s important to know the difference between the word names for written ordinal numbers, written decimals, and written fractions:
- Ex. 200th is written as two hundredth
- Ex. is written as two-hundredths
- Ex. 0.02 is written as two hundredths
Introduction to Ordinal Numbers
Welcome to the fascinating world of ordinal numbers! These special numbers play a crucial role in mathematics, helping us understand the order and position of objects in a sequence. Ordinal numbers are used to describe the "nth" position, such as first, second, third, and so on. They're essential for organizing information, ranking, and establishing hierarchies in various mathematical and real-world applications. Our introduction video is designed to make this concept easy to grasp and fun to learn. As your virtual math tutor, I'm excited to guide you through this important topic. The video will cover the basics of ordinal numbers, their symbols, and how they differ from cardinal numbers. You'll see practical examples that demonstrate how ordinal numbers are used in everyday life, from sports rankings to scheduling events. By the end of this lesson, you'll have a solid foundation in ordinal numbers, setting you up for success in more advanced mathematical concepts.
Understanding Ordinal Numbers
Ordinal numbers are a fundamental concept in mathematics that play a crucial role in our everyday lives. Unlike cardinal numbers, which simply express quantity, ordinal numbers indicate position or rank within a sequence. This distinction is essential for understanding the order and hierarchy of items in various contexts.
To grasp the concept of ordinal numbers, let's consider a common scenario: a race. In a race, we use ordinal numbers to describe the finishing positions of participants. For example, the runner who crosses the finish line first is awarded "1st place," the next runner receives "2nd place," followed by "3rd place," and so on. These ordinal numbers clearly indicate the order in which the runners completed the race, providing a ranking system that goes beyond mere quantity.
Cardinal numbers, on the other hand, simply tell us how many of something there are. If we were to count the number of runners in the race, we would use cardinal numbers: one runner, two runners, three runners, and so forth. While cardinal numbers answer the question "How many?", ordinal numbers answer the question "Which position?" or "What order?"
The importance of order in ordinal numbers cannot be overstated. Consider a line of people waiting for a popular attraction. The person at the front of the line is in the "1st position," followed by the "2nd," "3rd," and subsequent positions. This ordering is crucial for maintaining fairness and organization. It ensures that people are served or admitted in the sequence they arrived, respecting the principle of "first come, first served."
Ordinal numbers are not limited to competitive scenarios or queues. They are used in various aspects of our lives, including:
- Dates: We use ordinal numbers to specify days of the month (1st, 2nd, 3rd, etc.).
- Education: Grade levels are often expressed as ordinal numbers (1st grade, 2nd grade, etc.).
- Royalty and leadership: Monarchs and popes are often referred to by their ordinal number (Elizabeth II, Pope John Paul II).
- Street addresses: Many street names include ordinal numbers (5th Avenue, 42nd Street).
The formation of ordinal numbers in English follows specific patterns. For numbers ending in 1, 2, or 3 (except 11, 12, and 13), we add "st," "nd," or "rd" respectively. For all other numbers, including 11, 12, and 13, we add "th." This system allows us to easily convert cardinal numbers into their ordinal counterparts: one becomes first, two becomes second, three becomes third, and so on.
Understanding the relationship between cardinal and ordinal numbers is crucial for mathematical literacy. While cardinal numbers focus on quantity, ordinal numbers provide context and structure to sequences and rankings. This distinction becomes particularly important in fields such as statistics, where both types of numbers are used to analyze and interpret data.
In conclusion, ordinal numbers are an essential component of our numerical system, providing a way to express order, rank, and position. Their ability to convey sequence and hierarchy makes them indispensable in various aspects of life, from competitive sports to everyday organization. By understanding the difference between ordinal and cardinal numbers, we gain a more comprehensive grasp of mathematical concepts and their practical applications in the world around us.
Writing and Reading Ordinal Numbers
Ordinal numbers are essential in everyday communication, indicating position or order in a sequence. Understanding how to write and read ordinal numbers correctly, both numerically and in words, is crucial for effective communication. This guide will explore the rules for forming ordinals, including special cases, and provide examples and practice exercises to reinforce your understanding.
Numerical Representation of Ordinal Numbers
When writing ordinal numbers numerically, we use suffixes added to the cardinal number. The most common ordinal suffixes are:
- -st for numbers ending in 1 (except 11)
- -nd for numbers ending in 2 (except 12)
- -rd for numbers ending in 3 (except 13)
- -th for all other numbers
Examples:
- 1st (first)
- 2nd (second)
- 3rd (third)
- 4th (fourth)
- 11th (eleventh)
- 21st (twenty-first)
- 32nd (thirty-second)
- 43rd (forty-third)
- 100th (one hundredth)
Word Representation of Ordinal Numbers
When writing ordinal numbers in words, we follow specific rules:
- For numbers 1-19, use unique words: first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh, twelfth, thirteenth, fourteenth, fifteenth, sixteenth, seventeenth, eighteenth, nineteenth.
- For multiples of 10 (20, 30, 40, etc.), replace the 'y' with 'ieth': twentieth, thirtieth, fortieth, fiftieth, sixtieth, seventieth, eightieth, ninetieth.
- For compound numbers, only the last word is changed to its ordinal form: twenty-first, thirty-second, forty-third, etc.
- For 100 and above, use the cardinal number followed by the ordinal form of the last digit: one hundred and first, two hundred and second, etc.
Special Cases and Exceptions
Some ordinal numbers have unique spellings that don't follow the general rules:
- 'Fifth' instead of 'fiveth'
- 'Twelfth' instead of 'twelveth'
- 'Eighth' retains the 'ht' from 'eight'
- 'Ninth' drops the 'e' from 'nine'
Practice Exercises
To reinforce your understanding of ordinal numbers, try these exercises:
- Write the following numbers as ordinals both numerically and in words:
- 23
- 55
- 101
- 42
- Convert these word ordinals to their numerical representation:
- Sixty-seventh
- One hundred and fifth
- Thirty-third
- Ninety-ninth
- Identify and correct any errors in these ordinal numbers:
- 22th
- Fourty-third
- 13rd
- One hundred and oneth
- If today is the 7th of the month, what ordinal number would represent the day three weeks from now?
- In a race with 50 runners, John finished 23rd. How many runners finished after him?
- If you live on the 6th floor of an apartment building with 10 floors, how many floors are above you?
- In a class ranking, Sarah is 5th from the top in a class of 28 students. What ordinal number would represent her position if counted from the bottom?
- If the 1st day of a month is a Tuesday, what day of the week will the 22nd be?
- Cardinal numbers can be converted to ordinal numbers (e.g., 1 becomes first, 2 becomes second).
- Ordinal numbers imply a sequence, while cardinal numbers don't necessarily do so.
- Nominal numbers may use digits but don't follow mathematical rules like the other two types.
- It helps in clear communication and avoiding misunderstandings.
- It's crucial for data analysis and statistical interpretation.
- It's essential in programming and database management.
- It aids in problem-solving and logical reasoning.
- Identify the number type:
- "I live on 42nd Street." (Ordinal)
- "There are 50 states in the USA." (Cardinal)
- "My license plate is XYZ-789." (Nominal)
- Convert cardinal to ordinal:
- 5 Fifth
- 23 Twenty-third
- 101 One hundred and first
- Use each number type in a sentence:
- Cardinal: "I bought 12 eggs at the store."
- Ordinal: "This is my 5th attempt at solving the puzzle."
- Nominal: "Dial extension 4567 to reach customer service."
- ω: The first transfinite ordinal, representing the order type of the natural numbers
- ω+1: The next ordinal after ω, which can be thought of as "infinity plus one"
- ω·2: Represents two copies of ω placed end to end
- ω^2: The order type of ω copies of ω
- ε: The smallest ordinal α such that ω^α = α
- Proof theory: Ordinals are used to measure the complexity of proofs and the strength of mathematical systems.
- Computer science: Ordinals help in analyzing the termination of algorithms and in defining hierarchies of computational complexity.
- Set theory: Ordinals are fundamental in constructing and studying various set-theoretic models.
- Topology: Ordinals play a role in describing certain topological spaces and their properties.
- Describe the order type of the set of integers (..., -2, -1, 0, 1, 2, ...) using ordinals.
- What is the ordinal that represents the order type of the rational numbers between 0 and 1?
- Explain the difference between ω+ω and ω·2.
- Can you think of a real-world analogy to help understand the concept of transfinite ordinals?
Using Ordinal Numbers in Context
Ordinal numbers play a crucial role in our everyday lives, helping us organize and communicate information in various contexts. From marking important dates to ranking athletes in competitions, these numbers are essential for expressing order and position. Let's explore some real-life applications of ordinal numbers and how they're used in everyday language and situations.
Dates and Calendars
One of the most common uses of ordinal numbers is in expressing dates. We use ordinals to specify the day of the month, such as "January 1st," "February 2nd," or "March 3rd." This application helps us distinguish between days and communicate specific dates clearly. For example, we might say, "The concert is on the 15th of July," or "Her birthday falls on the 22nd of August."
Sports Rankings
In the world of sports, ordinal numbers are essential for indicating rankings and positions. Athletes and teams are often described using ordinals to show their standing in competitions. For instance, we might hear announcements like "She finished in 1st place in the marathon," or "The team is currently ranked 3rd in the league." Ordinals are also used in describing race positions: "He's in 2nd place, gaining on the leader!"
Academic Standings
Educational institutions frequently use ordinal numbers to express academic performance and class rankings. Students might be described as "1st in their class" or "ranked 5th out of 100 students." Ordinals are also used in describing grade levels, such as "3rd grade" or "11th grade." Additionally, academic competitions often use ordinals to announce winners, like "The 2nd place in the science fair goes to..."
Everyday Language
Beyond these specific contexts, ordinal numbers are woven into our everyday language in numerous ways. We use them to describe the order of events ("This is the 3rd time I've reminded you"), to indicate floor levels in buildings ("My office is on the 4th floor"), or to express preferences ("This is my 2nd favorite book"). They're also common in describing familial relationships ("She's my 1st cousin") and in naming monarchs or popes ("Elizabeth II" or "Pope John Paul II").
Other Applications
Ordinal numbers find their way into many other areas of life as well. In product versions or editions, we often see labels like "2nd generation iPhone" or "3rd edition of the textbook." In music, ordinals are used to describe chord inversions ("1st inversion of C major"). Even in cooking, recipes might call for steps like "2nd rise of the dough" or "3rd layer of the cake."
Practice Problems
To help reinforce your understanding of ordinal numbers in context, try these practice problems:
By practicing with these real-life scenarios, you'll become more comfortable using ordinal numbers in various contexts. Remember, ordinal numbers are all around us, helping to bring order and clarity to many aspects of our daily lives. Whether you're marking important dates on your calendar, following your favorite sports team's rankings, or tracking your academic progress, ordinal numbers provide a concise and universally understood way to express order and position.
Comparing Ordinal, Cardinal, and Nominal Numbers
Understanding the differences between ordinal, cardinal, and nominal numbers is crucial in mathematics and everyday life. These number types serve distinct purposes and are used in various contexts. Let's explore each type, their relationships, and why it's important to distinguish between them.
Cardinal Numbers
Cardinal numbers are the most familiar type, used for counting and expressing quantity. They answer the question "How many?" Examples include 1, 2, 3, 4, and so on. We use cardinal numbers in everyday situations like counting objects, expressing ages, or measuring quantities. For instance, "I have three apples" or "There are 24 hours in a day."
Ordinal Numbers
Ordinal numbers, on the other hand, indicate position or order in a sequence. They answer the question "Which position?" Examples include first, second, third, fourth, etc. We use ordinal numbers to describe rankings, sequences, or positions. For example, "She finished in first place" or "This is the third time I've explained this concept."
Nominal Numbers
Nominal numbers, also known as identificational numbers, are used for identification or labeling purposes. They don't represent quantity or order but serve as names or labels. Examples include phone numbers, ZIP codes, or player jersey numbers. For instance, "My phone number is 555-1234" or "The product code is A-7890."
Relationships and Distinctions
While these number types are related, they serve different purposes:
Understanding these distinctions is important because:
Practice Exercises
To reinforce your understanding, try these exercises:
By mastering the differences between ordinal, cardinal, and nominal numbers, you'll enhance your mathematical understanding and improve your ability to communicate precisely in various contexts. Whether you're analyzing data, programming, or simply navigating daily life, recognizing these number types will prove invaluable. Practice identifying and using each type regularly to reinforce your skills and deepen your appreciation for the nuanced ways we use numbers in our world.
Advanced Concepts in Ordinal Numbers
As we delve deeper into the world of ordinal numbers, we encounter fascinating concepts that extend beyond everyday counting. In this section, we'll explore how ordinal numbers play a crucial role in set theory and introduce the mind-bending idea of transfinite ordinals. These advanced concepts open up new realms of mathematical thinking and have important applications in various fields.
Ordinal Numbers in Set Theory
In set theory, ordinal numbers are used to describe the order type of well-ordered sets. A well-ordered set is a set with a total order where every non-empty subset has a least element. Ordinals provide a way to measure and compare the "size" of these ordered sets, even when dealing with infinite sets.
For example, consider the set of natural numbers {0, 1, 2, 3, ...}. This set has an order type represented by the ordinal ω (omega), which is the first transfinite ordinal. We can then construct larger ordinals by continuing the sequence: ω+1, ω+2, ..., ω+ω (which is also written as ω·2), and so on.
Transfinite Ordinals
Transfinite ordinals are ordinal numbers that go beyond the finite. They allow us to extend our counting system into the infinite, providing a structured way to think about different sizes of infinity. Some key transfinite ordinals include:
These transfinite ordinals allow mathematicians to work with and compare different infinite sets, leading to profound insights in set theory and other areas of mathematics.
Applications and Importance
The study of ordinal numbers and their properties has far-reaching implications in mathematics and computer science. Some applications include:
Exercises for Understanding
To help grasp these advanced concepts, try the following exercises:
As you explore these advanced concepts, remember that ordinal numbers provide a powerful tool for understanding and working with ordered structures, both finite and infinite. They challenge our intuitions about numbers and infinity, pushing the boundaries of mathematical thought. By mastering these ideas, you'll gain a deeper appreciation for the elegance and complexity of mathematics, and open doors to further exploration in advanced mathematical fields.
Conclusion
In summary, this article has covered the essential aspects of ordinal numbers, providing a comprehensive understanding of their usage and importance. The key points discussed include the definition of ordinal numbers, their role in indicating position or order, and common examples in everyday life. The introduction video served as a crucial tool in helping students grasp this fundamental mathematical concept. We encourage students to actively practice using ordinal numbers in their daily routines, such as describing the order of events or listing items. This hands-on approach will reinforce their understanding and improve their fluency with ordinals. Furthermore, we recommend exploring related mathematical concepts to broaden their knowledge base. By mastering ordinal numbers, students lay a solid foundation for more advanced mathematical topics and enhance their overall numerical literacy. Remember, consistent practice and curiosity are key to excelling in mathematics and applying these concepts effectively in real-world scenarios.
Introduction to Ordinal Numbers: What are ordinal numbers?
Ordinal numbers are a type of number that indicates the position or order of something in a list. They are different from cardinal numbers, which represent quantity. Ordinal numbers are used to answer questions like "What place?", "What rank?", or "What position?" in a sequence.
Step 1: Understanding the Concept of Ordinal Numbers
Ordinal numbers are used to describe the order of items in a list. For example, in a race, you might ask, "What place did the red car finish in?" The answer could be "first place," "second place," or "third place." This concept of order is central to understanding ordinal numbers. They help us determine the position of an item in a sequence, such as first, second, third, and so on.
Step 2: Recognizing Ordinal Numbers
Ordinal numbers are similar to cardinal numbers but with a special suffix. For example, the number 1 becomes "1st," 2 becomes "2nd," and 3 becomes "3rd." These suffixes (st, nd, rd, th) are what distinguish ordinal numbers from cardinal numbers. Ordinal numbers are typically whole numbers and do not include fractions or decimals. For instance, you cannot have a "1.5th" place in a race.
Step 3: Writing Ordinal Numbers
There are two main ways to write ordinal numbers: using letters or using numbers with a suffix. For example, "first" can be written as "1st," "second" as "2nd," and "third" as "3rd." These suffixes are essential in identifying ordinal numbers. When writing ordinal numbers, it is important to include the correct suffix to indicate the order or position.
Step 4: Examples of Ordinal Numbers
Let's look at some examples to better understand ordinal numbers. Consider the following list: 18th, 56, 23rd, and 4.9. Among these, "18th" and "23rd" are ordinal numbers because they have the suffixes "th" and "rd," respectively. The number "56" is a cardinal number because it lacks a suffix, and "4.9" is not an ordinal number because it is a decimal.
Step 5: Identifying Ordinal Numbers in Context
Ordinal numbers are often used in various contexts, such as ranking, positions in a lineup, and places in a race. For example, in a school race, you might say, "She finished in 23rd place." This indicates her position in the race. Similarly, in a lineup, you might refer to the "first position," "second position," or "third position." These examples illustrate how ordinal numbers are used to describe order and position.
Step 6: Special Suffixes for Ordinal Numbers
The suffixes used in ordinal numbers are crucial in distinguishing them from other types of numbers. The most common suffixes are "st" for first, "nd" for second, "rd" for third, and "th" for other numbers like fourth, fifth, sixth, and so on. These suffixes are added to the base number to form the ordinal number. For example, "21" becomes "21st," "32" becomes "32nd," and "43" becomes "43rd."
Step 7: Summary of Ordinal Numbers
In summary, ordinal numbers are used to indicate the order or position of items in a list. They are similar to cardinal numbers but include special suffixes to denote their order. Ordinal numbers are typically whole numbers and do not include fractions or decimals. Understanding and recognizing ordinal numbers is essential in various contexts, such as ranking, positions in a lineup, and places in a race.
FAQs
-
What is the difference between cardinal and ordinal numbers?
Cardinal numbers express quantity (how many), while ordinal numbers indicate position or order. For example, "three" is a cardinal number, while "third" is its ordinal counterpart.
-
How do you write ordinal numbers?
Ordinal numbers are typically written with suffixes: -st (1st), -nd (2nd), -rd (3rd), and -th (4th, 5th, etc.). For numbers 11-13, always use -th. In words, use "first," "second," "third," and so on.
-
What are some common uses of ordinal numbers in everyday life?
Ordinal numbers are used in dates (March 1st), rankings (1st place), floor numbers (3rd floor), monarchs' names (Elizabeth II), and grade levels (5th grade), among others.
-
How do ordinal numbers work with larger numbers?
For compound numbers, only the last word becomes ordinal. For example, 21st is "twenty-first," 42nd is "forty-second," and 103rd is "one hundred and third."
-
What are transfinite ordinals?
Transfinite ordinals are ordinal numbers that extend beyond finite numbers, used in set theory to describe infinite ordered sets. The first transfinite ordinal is typically denoted as ω (omega), representing the order type of natural numbers.
Prerequisite Topics
Before delving into the fascinating world of representing numbers as ordinals, it's crucial to have a solid foundation in certain mathematical concepts. One key prerequisite topic that plays a significant role in understanding ordinal numbers is Greatest Common Factors (GCF). While it might not seem immediately apparent, the principles behind GCF contribute to a deeper comprehension of ordinal numbers and their applications.
Understanding Greatest Common Factors helps students develop a strong sense of number relationships and divisibility, which are fundamental concepts in mathematics. This knowledge forms a crucial stepping stone towards grasping the concept of ordinal numbers. Ordinals, which represent the position or order of elements in a sequence, rely on a clear understanding of how numbers relate to one another and how they can be arranged in a specific order.
The connection between GCF and ordinal numbers becomes more evident when we consider the practical applications of ordinal numbers. For instance, when organizing data or creating ranked lists, the ability to find common factors can be incredibly useful. This skill allows students to group and categorize items more effectively, which is a common use case for ordinal numbers in real-world scenarios.
Moreover, the logical thinking and problem-solving skills developed while studying Greatest Common Factors transfer directly to working with ordinal numbers. Both concepts require students to think systematically about numbers and their relationships. This analytical approach is essential when dealing with ordinal numbers, especially in more complex mathematical operations or when applying them to real-life situations.
Another aspect where the knowledge of GCF proves beneficial is in understanding the divisibility rules, which can be helpful when working with large ordinal numbers. Being able to quickly determine factors and multiples can significantly enhance a student's ability to work efficiently with ordinal representations of numbers, particularly in advanced mathematical contexts.
Furthermore, the concept of GCF introduces students to the idea of finding commonalities between numbers, which is analogous to understanding the relative positions represented by ordinal numbers. This parallel thinking helps in grasping the sequential nature of ordinals and how they relate to one another in a series.
In conclusion, while Greatest Common Factors might not directly deal with ordinal numbers, it provides a crucial foundation for understanding number relationships, order, and mathematical reasoning. These skills are indispensable when learning about representing numbers as ordinals. By mastering GCF, students equip themselves with the necessary tools to tackle more advanced concepts in number theory and representation, including the fascinating world of ordinal numbers.

