Basics of symmetry
Topic Notes
In this lesson, we will learn:
- How to identify symmetrical vs. asymmetrical shapes or pictures
- How to check symmetry lines with the folding method or mirror test method
Notes:
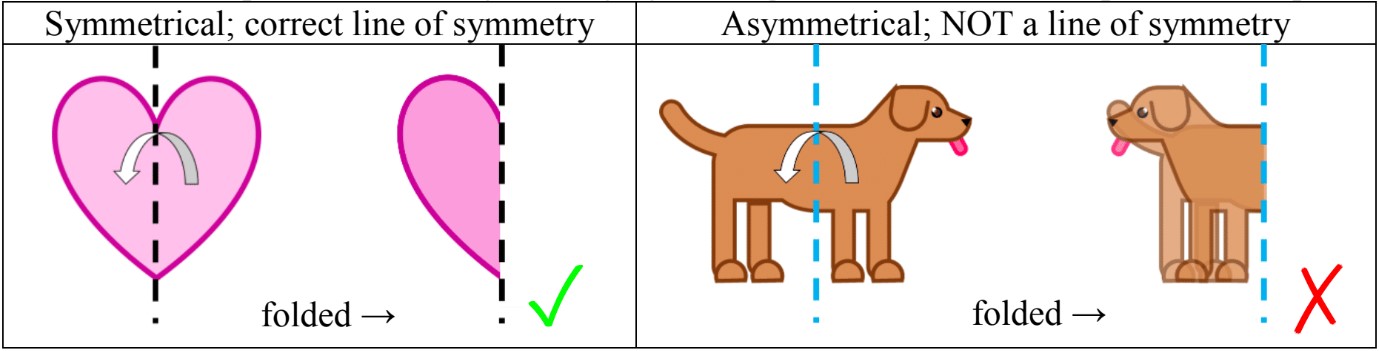
- A "symmetrical" shape is made up of exact same parts facing each other
- A line of symmetry divides a symmetrical shape into 2 congruent parts
- If the shape is not symmetrical it is "asymmetrical"

- Check if a shape has a line of symmetry by folding it in half to see if the parts match up
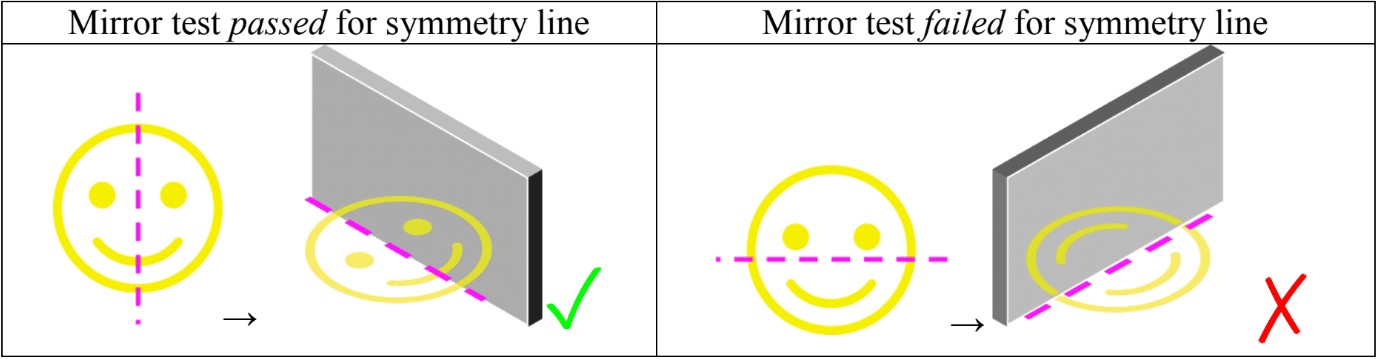
- or using a mirror test: laying the picture/shape flat and putting a mirror on a possible symmetry line to see if the mirrored image matches with the original
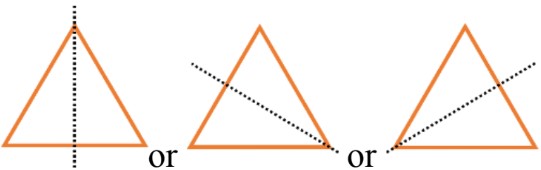
- Some shapes have more than one line of symmetry. Regular polygons have the same number of symmetry lines as number of sides
- some words (alphabet letters) and numbers also have symmetry:
Ex. triangles = 3 sides = 3 symmetry lines

Introduction to Symmetry
Symmetry is a fundamental concept in mathematics that plays a crucial role in various fields. Our introduction video serves as an essential starting point for understanding the basics of symmetry. This lesson will explore the fascinating world of symmetrical shapes, teaching you how to identify them and check for symmetry lines. We'll delve into the significance of symmetry in everyday objects, highlighting its prevalence in nature, architecture, and design. By mastering these concepts, you'll develop a keen eye for recognizing symmetrical patterns in the world around you. From simple geometric shapes to complex structures, symmetry is everywhere. This foundational knowledge will not only enhance your mathematical skills but also deepen your appreciation for the beauty and order in our universe. Join us as we uncover the secrets of symmetry and its applications in mathematics and beyond.
Understanding Symmetrical and Asymmetrical Shapes
Symmetrical and asymmetrical shapes are fundamental concepts in geometry and design. Understanding these concepts can help us appreciate the balance and beauty in both natural and man-made objects. Let's explore the definitions, characteristics, and examples of symmetrical and asymmetrical shapes.
Symmetrical Shapes
A symmetrical shape is one that can be divided into two identical halves. The imaginary line that divides the shape is called the line of symmetry. When you fold a symmetrical shape along its line of symmetry, the two halves match perfectly, creating congruent parts. This property gives symmetrical shapes a sense of balance and harmony.
Line of Symmetry
The line of symmetry is a crucial concept in understanding symmetrical shapes. It acts as a mirror, reflecting one half of the shape to create the other half. A shape can have one or multiple lines of symmetry. For example, a square has four lines of symmetry, while an equilateral triangle has three.
Examples of Symmetrical Shapes
Many common shapes and objects exhibit symmetry:
- Heart shape: The classic heart shape has a vertical line of symmetry down its center.
- Chevron shape: This V-shaped pattern has both vertical and horizontal lines of symmetry.
- Circle: A perfect circle has infinite lines of symmetry passing through its center.
- Human face: Most human faces have approximate vertical symmetry.
Identifying Symmetry in Everyday Objects
Symmetry is abundant in our surroundings. To identify symmetry in everyday objects, look for:
- Mirror images: If you can imagine a mirror placed on an object and it looks the same on both sides, it's likely symmetrical.
- Folding: Visualize folding the object in half. If the halves align perfectly, it's symmetrical.
- Rotational symmetry: Some objects look the same when rotated, like a snowflake or a star.
Asymmetrical Shapes
In contrast to symmetrical shapes, asymmetrical shapes lack a line of symmetry. These shapes cannot be divided into two identical halves that mirror each other. Asymmetrical shapes are often more dynamic and can create visual interest through their lack of perfect balance.
Characteristics of Asymmetrical Shapes
Asymmetrical shapes have several defining features:
- No line of symmetry: There is no way to divide the shape into two identical halves.
- Uneven distribution: Elements within the shape are not evenly distributed or balanced.
- Unique sides or angles: Each side or angle of the shape may be different from the others.
Examples of Asymmetrical Shapes
Asymmetry is also common in nature and design:
- Organic shapes: Many natural forms like leaves, clouds, or rock formations are asymmetrical.
- Modern architecture: Some contemporary buildings intentionally use asymmetry for visual impact.
- Abstract art: Many artists use asymmetrical compositions to create dynamic and engaging works.
Why Asymmetrical Shapes Lack Symmetry
Asymmetrical shapes lack symmetry for various reasons:
- Natural growth patterns: In nature, asymmetry often results from adaptive growth or environmental factors.
- Functional design: Some objects are asymmetrical to serve specific purposes or improve functionality.
- Artistic expression: Designers and artists may choose asymmetry to evoke certain emotions
Methods for Checking Symmetry
Symmetry is a fundamental concept in mathematics and art, and there are two primary methods for checking symmetry: the folding method and the mirror test method. Understanding these techniques can help you identify symmetrical shapes and objects in various contexts.
The Folding Method
The folding method is a hands-on approach to checking symmetry. Here's how to use it:
- Start with a paper cutout or drawing of the shape you want to check.
- Fold the paper along the suspected line of symmetry.
- Press the folded halves together.
- Hold the folded paper up to a light source.
- If the edges align perfectly and no light shines through, the shape is symmetrical.
For example, if you draw a smiley face on paper and fold it vertically down the center, the two halves should match up perfectly if it's symmetrical.
The Mirror Test Method
The mirror test method uses reflection to check for symmetry:
- Place a small mirror perpendicular to the surface, along the suspected line of symmetry.
- Look at the reflection in the mirror alongside the original half of the object.
- If the reflection completes the object seamlessly, it's symmetrical.
This method works well for three-dimensional objects. For instance, you could use it to check the symmetry of an eyeball model by placing the mirror along its center.
Applying These Methods to Various Shapes and Objects
Both the folding method and mirror test can be applied to a wide range of shapes and objects:
- Geometric shapes: Triangles, squares, circles, etc.
- Letters and numbers: Many letters like 'A', 'H', 'O', and numbers like '8' have symmetry.
- Natural objects: Leaves, flowers, and some animals exhibit symmetry.
- Architecture: Buildings and structures often incorporate symmetrical designs.
- Everyday items: Many household objects, from vases to furniture, can be checked for symmetry.
Common Mistakes When Checking for Symmetry
When checking for symmetry, be aware of these common pitfalls:
- Assuming all shapes have symmetry: Not every shape or object is symmetrical.
- Overlooking multiple lines of symmetry: Some shapes, like a square, have more than one line of symmetry.
- Confusing rotational symmetry with line symmetry: An object may look the same when rotated but not have line symmetry.
- Ignoring small details: Tiny imperfections can break symmetry, so be thorough in your examination.
- Not considering 3D symmetry: Remember that symmetry can exist in three dimensions, not just on a flat plane.
Mastering these methods for checking symmetry can enhance your understanding of geometry and improve your ability to analyze shapes and designs. Whether you're a student studying mathematics, an artist creating balanced compositions, or simply curious about the world around you, these techniques offer valuable insights into the symmetrical nature of many objects we encounter daily.
Practice using both the folding method and mirror test on various objects to hone your skills. Start with simple shapes like the smiley face or basic geometric forms, then progress to more complex objects. Remember that symmetry isn't always perfect in nature or man-made objects, so use these methods as guidelines rather than strict rules. By regularly applying these techniques, you'll develop a keen eye for symmetry and asymmetry in your environment, enriching your perception of the world's geometric patterns and designs.
Symmetry in Regular Polygons
Symmetry is a fundamental concept in geometry, and it plays a crucial role in understanding the properties of regular polygons. A regular polygon is a shape with equal sides and equal angles, and one of its most fascinating characteristics is its symmetry. In this exploration of symmetry in regular polygons, we'll delve into the relationship between a polygon's sides and its lines of symmetry, using the equilateral triangle as a prime example.
One of the key features of regular polygons is that they possess the same number of symmetry lines as they have sides. This property is what gives regular polygons their perfect balance and aesthetic appeal. To understand this concept better, let's consider the equilateral triangle, which serves as an excellent illustration of multiple lines of symmetry in a regular polygon.
An equilateral triangle, with its three equal sides and three equal angles, demonstrates three distinct lines of symmetry. These lines can be drawn from each vertex to the midpoint of the opposite side, effectively dividing the triangle into two identical halves. This means that if you were to fold the triangle along any of these lines, the two halves would perfectly overlap, showcasing the polygon's symmetrical nature.
The concept of symmetry is intrinsically linked to the properties of regular polygons. For instance, the presence of multiple lines of symmetry ensures that all sides of a regular polygon are equal in length, and all interior angles are congruent. This symmetry also contributes to the polygon's rotational symmetry, allowing it to be rotated a certain number of degrees and still appear identical to its original position.
To further illustrate the relationship between the number of sides and symmetry lines in regular polygons, consider the following table:
| Regular Polygon | Number of Sides | Number of Symmetry Lines |
|---|---|---|
| Equilateral Triangle | 3 | 3 |
| Square | 4 | 4 |
| Regular Pentagon | 5 | 5 |
| Regular Hexagon | 6 | 6 |
| Regular Octagon | 8 | 8 |
As we can see from this table, the pattern of symmetry lines matching the number of sides holds true for all regular polygons. This consistency is what makes regular polygons so unique and mathematically interesting. The more sides a regular polygon has, the more lines of symmetry it possesses, leading to increasingly complex symmetrical patterns.
Understanding symmetry in regular polygons is not just a matter of mathematical curiosity; it has practical applications in various fields. Architects and designers often use the principles of symmetry found in regular polygons to create balanced and aesthetically pleasing structures. In nature, many organisms and crystals exhibit symmetry similar to that found in regular polygons, demonstrating the fundamental importance of these geometric principles in the natural world.
In conclusion, the concept of symmetry in regular polygons, exemplified by the equilateral triangle with its multiple lines of symmetry, is a fascinating aspect of geometry. The direct correlation between the number of sides and symmetry lines in regular polygons underscores the elegant simplicity and balance inherent in these shapes. By understanding these properties, we gain deeper insights into the mathematical beauty that surrounds us and the principles that govern geometric forms.
Symmetry in Letters, Numbers, and Words
Symmetry is a fascinating concept that plays a significant role in the world of letters, numbers, and words. It's a principle that not only adds aesthetic appeal but also contributes to readability and recognition. In this exploration, we'll delve into the various forms of symmetry found in our alphabet, numerical system, and even complete words.
Let's start with alphabet letters. Many letters in the English alphabet exhibit symmetry, either horizontally or vertically. For instance, the letter 'A' has vertical symmetry, meaning if you draw a line down the middle, both halves mirror each other. Similarly, 'H', 'I', 'M', 'O', 'T', 'U', 'V', 'W', 'X', and 'Y' all display vertical symmetry. On the other hand, 'B', 'C', 'D', 'E', and 'K' showcase horizontal symmetry, where the top half mirrors the bottom half.
Numbers also demonstrate symmetry. The digits '0', '3', and '8' have both horizontal and vertical symmetry, while '1' has vertical symmetry. Interestingly, when given half of a symmetrical letter or number, one can easily complete the shape by mirroring the given half. This principle is often used in puzzles and educational activities to enhance spatial awareness and pattern recognition skills.
Moving on to words, we find some intriguing examples of symmetry. The word 'DECK' is an excellent illustration of rotational symmetry in words in typography. When written in capital letters, 'DECK' appears the same when flipped upside down. This type of symmetry is also known as rotational symmetry in words. Another fascinating example is the word 'MATH'. When written in a specific stylized font, 'MATH' exhibits vertical symmetry, with each letter mirroring itself across a central vertical axis.
However, not all letters and numbers are symmetrical. Asymmetrical letters include 'F', 'G', 'J', 'L', 'N', 'P', 'Q', 'R', 'S', and 'Z'. These letters lack a clear line of symmetry either vertically or horizontally. An interesting example of an asymmetrical word is 'SNUG'. None of its letters exhibit symmetry, making it a completely asymmetrical word.
The concept of symmetry in typography and design has numerous practical applications. In logo design, symmetrical elements often create a sense of balance and professionalism. Many well-known brands utilize symmetry in their logos to enhance recognition and memorability. In web design, symmetrical layouts can provide a clean, organized appearance that's pleasing to the eye and easy to navigate.
Typography designers often use symmetry to create fonts that are both aesthetically pleasing and highly readable. Symmetrical letterforms can contribute to the overall harmony of a text, making it easier for readers to process information quickly. This is particularly important in signage and wayfinding systems, where clarity and quick comprehension are crucial.
In the world of art and calligraphy, symmetry plays a significant role in creating visually striking compositions. Artists and calligraphers often use the principles of symmetry to balance their work and guide the viewer's eye across the piece. Some calligraphic styles, such as certain forms of Arabic calligraphy, heavily rely on symmetry to create intricate and beautiful designs.
Interestingly, our brains are naturally drawn to symmetry. Studies have shown that humans tend to find symmetrical faces more attractive, and this preference for symmetry extends to other areas of visual perception. This innate appreciation for symmetry is one reason why it's so effective in design and typography.
In conclusion, symmetry in letters, numbers, and words is more than just a visual curiosity. It's a powerful tool in design, typography, and communication. From the simple elegance of symmetrical letters to the clever use of symmetry in word design, this principle continues to fascinate and inspire. Whether you're a designer, artist, or simply someone who appreciates the beauty of language and numbers, understanding symmetry can enhance your appreciation of the world around you. So next time you're reading a sign, looking at a logo, or even just writing your name, take a moment to notice
Real-World Applications of Symmetry
Symmetry plays a crucial role in various fields, including art, architecture, nature, and science. This fundamental concept has captivated humans for centuries, influencing our perception of beauty and order in the world around us. In art, symmetry is often used to create visually pleasing compositions and evoke a sense of balance. Artists throughout history have employed symmetrical patterns in their works to achieve harmony and aesthetic appeal.
In architecture, symmetry is a cornerstone of design, evident in iconic structures worldwide. From ancient Greek temples to modern skyscrapers, architects have utilized symmetrical elements to create visually striking and structurally sound buildings. The Taj Mahal in India and the United States Capitol building are prime examples of how symmetry can enhance the grandeur and impact of architectural marvels.
Nature abounds with symmetrical patterns, showcasing the inherent beauty of mathematical precision. Butterflies, with their mirrored wing patterns, exemplify bilateral symmetry. Snowflakes, each unique yet perfectly symmetrical, demonstrate radial symmetry. These natural wonders have inspired countless artists, designers, and scientists throughout history.
In the realm of science, symmetry is a fundamental concept that underpins many theories and discoveries. From the molecular structure of crystals to the laws of physics, symmetry helps scientists understand and explain complex phenomena. The concept of symmetry breaking has led to groundbreaking insights in particle physics and cosmology.
Man-made structures and designs often incorporate symmetry to achieve visual appeal and functionality. Corporate logos, such as those of Apple or Mercedes-Benz, utilize symmetry to create memorable and balanced designs. In product design, symmetry can enhance usability and aesthetics, making objects more intuitive and pleasing to the eye.
Understanding symmetry can be a powerful tool in problem-solving and design across various disciplines. In mathematics, recognizing symmetrical patterns can simplify complex equations and reveal elegant solutions. In engineering, symmetrical designs often lead to more efficient and stable structures. Even in fields like computer science, symmetry concepts are applied in algorithms and data structures to optimize performance.
The Aesthetic Appeal and Psychological Effects of Symmetry
The human brain is naturally drawn to symmetry, perceiving it as a sign of order, balance, and beauty. This innate appreciation for symmetrical forms has deep evolutionary roots, possibly stemming from the recognition of healthy and genetically fit mates. In psychology, studies have shown that people tend to find symmetrical faces more attractive, highlighting the subconscious impact of symmetry on our perceptions.
The aesthetic appeal of symmetry extends beyond visual arts and into music, dance, and literature. In music, symmetrical structures in composition can create a sense of harmony and resolution. In dance, symmetrical movements often convey grace and coordination. Literature employs symmetry in narrative structures and poetic forms to create satisfying and memorable works.
The psychological effects of symmetry are profound and multifaceted. Symmetrical environments can induce feelings of calm and order, reducing stress and promoting well-being. In retail and marketing, symmetrical displays and packaging designs can increase product appeal and influence consumer behavior. The power of symmetry in branding is evident in the carefully crafted logos and visual identities of successful companies worldwide.
While perfect symmetry can be visually striking, it's worth noting that slight asymmetry or controlled imperfection can add interest and dynamism to designs. This concept, known as "dynamic symmetry," is often employed in photography and graphic design to create more engaging compositions that still maintain a sense of balance.
In conclusion, symmetry is a universal principle that transcends disciplines, influencing our perception of beauty, order, and functionality. From the intricate patterns of snowflakes to the grand designs of architectural marvels, symmetry continues to inspire and inform our understanding of the world. By recognizing and applying symmetry in various fields, we can unlock new possibilities in design, problem-solving, and scientific discovery, while also appreciating the aesthetic and psychological benefits it brings to our daily lives.
Conclusion
In this lesson, we explored the fascinating world of symmetry. We learned that symmetry is the property of an object remaining unchanged after certain transformations. Key methods for checking symmetry include reflection, rotation, and translation. We discovered symmetry's applications in art, architecture, and nature. The introduction video provided a crucial visual understanding of these concepts, making them more tangible. Symmetry is not just a mathematical concept but a fundamental principle in our world. We encourage you to practice identifying symmetry in your surroundings, from buildings to butterflies. This awareness will enhance your appreciation of the world's inherent order and beauty. As you become more comfortable with basic symmetry concepts, consider exploring more advanced topics like group theory and crystallography. Remember, symmetry is a gateway to understanding complex patterns in mathematics and science, offering endless opportunities for discovery and application in various fields.
Introduction to Basics of Symmetry
What is symmetry? What is a symmetrical shape?
Step 1: Understanding Symmetry
Symmetry is a fundamental concept in geometry and nature. When a shape has symmetry, it means that it can be divided into two identical parts that are mirror images of each other. These identical parts are called symmetrical parts, and the shape itself is referred to as a symmetrical shape. Symmetry is often observed in various objects around us, from simple geometric shapes to complex natural forms.
Step 2: Identifying Symmetrical Shapes
Symmetrical shapes are special because they consist of two exact same parts that face each other. This mirror effect is what defines the symmetry of the shape. For example, consider a heart shape or a chevron (arrowhead) shape. If you split these shapes down the middle, either vertically or horizontally, you will find that the two halves are identical and mirror each other.
Step 3: Examples of Symmetrical Shapes
Let's look at two examples to better understand symmetrical shapes. First, take a heart shape. If you split it vertically down the middle, the left side and the right side are exactly the same, just facing each other. Similarly, for a chevron shape, if you split it horizontally through the middle, the top part and the bottom part are identical and face each other.
Step 4: Verifying Symmetry
To verify if a shape is symmetrical, you can use a simple folding method. For instance, if you have a heart shape on a piece of paper, fold it along the middle line. If both sides align perfectly, then the shape is symmetrical. The same method can be applied to the chevron shape by folding it horizontally. If the top and bottom parts match up exactly, the shape is symmetrical.
Step 5: Line of Symmetry
The line that divides a symmetrical shape into two equal parts is called the line of symmetry. This line ensures that the two parts are congruent, meaning they are identical in shape and size. For example, in the heart shape, the vertical line down the middle is the line of symmetry. In the chevron shape, the horizontal line through the middle serves as the line of symmetry.
Step 6: Symmetrical vs. Asymmetrical Shapes
Not all shapes are symmetrical. To illustrate this, consider the outlines of two different trees. If you split one tree vertically and the two halves match up perfectly when folded, then the tree is symmetrical. However, if the halves do not align, the tree is asymmetrical. Asymmetrical shapes do not have a line of symmetry, meaning they cannot be divided into two identical parts.
Step 7: Conclusion
In conclusion, symmetry is a key concept in understanding shapes and their properties. Symmetrical shapes have a line of symmetry that divides them into two identical parts facing each other. This concept is not only important in geometry but also in various fields such as art, architecture, and nature. Recognizing and understanding symmetry helps us appreciate the balance and harmony in the world around us.
FAQs
-
What is symmetry in mathematics?
Symmetry in mathematics refers to the property of an object or shape remaining unchanged after certain transformations. These transformations can include reflection, rotation, or translation. For example, a square has four lines of symmetry and remains unchanged when rotated 90 degrees.
-
How can I check if a shape is symmetrical?
There are two main methods to check for symmetry: the folding method and the mirror test method. In the folding method, you fold the shape along a suspected line of symmetry and check if the halves align perfectly. The mirror test involves placing a mirror perpendicular to the surface along the suspected line of symmetry and checking if the reflection completes the shape seamlessly.
-
What is the relationship between the number of sides and lines of symmetry in regular polygons?
In regular polygons, the number of lines of symmetry is equal to the number of sides. For example, an equilateral triangle (3 sides) has 3 lines of symmetry, a square (4 sides) has 4 lines of symmetry, and so on. This relationship holds true for all regular polygons, making it a key characteristic of these shapes.
-
How is symmetry applied in the real world?
Symmetry has numerous real-world applications. In art and architecture, it's used to create visually pleasing and balanced designs. In nature, symmetry is found in various forms, from the bilateral symmetry of butterflies to the radial symmetry of flowers. In science, symmetry principles underpin many theories in physics and chemistry. Even in everyday objects, symmetry often plays a role in design for both aesthetic and functional purposes.
-
Can you give examples of symmetry in letters and numbers?
Many letters and numbers exhibit symmetry. For example, the letter 'A' has vertical symmetry, while 'B' has horizontal symmetry. Numbers like '0', '3', and '8' have both horizontal and vertical symmetry. Some words, when written in certain fonts, can also display symmetry. For instance, 'MATH' can exhibit vertical symmetry in some stylized fonts. Understanding symmetry in typography can be useful in design and logo creation.
Prerequisite Topics
Understanding the basics of symmetry is crucial in geometry, but to fully grasp this concept, it's essential to have a solid foundation in its prerequisite topics. Two key areas that form the building blocks of symmetry are line symmetry and rotational symmetry and transformations. These fundamental concepts are integral to developing a comprehensive understanding of symmetry in various geometric shapes and figures.
Line symmetry, also known as reflection symmetry, is a cornerstone of symmetry basics. It involves understanding how a shape can be divided into two identical halves by a line, called the line of symmetry. This concept is crucial because it helps students recognize patterns and balance in geometric figures, which is essential when studying more complex symmetrical structures. By mastering line symmetry, students can easily identify symmetrical objects in real life and apply this knowledge to solve more advanced geometric problems.
Equally important is the concept of rotational symmetry and transformations. This topic explores how shapes can be rotated around a central point while maintaining their original appearance. Understanding rotational symmetry is vital for grasping the basics of symmetry as it introduces the idea of symmetry in motion. It helps students visualize how objects can have multiple lines of symmetry and how symmetry can exist in three-dimensional space.
The relationship between these prerequisite topics and the basics of symmetry is profound. Line symmetry lays the groundwork for understanding reflections and mirror images, which are fundamental to many symmetrical patterns. Rotational symmetry, on the other hand, expands this understanding to include movement and transformation, showcasing how symmetry can be dynamic rather than static.
By studying line symmetry, students develop the ability to identify axes of symmetry in various shapes, from simple triangles to complex polygons. This skill is invaluable when analyzing more intricate symmetrical designs or when creating symmetrical patterns themselves. Similarly, a strong grasp of rotational symmetry and transformations allows students to understand concepts like order of rotational symmetry and how shapes can be manipulated while preserving their symmetrical properties.
These prerequisite topics not only provide the necessary tools for understanding the basics of symmetry but also foster critical thinking and spatial reasoning skills. They encourage students to look at geometric shapes from different perspectives, enhancing their overall geometric intuition. As students progress in their study of symmetry, they'll find that the principles learned from line and rotational symmetry continually resurface, reinforcing their importance in the broader context of geometry.
In conclusion, mastering the concepts of line symmetry and rotational symmetry and transformations is not just beneficial but essential for a comprehensive understanding of the basics of symmetry. These foundational topics provide the necessary framework for exploring more advanced symmetrical concepts and applications in geometry and beyond.

