Metric units: length, volume, weight
Topic Notes
In this lesson, we will learn:
- Metric units of length, volume and weigh
- Comparing and Converting between different metric units
- Choosing appropriate units to make measurements
Notes:
Metric Units of Length:
1km = 1000 m
1 m = 100 cm
1 cm = 10 mm
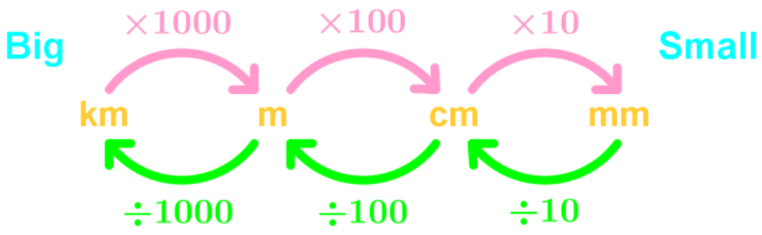
Metric Units of Volume
1L = 1000 mL
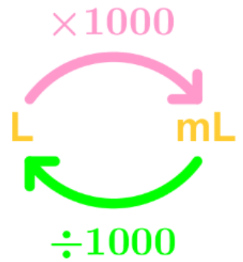
Metric Units of Weight
1kg = 1000 g
Introduction to Metric Units: Length, Volume, Weight
Welcome to our exploration of metric units! In this section, we'll dive into the fundamental concepts of length, volume, and weight in the metric system. These units form the backbone of scientific measurements and are essential for everyday life in many parts of the world. Our introduction video serves as a perfect starting point, offering a visual and engaging way to grasp these important concepts. As you watch, you'll discover how metric units provide a standardized system for measuring various aspects of our physical world. From the tiny millimeter to the vast kilometer, from the minuscule milliliter to the substantial liter, and from the light gram to the hefty kilogram, metric units offer a logical and interconnected approach to quantifying our surroundings. Understanding these units is crucial for students advancing in science, mathematics, and practical applications. So, let's embark on this journey to master metric measurements together!
Understanding Length in Metric Units
Length is a fundamental measurement that we encounter in our daily lives, from the size of a paperclip to the distance between cities. In the metric system, which is used by most countries worldwide, length is measured using various units, with the most common being millimeters (mm), centimeters (cm), meters (m), and kilometers (km). Let's explore these units and how they relate to one another.
Millimeters (mm)
The millimeter is the smallest commonly used metric unit of length. It's about the thickness of a credit card or the width of a grain of rice. Millimeters are perfect for measuring very small objects or precise dimensions in fields like engineering and manufacturing.
Centimeters (cm)
A centimeter is equal to 10 millimeters. This unit is often used to measure everyday objects. For example, a typical smartphone is about 15 cm long, and a pencil is roughly 20 cm in length. Centimeters are also commonly used in sewing and crafting.
Meters (m)
The meter is the base unit of length in the metric system. One meter is equal to 100 centimeters or 1,000 millimeters. Meters are used to measure larger objects and distances. For instance, the height of a door is typically about 2 meters, and a basketball hoop is set at 3.05 meters above the ground.
Kilometers (km)
For even greater distances, we use kilometers. One kilometer is equal to 1,000 meters. This unit is used for measuring long distances, such as the length of a road or the distance between cities. For example, a typical marathon race is 42.2 kilometers long.
Relationships Between Units
Understanding how these units relate to each other is crucial for effective measurement and conversion. Here's a quick breakdown:
- 1 cm = 10 mm
- 1 m = 100 cm = 1,000 mm
- 1 km = 1,000 m = 100,000 cm = 1,000,000 mm
Converting Between Length Units
Converting between metric units of length is straightforward due to the base-10 nature of the metric system. Here are some tips for conversion:
- To convert from a larger unit to a smaller unit, multiply by the appropriate power of 10. For example, to convert meters to centimeters, multiply by 100.
- To convert from a smaller unit to a larger unit, divide by the appropriate power of 10. For instance, to convert millimeters to meters, divide by 1,000.
Let's practice with some examples:
- Converting 5 meters to centimeters: 5 m × 100 = 500 cm
- Converting 2,500 millimeters to meters: 2,500 mm ÷ 1,000 = 2.5 m
- Converting 3.5 kilometers to meters: 3.5 km × 1,000 = 3,500 m
Remember, when working with metric units, you're often just moving the decimal point left or right. For example, 1.5 m is the same as 150 cm or 1,500 mm.
Real-World Applications
Understanding metric units of length is essential in many areas of life:
- In sports, track events are measured in meters, while long-distance races often use kilometers.
- In construction and interior design, room dimensions are typically given in meters or centimeters.
- In the medical field, body measurements might use centime
Exploring Weight in Metric Units
Weight is a fundamental concept in our daily lives, and understanding how to measure it accurately is essential. In the metric system, we primarily use two units to measure weight: grams (g) and kilograms (kg). Let's dive into these units and explore how they relate to each other.
Grams: The Building Blocks of Weight
The gram is the smallest commonly used unit of weight in everyday life. It's perfect for measuring lightweight items. For instance, a paperclip weighs about 1 gram, while a teaspoon of sugar is around 4 grams. Grams are ideal for measuring ingredients in cooking, especially when precision is key. A chocolate chip cookie recipe might call for 50 grams of butter or 100 grams of flour.
Kilograms: For Heavier Measurements
When we need to measure heavier objects, we turn to kilograms. One kilogram is equal to 1,000 grams. This unit is commonly used for measuring body weight, groceries, or luggage. An average adult might weigh around 70 kilograms, while a bag of potatoes at the supermarket could be 5 kilograms.
The Relationship Between Grams and Kilograms
Understanding the relationship between grams and kilograms is crucial for accurate measurements. Here's a simple breakdown:
- 1 kilogram = 1,000 grams
- 0.5 kilograms = 500 grams
- 0.1 kilograms = 100 grams
This relationship makes it easy to convert between the two units, which is often necessary in cooking, science experiments, or when following product instructions.
Converting Between Grams and Kilograms
Converting between grams and kilograms is straightforward once you understand their relationship. Here's how to do it:
From Grams to Kilograms:
To convert grams to kilograms, divide the number of grams by 1,000. For example:
- 2,500 grams = 2,500 ÷ 1,000 = 2.5 kilograms
- 750 grams = 750 ÷ 1,000 = 0.75 kilograms
From Kilograms to Grams:
To convert kilograms to grams, multiply the number of kilograms by 1,000. For instance:
- 3.5 kilograms = 3.5 × 1,000 = 3,500 grams
- 0.25 kilograms = 0.25 × 1,000 = 250 grams
Practical Examples in Everyday Life
Let's look at some real-life scenarios where understanding weight measurements is useful:
- Cooking: A recipe calls for 250 grams of flour. If your scale only shows kilograms, you'd know this is 0.25 kilograms.
- Shipping: If you're mailing a package and the weight limit is 2 kilograms, you know it can't exceed 2,000 grams.
- Fitness: If you're tracking your weight loss and you've lost 500 grams, that's equivalent to 0.5 kilograms.
- Shopping: When buying fruits, you might see prices per kilogram, but you're only buying 200 grams of berries.
Why Understanding Weight
Understanding weight in the metric system is essential for various practical applications in daily life, from cooking to shopping and fitness tracking.
Discovering Volume in Metric Units
Welcome to the fascinating world of volume measurement! Today, we're going to explore the concept of volume and its metric units, focusing on milliliters and liters. These units are essential for measuring liquid capacity, and understanding them will help you in various aspects of daily life, from cooking to science experiments.
What is Volume?
Volume is the amount of space that a substance or object occupies in three dimensions. When it comes to liquids, we often refer to this as capacity. Imagine filling up a container with water the amount of water it can hold is its volume or capacity.
Introducing Milliliters and Liters
In the metric system, we primarily use two units to measure liquid volume: milliliters (mL) and liters (L). Let's break them down:
- Milliliter (mL): This is a very small unit of volume. Think of a drop of water it's about 0.05 mL. A teaspoon is about 5 mL.
- Liter (L): This is a larger unit of volume. One liter is equal to 1000 milliliters. A typical water bottle often contains 500 mL or 0.5 L.
Using Milliliters and Liters in Everyday Life
You'll encounter these units in many situations:
- Cooking recipes often list ingredients in mL or L (e.g., 250 mL of milk)
- Soft drinks are commonly sold in 330 mL cans or 2 L bottles
- Medicine dosages are usually given in mL
- Fuel for your car is measured in liters
The Relationship Between Milliliters and Liters
Understanding the relationship between these units is crucial. Here's the key conversion to remember:
1 Liter = 1000 Milliliters
This means that:
- 0.5 L = 500 mL
- 0.1 L = 100 mL
- 1.5 L = 1500 mL
Converting Between Milliliters and Liters
Converting between these units is straightforward once you understand their relationship. Let's look at some examples:
Converting from Liters to Milliliters
To convert liters to milliliters, multiply by 1000.
Example: Convert 2.5 L to mL
2.5 L × 1000 = 2500 mL
Converting from Milliliters to Liters
To convert milliliters to liters, divide by 1000.
Example: Convert 3500 mL to L
3500 mL ÷ 1000 = 3.5 L
Practical Examples
Let's apply this knowledge to some real-life scenarios:
- If a recipe calls for 750 mL of water, you could also say it needs 0.75 L.
- A large soda bottle containing 2 L is the same as 2000 mL.
- If you need to take 5 mL of medicine twice a day for a week, you'll use 70 mL in total (
Practical Applications of Metric Units
Metric units are an integral part of our daily lives, playing a crucial role in various fields and activities. From the laboratory to the kitchen, and from construction sites to international trade, these standardized measurements help us communicate and work with precision. Let's explore some real-world applications of metric units and understand their importance in a global context.
In the realm of science, metric units are the backbone of accurate measurements and calculations. Scientists use milliliters to measure small volumes of liquids in experiments, while kilometers help astronomers describe vast cosmic distances. The video we watched earlier showed how easy it is to convert between metric units, which is essential in scientific calculations. For instance, a biologist might measure the length of a cell in micrometers and then need to convert it to millimeters for a report.
Cooking is another area where metric units shine. Many recipes, especially those from countries outside the United States, use grams for dry ingredients and milliliters for liquids. This precision ensures consistent results every time you cook. Remember how we learned about the relationship between grams and milliliters for water? This knowledge comes in handy when following recipes. For example, if a recipe calls for 250 ml of water, you know it's the same as 250 grams, making it easy to measure with either a liquid measuring cup or a kitchen scale.
In the construction industry, metric units are widely used for their ease of calculation and precision. Architects and engineers often work in meters and centimeters when designing buildings. The simplicity of converting between these units, as demonstrated in the video, helps in scaling plans and ensuring accurate measurements on-site. For instance, if a room is 4.5 meters long, a builder can quickly calculate that it's 450 centimeters without complex math.
Understanding metric units becomes even more critical in our increasingly interconnected world. Most countries use the metric system, making it essential for international communication and trade. When you travel abroad, you'll encounter temperatures in Celsius, distances in kilometers, and fuel efficiency measured in liters per 100 kilometers. Being familiar with these units helps you navigate foreign environments more easily.
In the realm of sports, metric units are standard in many international competitions. Runners compete in 100-meter sprints and 42.2-kilometer marathons. Swimmers race in 50-meter pools. Even in countries that primarily use imperial units, like the United States, you'll find track and field events measured in meters.
Healthcare is another field where metric units are crucial. Medications are dosed in milligrams or milliliters, and patient weights are often recorded in kilograms. This standardization helps prevent errors and ensures consistent care across different healthcare systems worldwide.
In everyday life, you might encounter metric units more often than you realize. Soft drinks come in 2-liter bottles, and many food products list nutritional information in grams. When you buy fabric, it's often sold by the meter. Even in countries that don't officially use the metric system, many products include metric measurements alongside imperial units.
Understanding metric units is not just about following recipes or reading road signs in foreign countries. It's about being part of a global community that shares a common language of measurement. As we saw in the video, the simplicity and logic of the metric system make it an invaluable tool for communication and collaboration across borders and disciplines.
In conclusion, the practical applications of metric units are vast and varied. From the precise measurements needed in scientific research to the everyday tasks of cooking and shopping, metric units provide a consistent and easy-to-use system of measurement. As our world becomes increasingly connected, the ability to understand and use metric units becomes not just useful, but essential. So the next time you measure ingredients for a recipe or check the temperature while traveling abroad, remember that you're participating in a global system of measurement that connects us all.
Common Conversions and Tricks for Remembering Metric Units
Mastering metric unit relationships and conversions can be a breeze with the right tips and tricks! Let's explore some helpful strategies to make learning and remembering these essential measurements a fun and easy process. One of the most effective ways to grasp metric units is through mnemonic devices and visual aids. These memory tools can transform complex information into easily digestible chunks that stick in your mind.
First, let's tackle the metric prefixes. Remember the phrase "King Henry Died By Drinking Chocolate Milk" to recall the order of prefixes from largest to smallest: Kilo-, Hecto-, Deca-, Base unit, Deci-, Centi-, Milli-. This mnemonic device helps you quickly navigate through different metric scales. For a visual aid, imagine a staircase where each step represents a power of 10, with the base unit in the middle. As you climb up, you're multiplying by 10, and as you descend, you're dividing by 10.
When it comes to common conversions, it's useful to have a few key relationships memorized. For instance, 1 kilometer is equal to 1000 meters, and 1 meter is 100 centimeters. A handy trick for length conversions is to remember that a meter is slightly longer than a yard about 1.1 yards. This can help you estimate distances when switching between metric and imperial units.
For volume, visualize that a liter is slightly larger than a quart. Specifically, 1 liter is about 1.06 quarts. This approximation can be incredibly useful when cooking or estimating liquid measurements. When dealing with mass, keep in mind that 1 kilogram is roughly 2.2 pounds. A fun way to remember this is to think of a 1-kg bag of sugar, which is noticeably heavier than a 2-pound bag.
Temperature conversions between Celsius and Fahrenheit can be tricky, but here's a simple trick: double the Celsius temperature and add 30 for a close Fahrenheit estimate. For example, 20°C doubled is 40, plus 30 gives you 70°F which is quite close to the actual 68°F. This method works well for everyday temperatures.
Visual aids can be incredibly powerful for learning metric conversions. Create a mental image of common objects for each unit. For example, a paperclip weighs about a gram, a textbook is close to a kilogram, and a small car weighs about a metric ton. These tangible references make abstract measurements more concrete and relatable.
Another helpful trick is to use your body as a measuring tool. The width of your pinky finger is approximately 1 centimeter, while your arm span is close to your height in meters. These built-in "rulers" can be handy for quick estimations when you don't have measuring tools available.
Remember, practice makes perfect! Try incorporating these conversions into your daily life. Estimate the length of your room in meters, guess the weight of your groceries in kilograms, or convert the day's temperature to Celsius. The more you engage with these units, the more natural they'll become.
Lastly, don't forget to leverage technology. Many smartphones have built-in conversion tools that can help you double-check your mental calculations. Use these resources to reinforce your learning and build confidence in your conversion skills. With these tips, tricks, and a positive attitude, you'll be a metric conversion pro in no time!
Conclusion: Mastering Metric Units
In this journey through metric units, we've explored the fundamental measures of length, volume, and weight. The metric system's consistency and ease of conversion make it a powerful tool for scientific and everyday use. Remember, meters, liters, and grams form the foundation, with prefixes modifying these base units. The introduction video provided a crucial visual understanding of these concepts, helping to solidify your grasp on metric measurements. As you continue your learning, practice is key to mastery. Challenge yourself to estimate measurements in your daily life using metric units. Explore real-world applications, from cooking to construction, where metric units shine. With each exercise, you'll build confidence and fluency in this universal language of measurement. Embrace the metric system's elegance and precision, and you'll find a world of possibilities opening up before you. Keep exploring, keep measuring, and keep growing in your metric mastery!
Introduction to Metric Units
Introduction to measuring length
- What is length?
- How do we measure length?
- Metric Units of Length: millimetre, centimetre, meter, kilometer
Step 1: Understanding Length
Length is a measure of how long something is. It is the distance from one end of an object to the other. For example, if you have a book and you want to know its length, you measure the distance from one end of the book to the other. This distance is what we refer to as the length of the book.
Step 2: Measuring Length
To measure length, you can use various tools. In the example provided, a phone was used as a measuring tool. If the book is measured to be two phones long, then the length of the book is two phones. Similarly, if an eraser is measured to be one phone long, then the length of the eraser is one phone. By comparing these measurements, you can determine which object is longer. However, using different tools (like different-sized phones) can lead to different measurements for the same object. This is why standardized units are important.
Step 3: Introduction to Metric Units of Length
To avoid confusion and ensure consistency in measurements, standardized units called metric units are used. These units are the same length for everyone, ensuring that measurements are consistent. The metric units of length include millimeters (mm), centimeters (cm), meters (m), and kilometers (km). These units allow for precise and consistent measurements across different objects and distances.
Step 4: Small and Large Units
Metric units come in different sizes to measure various lengths. For example, a millimeter (mm) is a very small unit, about the width of a credit card. A centimeter (cm) is slightly larger, about the width of an index finger. A meter (m) is much larger, roughly the width of a door or the length of a big step. A kilometer (km) is even larger, equivalent to a thousand big steps. These different units allow for measuring both small objects, like a pencil, and large distances, like the distance between two cities.
Step 5: Abbreviations for Metric Units
To make it easier to write and read measurements, metric units have standard abbreviations. Millimeters are abbreviated as mm, centimeters as cm, meters as m, and kilometers as km. These abbreviations help in quickly identifying the unit of measurement without writing out the full word.
Step 6: Practical Examples of Metric Units
Using practical examples can help understand the use of different metric units. For instance, measuring a pencil might be best done in centimeters or millimeters, while measuring the distance between two cities would be more practical in kilometers. This way, you can choose the appropriate unit based on the size of the object or distance being measured.
Step 7: Relationship Between Metric Units
Metric units are related to each other, allowing for easy conversion between them. For example, if you have a measurement in centimeters, you can convert it to millimeters by understanding their relationship. This relationship helps in converting measurements without having to re-measure the object. In the next steps, you can learn how to convert between different metric units to make measurements more versatile and practical.
Step 8: Conclusion
Understanding metric units and their use in measuring length is crucial for accurate and consistent measurements. By using standardized units like millimeters, centimeters, meters, and kilometers, you can ensure that your measurements are precise and comparable. This introduction provides a foundation for further learning about how these units are related and how to convert between them for various measurement needs.
FAQs
-
What are the basic units of length, volume, and weight in the metric system?
The basic units in the metric system are: - Length: meter (m) - Volume: liter (L) - Weight/Mass: gram (g) These base units can be modified with prefixes to represent larger or smaller measurements.
-
How do you convert between different metric units?
To convert between metric units, you typically multiply or divide by powers of 10. For example: - To convert from meters to centimeters, multiply by 100 (1 m = 100 cm) - To convert from kilograms to grams, multiply by 1000 (1 kg = 1000 g) - To convert from liters to milliliters, multiply by 1000 (1 L = 1000 mL) Moving to a smaller unit involves multiplication, while moving to a larger unit involves division.
-
What are some common prefixes used in the metric system?
Common metric prefixes include: - kilo- (k): 1000 times the base unit - centi- (c): 1/100 of the base unit - milli- (m): 1/1000 of the base unit - deci- (d): 1/10 of the base unit - hecto- (h): 100 times the base unit These prefixes can be applied to the base units to create a wide range of measurements.
-
How does the metric system compare to the imperial system?
The metric system is based on units of 10, making conversions simpler. It's used globally in science and most countries. The imperial system, used primarily in the US, has more complex conversion factors. For example: - 1 inch = 2.54 centimeters - 1 pound 454 grams - 1 gallon 3.78 liters The metric system's consistency makes it easier for international communication and scientific work.
-
What are some practical applications of metric units in everyday life?
Metric units are used in various everyday situations: - Cooking: recipes often use grams and milliliters - Sports: running distances in meters or kilometers - Medicine: drug dosages in milligrams or milliliters - Weather: temperature in Celsius, rainfall in millimeters - Retail: food sold by kilograms, fabric by meters Understanding metric units helps in cooking, traveling to countries using the metric system, and interpreting product information.
Prerequisite Topics
Understanding metric units for length, volume, and weight is crucial in various fields, from science to everyday life. To fully grasp this topic, it's essential to have a solid foundation in several prerequisite concepts. These foundational topics not only enhance your understanding but also provide context for the practical applications of metric units.
One key prerequisite is conversions involving squares and cubic measurements. This knowledge is vital when dealing with area and volume calculations in the metric system. For instance, when converting square meters to square centimeters or cubic liters to milliliters, understanding these conversions becomes indispensable. This skill allows for seamless transitions between different metric units and their squared or cubed forms, which is particularly useful in fields like engineering and architecture.
Another important prerequisite is determining the number of solutions to linear equations. While this may seem unrelated at first glance, it actually plays a significant role in understanding the base-10 number system, which is the foundation of metric units. The metric system's simplicity and ease of use stem from its decimal nature, where each unit is ten times larger or smaller than the adjacent unit. This decimal relationship makes conversions within the metric system straightforward and logical.
Lastly, familiarity with conversions between metric and imperial systems is crucial. In our globally connected world, being able to switch between these two systems is invaluable. This skill is particularly useful when dealing with temperature conversions between Celsius and Fahrenheit, which often come up in scientific studies, weather reports, and international travel. Understanding these conversions helps bridge the gap between different measurement systems used worldwide.
By mastering these prerequisite topics, students gain a comprehensive understanding of the metric system's structure and applications. The knowledge of square and cubic conversions allows for accurate area and volume calculations. Understanding linear equations and the base-10 system provides insight into the logical progression of metric units. Finally, the ability to convert between metric and imperial systems ensures practical application in various real-world scenarios.
In conclusion, these prerequisite topics form the backbone of understanding metric units for length, volume, and weight. They provide the necessary context and skills to navigate the metric system confidently, making it easier to apply this knowledge in both academic and practical settings. As students progress in their studies of metric units, they'll find that these foundational concepts continually resurface, reinforcing their importance in mastering the subject.

