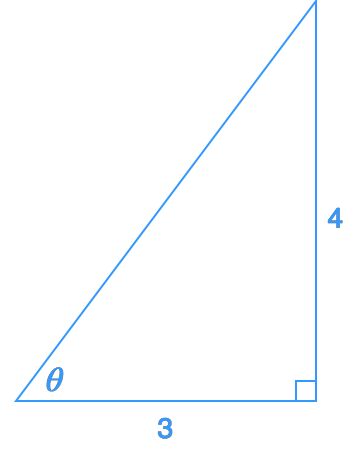
Derivative of Arctan
There are many students that find it easy to take derivatives of trig functions, but many struggle with derivatives of inverse trig functions. We will first talk about the many types of inverse trig functions we can differentiate, and then talk in detail about the first and second derivative of arctan.
Derivatives of inverse Trig Functions
First of all, there are exactly a total of 6 inverse trig functions. They are arcsin x, arccos x, arctan x, arcsec x, and arccsc x. However, some teachers use the power of -1 instead of arc to express them. For example, arcsin x is the same as . The derivative of each trig function is written below.
-
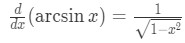
Formula 1: Derivative of arcsinx -
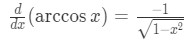
Formula 2: Derivative of arccosx -
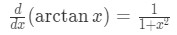
Formula 3: Derivative of arctanx -
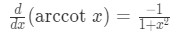
Formula 4: Derivative of arccotx -
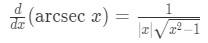
Formula 5: Derivative of arcsecx -
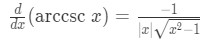
Formula 6: Derivative of arccscx
Notice that the derivative of arctan x and arccot x are very similar. In fact, they only differ by a negative sign so make sure you remember it correctly!
Derivative of arctan formula
Now a lot people can memorize these formulas, but not many people actually understand how we get them. For example, the derivative of arctan x is:
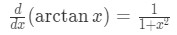
How is that even possible? Well first of all we want to start from the beginning. Let's take a look at:
-
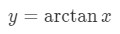
Equation 1: Derivative of arctan pt.1 Notice that is the same as .Now let us move the inverse tangent to the left side of the equation. Doing this will give us:
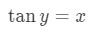
Equation 2: Derivative of arctan pt.2 Now what we want to do here is something called implicit differentiation. In other words, we want to take the derivative of both sides of the equation. Doing so will give us,
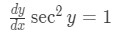
Equation 3: Derivative of arctan pt.3 Notice that shows up in the equation because of the chain rule. If you don't understand chain rule or trig derivatives that well, then click those links!
Now dividing both sides of the equation by will give us:
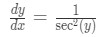
Equation 4: Derivative of arctan pt.4 We are really close! Next, we look at the trig identity
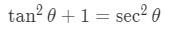
Formula 7: Trig identity 1 Notice that we can substitute this identity into our equation, which will give us:
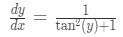
Equation 5: Derivative of arctan pt.5 Notice that this question requires you to know Pythagorean identities . So make sure you know them well before continuing with the question.
Now going back on topic, recall that , so . Substituting this into the equation will finally give us the following formula:
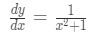
Equation 6: Derivative of arctan pt.6
If you are still having trouble understanding, I recommend you look at the intro video or look at this link, http://oregonstate.edu/instruct/mth251/cq/Stage6/Lesson/invTrigDeriv.html
Second derivative of arctan
First of all recall that the first derivative of arctan is:
-
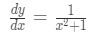
Equation 6: Derivative of arctan pt.6 Taking the second derivative is not that challenging because we only need to use the quotient rule. Recall that the formula of the quotient rule is:
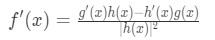
Formula 8: Quotient Rule The second derivative will be:
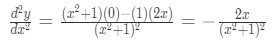
Equation 7: Second Derivative of arctan pt.1 Hence we can conclude that:
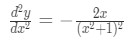
Equation 8: Second Derivative of arctan pt.2
Derivative of Other Inverse Trig Functions (arcsec)
What we start to notice after differentiating each inverse trig function is that they all have the same general idea. For example when taking the derivative of arctan, we moved the inverse tangent to the other side, did implicit differentiation, and used the trig identity. You will find that you can do the exact same thing for differentiating arccos x, arcsin x, and arccot x. The only difference is that the trig identity you use may be different. For example, arccos x and arcsin x uses the trig identity
-
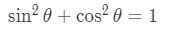
Formula 9: Trig Identity 2 However, the derivative of arcsec and arccsc is slightly more different. For example, let us try to take the derivative of arcsec. We start with the equation,
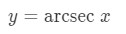
Equation 9: Derivative of arcsec pt.1 Notice that y = arcsec x is the same as . Now moving the inverse tangent to the other side of the equation will give us
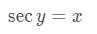
Equation 10: Derivative of arcsec pt.2 Using implicit differentiation again will give us the equation:
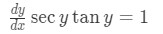
Equation 11: Derivative of arcsec pt.3 Note that the derivative of is and the chain rule gives us . Now dividing both sides of the equation by gives us:
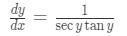
Equation 12: Derivative of arcsec pt.4 Here is where it gets a little different.
Remember that we have the trig identity
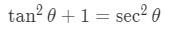
Formula 7: Trig identity 1 Now let us isolate tan in this trig identity. Doing a little bit of algebraic manipulation will give us that
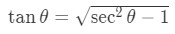
Equation 13: Derivative of arcsec pt.5 Now if we change all our 's to y's and substitute tan y in our derivative equation, then we will get that
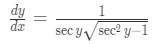
Equation 14: Derivative of arcsec pt.6 Lastly, we know that , hence substituting that will lead us to our equation:
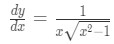
Equation 15: Derivative of arcsec pt.7 You may notice that our x in the equation is missing an absolute value. Why is that? It is because x can actually never be negative. If you want to know more about that in detail, please look at the last theorem in this link.
Hence we need to include the absolute value manually, which means that
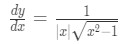
Equation 16: Derivative of arcsec pt.8
Here are formulas to deriving inverse trigonometric functions
arcsin
arccos
arctan
arccot
arcsec
arccsc