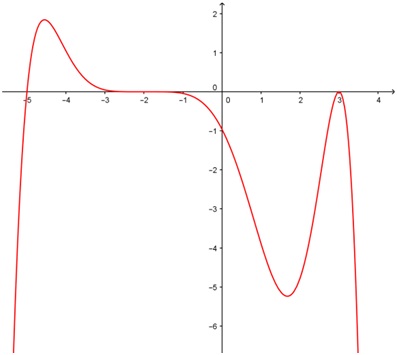
The multiplicity of a zero corresponds to the number of times a factor is repeated in the function.
Odd multiplicity: cross the x-axis
Odd multiplicity (3 or more): changes concavity when passing through x-axis
Even multiplicity: bounces off the x-axis
Odd multiplicity: cross the x-axis
Odd multiplicity (3 or more): changes concavity when passing through x-axis
Even multiplicity: bounces off the x-axis