Patterns with shapes
Topic Notes
In this lesson, we will learn:
- How to identify patterns with shapes
- How to describe and draw sequences of figures (compound shapes)
- How to predict the next figure in a sequence with shapes and numbers
Notes:
- A pattern is something that repeats over and over again
- It could be a set of number, alphabetic letters, colors, objects, shapes, etc.
- To create a pattern with shapes, there must be a repeated order
- Ex. triangle, triangle, square, triangle, triangle, square, triangle …

- The order of shapes goes “triangle, triangle, square” and repeats
- Using the pattern, you can predict what shape will come next (for this example, the next shape in the pattern is a triangle)
- More complicated shape patterns use multiple shapes to build compound shapes
- Each new form of the shape can be called a figure in the pattern sequence
- A sentence description can be used to describe a pattern and help predict the next figure
- Ex. “add one more block to the right and bottom sides of the figure each time”
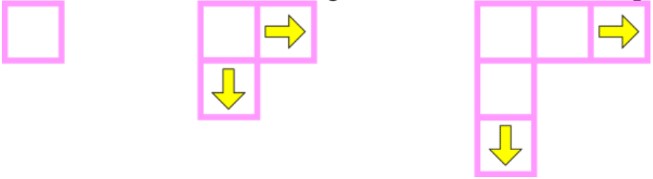
- Creating a table for the figure number and the number of shapes can help you see number patterns too!

- For this pattern, two more squares are added each time. You can predict that the 4th figure will have 7 squares (5+2=7)
Introduction to Patterns with Shapes
Welcome to our exploration of patterns with shapes! As we begin this exciting journey, let's start by watching the introduction video. This video is crucial in laying the foundation for understanding visual patterns and how they work with different shapes. Patterns are all about repetition and recognizing sequences, which is a fundamental skill in mathematics. You'll see how simple shapes like circles, squares, and triangles can create fascinating patterns when arranged in specific ways. These patterns aren't just visually appealing; they're also key to developing your problem-solving skills and spatial awareness. As we progress, you'll learn to identify, continue, and even create your own patterns using various shapes. Remember, patterns are everywhere in our world, from nature to architecture, and understanding them will help you see the world in a whole new way. Let's dive in and discover the wonderful world of patterns together!
Understanding Basic Patterns with Shapes
Patterns are all around us, and understanding them is an important skill for young learners. Let's explore the exciting world of basic patterns using shapes! A pattern is a sequence of objects, shapes, or numbers that repeats in a predictable way. When we talk about patterns with shapes, we're looking at how different geometric shapes like squares, triangles, and circles can be arranged in a repeating order.
Imagine you have a row of shapes that goes: square, circle, triangle, square, circle, triangle. This is a simple pattern! The sequence "square, circle, triangle" keeps repeating, creating a pattern that's easy to recognize and continue. Let's look at some more examples of patterns using different shapes:
- Circle, square, circle, square, circle, square
- Triangle, triangle, square, triangle, triangle, square
- Square, circle, circle, square, circle, circle
Can you see how each of these patterns has a repeating segment? That's the key to understanding patterns - identifying the part that keeps repeating. Once you spot the repeating part, you can predict what comes next in the pattern.
Here's a fun way to visualize a pattern:
In this pattern, we have a red circle, an orange diamond, and a blue circle repeating. Can you guess what shape would come next?
Patterns can also be more complex. They might use different colors along with shapes, or they might have a longer sequence before it repeats. For example:
Here, we have a pattern of colored circles alternating with white circles. The repeating segment is "red circle, white circle, blue circle, white circle".
To identify repeating segments in patterns, follow these steps:
- Look at the beginning of the pattern.
- Try to find where the sequence starts to repeat.
- Check if this sequence continues throughout the pattern.
- If it does, you've found the repeating segment!
Patterns are not just fun to create and identify; they're also important in math and science. They help us make predictions and understand sequences in the world around us. For instance, the changing seasons follow a pattern, and so do the days of the week!
Here's a slightly more challenging pattern to try:
Can you identify the repeating segment in this pattern? It's "two triangles and a red circle, followed by two diamonds and a blue circle".
Remember, patterns can be found everywhere - in nature, in art, in music, and even in our daily routines. By learning to recognize and create patterns with shapes, you're developing important skills that will help you in many areas of life and learning.
Practice making your own patterns with shapes. You can draw them, use stickers, or even arrange objects around your home. Try creating patterns with two shapes, then three, and see if you can make more complex patterns as you get better at it. Don't forget to explain your patterns to friends or family - teaching others is a great way to reinforce your own understanding!
As you explore the world of patterns, keep these key ideas in mind:
- Patterns have a repeating sequence
- They can use different shapes, colors, or both
- Identifying the
Creating Patterns with Multiple Shapes
Creating complex patterns using multiple shapes is an exciting way to explore geometry and develop pattern recognition skills. This process involves understanding the concept of a repeated motif and how it can incorporate several different shapes to form intricate and visually appealing sequences. By mastering these techniques, you'll be able to create, recognize, and predict more sophisticated patterns.
A repeated motif is a fundamental element in pattern creation. It's a sequence of shapes that repeats throughout the pattern, forming its core structure. While simple patterns might use just one shape, more complex patterns incorporate multiple shapes within a single motif. This combination of shapes adds depth and interest to the overall design.
Let's explore some examples of patterns with multiple shapes:
1. Two-shape pattern: Consider a pattern that alternates between a circle and a square. The motif here would be "circle, square," and it would repeat continuously. This simple yet effective pattern could be represented as:
2. Three-shape pattern: A more complex pattern might use a triangle, a star, and a hexagon. The repeated motif could be "triangle, star, hexagon," creating a sequence like this:
3. Four-shape pattern: For an even more intricate design, we could use a circle, square, triangle, and diamond. The motif "circle, square, triangle, diamond" would create a pattern like this:
When working with multiple shapes, it's essential to consider not only the shapes themselves but also their sizes, colors, and orientations. These factors can add additional layers of complexity to your patterns. For instance, you might create a pattern where shapes gradually increase in size or rotate slightly with each repetition.
To truly understand and appreciate these patterns, it's crucial to practice predicting the next shape in a sequence. This skill helps develop pattern recognition and logical thinking. Here are some exercises to hone your prediction skills:
Exercise 1: Predict the next shape in this sequence: ?
In this pattern, we see a repeating motif of "circle, square, triangle." Therefore, the next shape would be a circle ().
Exercise 2: What comes next in this pattern: ?
Here, we have a more complex motif: "star, hexagon, triangle, star, hexagon, square." The pattern then repeats, so the next shape would be a star ().
Exercise 3: Determine the next two shapes in this sequence: ?
In this pattern, the motif is "circle, diamond, square, triangle." Therefore, the next two shapes would be a diamond () followed by a square ().
As you work with multiple shapes and more complex patterns, consider these tips:
1. Start by identifying the individual shapes used in the pattern.
2. Look for repeating sequences or motifs within the larger pattern.
3. Pay attention to any variations in size, color, or orientation of the shapes.
4. Practice creating your own patterns using different combinations of shapes.
5. Challenge yourself to recognize and predict patterns quickly.
Creating patterns with multiple shapes not only enhances your understanding of geometry but also develops critical thinking and creativity. As you become more proficient, you'll find that these skills have applications in various fields, from art and design to mathematics and computer science.
Remember, the key to mastering pattern creation and recognition is practice. Start with simple two-shape patterns and gradually increase complexity as you become more comfortable. Experiment with different shapes, sizes, and arrangements to create unique and visually striking patterns. By doing so, you'll develop a keen eye for design and a deeper appreciation for the mathematical principles underlying pattern sequences.
In conclusion, working
Analyzing Patterns with Numbers and Tables
Analyzing patterns with shapes using numbers and tables is a fundamental skill in numerical analysis and pattern recognition. This process involves carefully examining a sequence of figures, counting the shapes within each, and organizing data to identify trends and make predictions. Let's explore this concept step-by-step.
To begin, let's consider a simple pattern sequence with geometric shapes. Imagine a series of figures where each subsequent figure adds more shapes in a predictable manner. The first step in analyzing this pattern is to count the number of shapes in each figure accurately. This process requires attention to detail and systematic counting techniques.
For example, let's say we have a sequence where Figure 1 has 2 circles, Figure 2 has 4 circles, and Figure 3 has 6 circles. By counting and recording these numbers, we start to see a numerical pattern emerging. This is where creating tables for patterns become incredibly useful in organizing data and visualizing the data.
Creating a table to represent this information might look like this:
Figure Number Number of Circles 1 2 2 4 3 6 With this table, we can more easily identify the numerical pattern. In this case, we see that the number of circles increases by 2 with each figure. This observation is crucial for making predictions about future figures in the sequence.
To further analyze the pattern, we might add another column to our table to show the difference between consecutive figures:
Figure Number Number of Circles Difference 1 2 - 2 4 +2 3 6 +2 This expanded table clearly shows the consistent increase of 2 circles per figure. Using this information, we can now predict the number of circles in future figures. For Figure 4, we would expect 8 circles, for Figure 5, 10 circles, and so on.
The power of using tables in pattern analysis extends beyond simple arithmetic sequences. More complex patterns might involve multiple shapes or varying rates of change. In such cases, creating tables for patterns with separate columns for each type of shape can help identify individual patterns within the larger sequence.
For instance, consider a pattern where each figure contains both circles and squares, with the number of each shape changing differently:
Figure Number Circles Squares Total Shapes 1 1 2 3 2 3 3 6 3 5 4 9 In this more complex example, we can observe that the
Creating Compound Shapes in Patterns
Compound shapes in patterns are an intriguing concept that combines basic geometric forms to create more complex and visually appealing designs. These patterns are not only aesthetically pleasing but also serve as a foundation for understanding numerical sequences and spatial relationships. By exploring compound shapes, we can unlock a world of pattern recognition and mathematical analysis.
At its core, a compound shape is formed by combining two or more simple shapes to create a more intricate figure. This process of building upon a base shape is fundamental to creating pattern sequences. For example, starting with a simple square, we can add triangles to each side to form a star-like shape. This new compound shape can then become the basis for further additions and variations.
To create pattern sequences using compound shapes, we begin with a basic geometric form such as a circle, square, or triangle. This serves as our foundation or base shape. From there, we systematically add blocks or shapes according to a specific rule or pattern. For instance, we might start with a triangle and add a small square to each of its sides. In the next iteration, we could add triangles to the outer edges of these squares, creating a more complex snowflake-like pattern.
Let's consider some examples to illustrate this concept. Imagine starting with a simple pentagon. In the first step, we add a small triangle to each side of the pentagon. For the second step, we might add a square to each of the newly formed triangles. This process can continue, with each iteration adding new shapes or modifying existing ones according to a predetermined rule.
Another example could involve starting with a circle. We could add small semicircles around its circumference in the first step. In the next iteration, we might add smaller circles at the endpoints of each semicircle. This process of building upon the previous shape creates a fascinating fractal-like pattern that grows in complexity with each step.
Analyzing these patterns numerically is an essential aspect of understanding compound shapes in sequences. As we build upon our base shape, we can track various numerical properties. For instance, we might count the number of sides or vertices in each iteration of the pattern. This could lead to discovering interesting numerical sequences such as arithmetic and geometric progressions.
To analyze compound shape patterns numerically, we can focus on several aspects:
1. Count the number of each type of shape used in each iteration.
2. Measure the perimeter or area of the compound shape as it grows.
3. Calculate the ratio between different elements of the pattern.
4. Identify any recurring numerical patterns in the sequence of shapes.For example, if we start with a square and add triangles to each side in each iteration, we might observe that the number of triangles follows the sequence 4, 8, 16, 32, and so on doubling with each step. This geometric progression can be expressed mathematically as 4 * 2^(n-1), where n is the iteration number.
Similarly, we could analyze the total number of sides in our compound shape. Starting with a square (4 sides) and adding triangles, we'd see the sequence 4, 12, 28, 60, and so on. This sequence follows a more complex pattern that can be described by the formula 4(2^n - 1), where n is the iteration number.
Understanding these numerical relationships not only helps in predicting future iterations of the pattern but also provides insights into the underlying mathematical principles governing the growth of compound shapes.
Compound shapes in patterns offer a rich field for exploration, combining visual creativity with mathematical analysis. By starting with simple base shapes and systematically adding new elements, we can create intricate and beautiful designs. The process of building these patterns step by step allows us to observe and analyze the numerical relationships that emerge, fostering a deeper understanding of geometry, sequences, and mathematical modeling.
Whether used in art, design, or mathematical education, compound shapes in patterns serve as a powerful tool for developing spatial reasoning and pattern recognition skills. They demonstrate how simple rules can lead to complex and fascinating results, illustrating the beauty and order inherent in mathematical structures. By engaging with these patterns, we can enhance our ability to recognize and create sequences, a skill that has applications far beyond the realm of geometry, extending into fields such as computer science, data analysis, and even natural analyzing numerical relationships in patterns.
Advanced Pattern Recognition and Creation
As we delve deeper into the world of advanced patterns, we encounter more complex concepts that involve rotation, reflection, and scaling of shapes. These transformations add depth and sophistication to pattern recognition and creation, challenging our perception and analytical skills.
Rotational patterns are those that involve turning shapes or elements around a central point. A classic example is the spiral pattern found in sunflowers or nautilus shells. To create a rotational pattern, start with a basic shape and rotate it at regular intervals around a fixed point. The degree of rotation and the number of repetitions can vary, creating diverse and intricate designs.
Reflection, or mirror symmetry, is another crucial concept in advanced pattern recognition. This transformation involves creating an exact mirror image of a shape or pattern across an axis. Butterfly wings and certain types of flowers exhibit natural reflection patterns. To analyze reflective patterns, look for the line of symmetry and observe how elements are mirrored on either side.
Scaling patterns involve changing the size of shapes or elements while maintaining their proportions. Fractals are excellent examples of scaling patterns in nature, where similar shapes repeat at different scales. The Sierpinski triangle is a famous mathematical pattern that demonstrates scaling. To create scaling patterns, start with a base shape and replicate it at different sizes, often in a nested or recursive manner.
Advanced patterns often combine multiple transformations, creating complex and visually striking designs. For instance, a pattern might involve both rotation and scaling, where shapes not only turn but also change size as they progress. The golden spiral, found in nautilus shells and galaxy formations, is a prime example of a pattern that combines rotation and scaling.
To analyze patterns with multiple rules or transformations, break down the pattern into its component parts. Identify the basic shapes or elements, then observe how they change through each transformation. Look for repeating units or modules that make up the larger pattern. It's often helpful to sketch or diagram the pattern, highlighting the transformations at each step.
Creating advanced patterns requires a systematic approach. Start by defining your basic elements and the transformations you want to apply. Experiment with different combinations of rotations, reflections, and scaling. Use grid paper or digital design tools to maintain precision in your patterns. Remember that even complex patterns often have a simple underlying structure or rule set.
Here's a challenging example to consider: Imagine a pattern that starts with a square. In each iteration, the square is rotated 45 degrees, scaled to 75% of its original size, and then reflected across a diagonal axis. How would this pattern evolve over several iterations? Try sketching this out to visualize the transformation sequence.
Another exercise to enhance your pattern recognition skills is to analyze tessellations, which are patterns that fill a plane with no gaps or overlaps. M.C. Escher's artworks are famous for their complex tessellations involving interlocking shapes and creatures. Try to identify the basic shape in an Escher tessellation and describe the transformations applied to create the overall pattern.
Advanced pattern recognition also plays a crucial role in various fields beyond art and mathematics. In computer vision and machine learning, algorithms are designed to recognize complex patterns in images or data sets. These might involve identifying rotated or scaled versions of objects in photographs or detecting subtle patterns in large datasets.
To further challenge yourself, try creating a pattern that incorporates all three transformations - rotation, reflection, and scaling - in a single, cohesive design. Start with a simple geometric shape and apply each transformation sequentially. How does the pattern change with each iteration? Can you predict what it will look like after several cycles?
As you explore these advanced concepts, remember that pattern recognition is as much an art as it is a science. While there are mathematical principles underlying many patterns, the ability to perceive and create complex patterns also relies on intuition and creativity. Practice regularly by observing patterns in nature, architecture, and art, and try to deconstruct them into their basic elements and transformations.
In conclusion, mastering advanced pattern recognition and creation opens up a world of possibilities in design, problem-solving, and analytical thinking. By understanding and applying concepts of rotation, reflection, and scaling, you can uncover hidden structures in the world around you and create intricate, beautiful patterns of your own. Continue to challenge yourself with complex examples and exercises, and you'll develop a keen eye for patterns that
Conclusion
Patterns with shapes are fundamental to mathematical thinking and problem-solving. The introduction video provides a crucial foundation for understanding this concept, highlighting key aspects of pattern recognition and shape analysis. By exploring various geometric arrangements, students develop critical observation skills and learn to identify recurring elements. This ability to recognize and extend patterns is essential in mathematics and beyond. As you continue your journey, practice creating and analyzing patterns with different shapes, sizes, and orientations. Remember, pattern recognition is a skill that improves with experience. Challenge yourself to find patterns in everyday objects and situations, applying the principles learned here. Don't hesitate to revisit the introduction video for reinforcement. By mastering patterns with shapes, you're building a strong foundation for advanced mathematical concepts. Keep exploring, questioning, and discovering the fascinating world of patterns your mathematical thinking will flourish as a result!
Introduction to Patterns with Shapes: What are shape patterns?
In this lesson, we'll be talking about patterns with shapes. Understanding shape patterns is essential as it helps in recognizing and predicting sequences in various contexts. Let's dive into the concept of shape patterns step by step.
Step 1: Understanding Patterns
A pattern is something that repeats over and over again. Patterns can be visual, meaning they can be seen and recognized easily. Because patterns repeat, they allow us to predict what comes next. This predictability is a key feature of patterns.
Step 2: Examples of Patterns
Patterns can be created using various elements such as numbers, letters, objects, and shapes. Here are a few examples:
- Numbers: A sequence like 1, 2, 3, 1, 2, 3 is a pattern where the numbers 1, 2, and 3 repeat.
- Letters: A sequence like A, B, A, A, B, A shows a repeating pattern of letters.
- Objects: A sequence of fruits like banana, strawberry, banana, strawberry is a pattern where the fruits alternate.
- Shapes and Colors: A sequence of shapes like blue rectangle, purple rectangle, purple rectangle, blue rectangle, purple rectangle, purple rectangle shows a pattern where the colors of the rectangles alternate.
Step 3: Focusing on Shape Patterns
For this section, we will focus on patterns with shapes. The principles remain the same: we look for repeated segments within the sequence of shapes. Each shape in the pattern is part of a repeating segment, and by identifying this segment, we can predict the next shape in the sequence.
Step 4: Simple Shape Patterns
Let's start with a simple pattern involving two shapes. For example, a sequence of a triangle followed by a square. The pattern would look like this: triangle, square, triangle, square, and so on. By copying and pasting this segment, we can extend the pattern indefinitely. The next shape in this pattern would be a triangle.
Step 5: More Complex Shape Patterns
Patterns can also be more complex, involving more than two shapes. For instance, a pattern could include four shapes: square, triangle, circle, and diamond. The sequence would be: square, triangle, circle, diamond, square, triangle, circle, diamond, and so on. By identifying the repeating segment, we can predict that the next shape in this pattern would be a square.
Step 6: Practical Application of Shape Patterns
Understanding and recognizing shape patterns is useful in various fields such as mathematics, art, and design. It helps in developing problem-solving skills and logical thinking. By practicing with different types of patterns, one can become proficient in identifying and predicting sequences.
Conclusion
In summary, shape patterns are sequences where shapes repeat in a predictable manner. By understanding the concept of repetition and identifying the repeating segments, we can easily predict the next elements in the pattern. This knowledge is not only useful in academic contexts but also in everyday problem-solving scenarios.
FAQs
-
What are the basic shapes used in pattern creation?
The basic shapes commonly used in pattern creation include circles, squares, triangles, rectangles, and hexagons. These simple geometric forms serve as the building blocks for more complex patterns. By combining and arranging these shapes in various ways, you can create an infinite variety of patterns.
-
How can I identify the repeating segment in a pattern?
To identify the repeating segment in a pattern, follow these steps: 1) Look at the beginning of the pattern. 2) Try to find where the sequence starts to repeat. 3) Check if this sequence continues throughout the pattern. 4) If it does, you've found the repeating segment. Practice with simple patterns first, then move on to more complex ones as you improve your skills.
-
What is a compound shape in pattern creation?
A compound shape is formed by combining two or more simple shapes to create a more intricate figure. For example, you might start with a square and add triangles to each side to form a star-like shape. Compound shapes are used to create more complex and visually interesting patterns, often serving as the basis for further additions and variations in pattern sequences.
-
How can I analyze patterns numerically?
To analyze patterns numerically, you can: 1) Count the number of each type of shape in each iteration. 2) Measure the perimeter or area of the compound shape as it grows. 3) Calculate the ratio between different elements of the pattern. 4) Identify recurring numerical patterns in the sequence of shapes. This analysis can help you discover mathematical relationships and predict future iterations of the pattern.
-
What are some advanced techniques in pattern creation?
Advanced techniques in pattern creation include rotation, reflection, and scaling of shapes. Rotation involves turning shapes around a central point, reflection creates mirror images across an axis, and scaling changes the size of shapes while maintaining proportions. These transformations can be combined to create complex, visually striking designs. Tessellations, which fill a plane with no gaps or overlaps, are another advanced pattern technique worth exploring.
Prerequisite Topics
Understanding patterns with shapes is a fundamental concept in mathematics that builds upon several basic skills and knowledge areas. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in basic geometry, spatial reasoning, and pattern recognition is essential for mastering patterns with shapes.
Geometry forms the backbone of understanding shapes and their properties. Students should be familiar with basic geometric concepts such as identifying different types of shapes, understanding their attributes, and recognizing how shapes can be combined or manipulated. This foundational knowledge allows students to better comprehend how patterns can be created and extended using various shapes.
Spatial reasoning skills play a crucial role in visualizing and manipulating shapes mentally. This ability helps students identify relationships between different shapes and how they fit together to form patterns. Developing strong spatial reasoning skills enables students to predict how patterns will continue or change based on given rules or sequences.
Pattern recognition is another key skill that directly relates to understanding patterns with shapes. Students should be able to identify repeating elements, sequences, and rules that govern how shapes are arranged in a pattern. This skill is not only important for mathematics but also has applications in various other fields and everyday life situations.
Basic counting and number sense are also relevant prerequisites, as they help students understand the repetition and sequencing involved in patterns. Being able to count and recognize numerical patterns can assist in identifying and creating shape patterns.
Additionally, a basic understanding of symmetry can be beneficial when working with shape patterns. Many patterns involve symmetrical arrangements, and recognizing this concept can help students create and analyze more complex patterns.
While these topics may not be formally listed as prerequisites, they form the essential building blocks for understanding patterns with shapes. Teachers and students should ensure a solid grasp of these fundamental concepts to facilitate a smoother learning experience when delving into more advanced pattern work.
By developing these foundational skills, students will be better equipped to explore the fascinating world of patterns with shapes. They'll be able to recognize, create, and extend patterns more easily, leading to a deeper understanding of mathematical concepts and improved problem-solving abilities.
As students progress in their study of patterns with shapes, they'll find that this knowledge connects to more advanced mathematical concepts, such as algebra, tessellations, and even aspects of computer science and art. The skills developed through working with shape patterns can enhance logical thinking and creativity, making it a valuable area of study with wide-ranging applications.

