Properties of scalar multiplication
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
In this lesson, we will look at the properties of matrix scalar multiplication. These properties include the dimension property for scalar multiplication, associative property, and distributive property. The dimension property states that multiplying a scalar with a matrix (call it A) will give another matrix that has the same dimensions as A. For the associative property, changing the order in which you multiple the matrices has no effect on the final computation. The distributive property states that a scalar can be distributed to the addition or subtraction of matrices. The addition or subtraction of scalars can also be distributed to a matrix. Lastly, we will learn that there is a multiplication property for zero matrices. This property states that multiplying a zero scalar with a matrix will result in a zero matrix. In addition, any scalar multiplied by a zero matrix will result in a zero matrix.
Properties of scalar multiplication
During our lesson about scalar multiplication, we talked about the big differences between this kind of operation and the matrix multiplication. Now it is time to look in details at the properties this simple, yet important, operation applies.
What is a scalar multiplication
Given that a scalar multiplication is a very simple operation and we have already discussed it before, this section may seem a little redundant but we are keeping so you dont have to be clicking back and forth between this and past lessons if you ever want to see the basic concepts. The scalar multiplication refers to the operation in which a real number multiplies an algebraic object such as a vector or a matrix. We are of course, focused on the cases multiplying scalars and matrices together given that we are working on operations with matrices.Remember that a scalar is a real number that multiplied to a vector space it resizes the vector (changes its magnitude) without affecting its direction. The name scalar comes from that particular operation because multiplying a real number by a vector re-scales the vector without changing other of its main characteristics, such as direction and dimensions. But as we have said it, we are interested on the case in which a scalar multiplies a matrix.
And so, a scalar multiplication of a matrix happens to produce a similar effect when compared to the multiplication of a scalar and a vector. The operation of the multiplication of a matrix by a real number produces a matrix which keeps its main properties such as: order, linear dependence, proportion between its elements and equivalency between sets of linear equations that may conform it.
Since a matrix is an array of numbers which can be thought of an array of ordered vectors (either column vectors or row vectors). We can use that relationship and see that a matrix multiplication by scalar numbers results in an array (the resulting matrix) of ordered vectors which have had a change in magnitude (just as multiplying an isolated vector by a scalar) but they still keep the proportion between its different variable coefficients, or in other words, they keep the same direction they would have if graphed in euclidean coordinate planes.
In conclusion, scalar multiplication happens to be one of the easiest, if not the most, of all matrix operations of an external nature that can be done. And the notation of it has the form of:
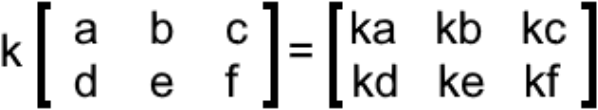
Properties of scalar multiplication of matrices
If we define two matrices of any order (but equal among them) to be X and Y, and then define c and d to be scalar, we can describe the following scalar multiplication properties:1. Dimension property for scalar multiplication
When performing a multiplication of a matrix by a scalar, the resulting matrix will always have the same dimensions as the original matrix in the multiplication. For example, if we multiply c⋅X the matrix that results from it has the dimensions of X.
This makes complete sense if you look at equation 1, the only thing that it is done in a scalar multiplication of matrices is to multiply each of the components of the matrix by the scalar outside, there is no added feature, and so, the elements remain in their place and the result is a matrix of the same size.
2. Commutative property
While performing the multiplication of a matrix times a scalar, the order in which the factors are arranged in the operation makes no difference in the result. In other words, if we are to calculate the scalar and matrix multiplication of c and X or d and Y the result of these operations does not change, no matter how you arrange the operations. Simply said: c⋅X=X⋅c and d⋅Y=Y⋅d.
If we define the matrix X to be:
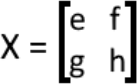
Then the commutative property tells us that:
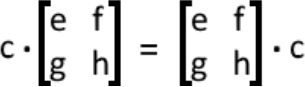
3. Associative property
The associative property gives the opportunity to perform a long scalar multiplication in steps. What the associative property tells us is that even if you have many factors involved, for this case many scalar times a matrix, you can select to perform the multiplication among two of the factors first and then use the result of that operation to multiply for another factor that has not been used and repeat this process until you are done multiplying all of the factors in the multiplication to obtain the result.
Let us give a brief example: let us say you are multiplying bot scalars c and d times matrix X. The associative property gives the opportunity to select two of these factors (c, d and X) and multiply them first, then using the result of that, multiply it by the factor that is left and obtain the result, rather than perform the two multiplications at the same time (which could get complicated if more than three factors are present). In simple terms, the associative property says that: c⋅d⋅X=c⋅(dX)=d⋅(cX)=(dc)X
4. Distributive property
The distributive property comes to place when the operation of the scalar multiplication of a matrix comes in combination with another arithmetic operation, such as addition or subtraction. In other words, we use the distributive property to simplify problems in which one of the factors in the scalar matrix multiplication is an addition or a subtraction.
Mathematically speaking the distributive properties of matrix multiplication defines that if one of the factors in the multiplication is an addition of two matrices, then: c⋅(X+Y)=cX+cY.
On the other hand, if one of the factors in the multiplication is an addition of scalars, the distributive property says that: (c+d)X=cX+dX
5. Multiplication property for the zero matrix
This property describes that as long as the result of a multiplication by the zero matrix is defined, meaning that as long as the multiplication can be performed following all of the necessary dimension conditions, the result of such multiplication will always be the zero matrix itself, it doesnt matter if it's the product of a scalar and a matrix (in which case the matrix would be the zero matrix), or the product of two matrices (one of them being the zero matrix).
Since all of the elements of a zero matrix are zeros, no matter which scalar you multiply to them, the scalar multiplication matrix will turn to have all entries equal to the results of a multiplication by zero, which is zero. And so, multiplying by the zero matrix always produces a zero matrix result.
Therefore, if we perform the scalar multiplication of matrix 0 it follows that: c⋅0=0.
Example:
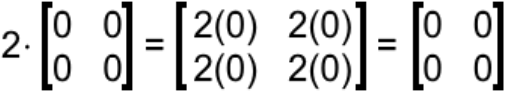
In here, the matrix multiplication of scalar 2 makes no difference if it was any other scalar, since it will multiply by all zero entries, producing again all zeros.
The same goes if you multiply the zero matrix times another matrix: 0⋅X=0.
Before we continue onto the next section, notice that the properties of matrix addition and scalar multiplication are very similar, which makes them easy to remember and understand. Once you have practiced enough, they will come naturally to you and we recommend you to come back to these lessons and see all of the other ways (different order of steps, or other usage of the properties described above) in which you can solve the exercises e provide, you know, just for the fun of math!
Properties of scalar multiplication examples
Let us put into practice the knowledge gained about the properties of matrix scalar multiplication and solve the next example exercises.
Example 1
Making use of the scalar multiplication properties of matrices seen above, show the scalar multiplications of zero or one, with any matrix, produce zero (for multiplication by zero), or the same matrix (for multiplication by 1) as seen in the equations given in parts a) and b).Use matrix A as defined below to prove our statement.
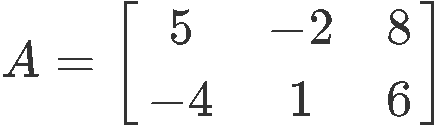
a) Prove that 0⋅A=0
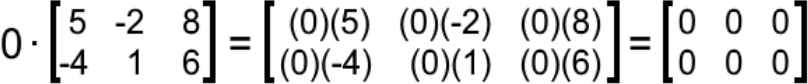
And so, as you can see here, the scalar multiplication by a zero results in a zero matrix of the same dimensions as the original matrix. Since the matrix multiplying the zero scalar has the dimensions of 2 × 3 in this case, the resulting matrix has dimensions of 2 × 3 too.
b) Prove that 1⋅A=A
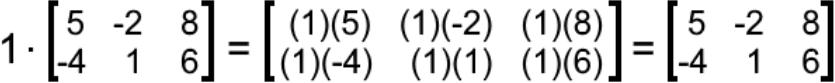
As observed above, we have proved that any matrix multiplying the scalar one will result in the same matrix.
Example 2
Using the following given matrices: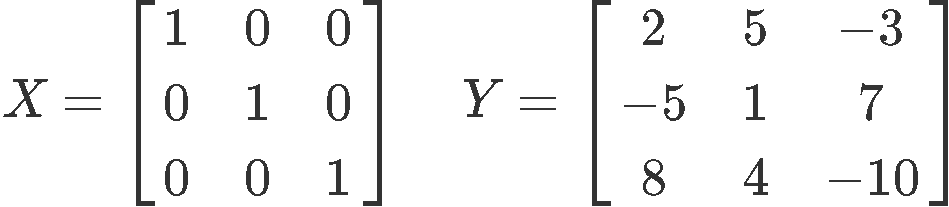
And scalars c=5 and d=3. Show that the following equations hold true due to the scalar multiplication properties of matrices:
a) c(X+Y)=cX+cY
The equation above defines the first distributive property described in the last section of this lesson. Using the 3x3 matrices X and Y, we can observe scalar multiplication is distributive and follows this equation by working each side and comparing the results obtained from each of them.
In order to solve this problem, we will make use of what we know about adding and subtracting matrices from past lessons. To start, we solve the left hand side of the equation: c(X+Y)
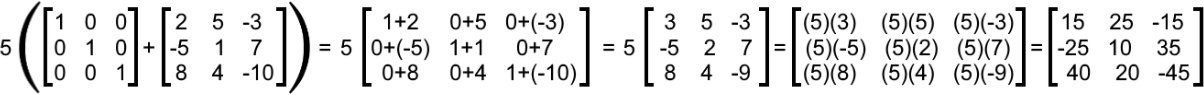
Solving the right hand side of the equation: cX+cY

As you can see, both sides yield the same result, and so, the distributive property shown is proved.
b) (c+d)Y=cY+dY
This particular equation defines the second distributive property explained in the second section of this lesson. Just as before, in order to prove the equation holds true we solve each side of the equation separately and then compare the results. We start by solving the left hand side: (c+d)Y
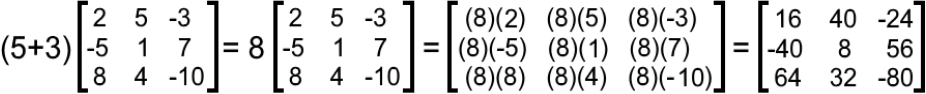
Now, computing the right hand side of the equation: cY+dY

And since both results are the same, we have proved that (c+d)Y=cY+dY
c) (c+d)(X+Y)=c(X+Y)+d(X+Y)
For this case we are once more about to prove the second distributive property of scalar matrix multiplication, the only difference is that instead of multiplying the addition of two scalars to an already defined matrix, we are now multiplying it to the matrix resulting from the addition of X and Y. Remember that when adding matrices the resulting one must have the same dimensions than the matrices it comes from, and therefore, the matrix X+Y happens to be:
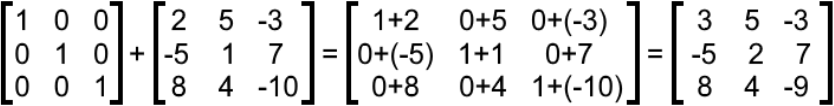
With that in mind, we verify the equation given in c) through the same process done in parts a) and b): we solve the left hand side of the equation first, then the right hand side, and finally compare the results of both. We start with the left hand side (c+d)(X+Y):
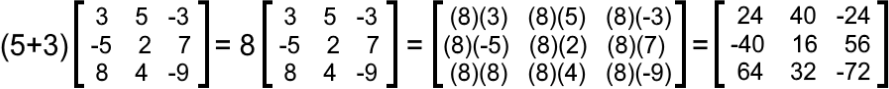
Solving the right hand side c(X+Y)+d(X+Y):

As you can see, the resulting matrix is the same for both sides of the equation, and so, the distributive property has been proved once more.
So this is it on the properties of scalar multiplication. An important note to remember is that the name of the properties gives major hints on their usage: commutative talks about the ability to move the factors in the multiplication; associative means you can put together a few of them to then keep on operating; distributive says you can distribute one factor among others and all of this without affecting the final result.
If you would like to continue studying the properties of scalar multiplication of matrix X and a scalar (we use matrix X meaning any matrix), we recommend you the next link on the multiplication of a matrix by a scalar which contains a few more examples on the topic.
See you in our next lesson!
Note
Let X,Y be matrices with equal dimensions, and c and d be scalars. Then we have the following scalar multiplication properties:
Dimension property for scalar multiplication
The matrix c⋅X has the same dimensions as X.
Associative property
c⋅X=X⋅c
c⋅(dX)=d⋅(cX)=(dc)X
Distributive property
c(X+Y)=cX+cY
(c+d)X=cX+dX
There are also some scalar multiplication properties with the zero matrix
Multiplication property for the zero matrix
0⋅X=O
c⋅O=O
Let X,Y be matrices with equal dimensions, and c and d be scalars. Then we have the following scalar multiplication properties:
Dimension property for scalar multiplication
The matrix c⋅X has the same dimensions as X.
Associative property
c⋅X=X⋅c
c⋅(dX)=d⋅(cX)=(dc)X
Distributive property
c(X+Y)=cX+cY
(c+d)X=cX+dX
There are also some scalar multiplication properties with the zero matrix
Multiplication property for the zero matrix
0⋅X=O
c⋅O=O
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today

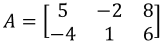 . Show that the following is true:
. Show that the following is true: 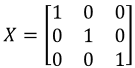 ,
, 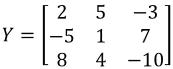 ,
, 

