Points, lines, line segments, and rays
Topic Notes
In this lesson, we will learn:
Notes:
- Points, Lines, Line Segments and Rays are basic figures in math that can be used to construct more complicated figures (i.e. angles, shapes, parallel/perpendicular lines, etc.)

- A point is a dot with position but no size nor shape (undefined)
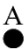
- There are an infinite number of points in figures (i.e. you can draw many points between endpoints in a line segment)

- The proper notation of a point is just to write the named letter (ex. point )
- A line has no beginning/end; an ongoing straight path of points

- The arrows on both sides mean that it can extend infinitely in that direction
- The proper notation of a line is to write the letters of two points in the figure and draw a double-sided arrow above the letters (ex. line )
- A line segment is a part of a line with two finite endpoints

- A line has arrows on both ends whereas the line segment has endpoints on both ends; the line continues forever, where the line segment ends where it is drawn
- The proper notation of a line segment is to write the letters of the two endpoints and draw a bar above the letters (ex. line segment )
- A ray starts at one endpoint and extends in one direction

- One end of the ray has a point, whereas the other end of the ray has an arrow
- The proper notation of a ray is to write the letters of two points in the figure (starting with the letter of the endpoint) and draw a one-sided arrow above the letters (ex. ray )
Introduction to Basic Geometric Figures
Points, lines, line segments, and rays are the fundamental building blocks of geometry. The introduction video provides a crucial overview of these basic geometric figures, laying the groundwork for understanding more complex concepts. Points are precise locations in space, while lines extend infinitely in both directions. Line segments are portions of lines with defined endpoints, and rays have a starting point but extend infinitely in one direction. These concepts are essential for grasping more advanced geometric ideas and shapes. By mastering these basic elements, students can develop a strong foundation for exploring topics like angles, polygons, and three-dimensional figures. The video presentation offers clear explanations and visual representations, making it easier for learners to grasp these abstract concepts. As you progress in your geometry studies, you'll find that these basic figures are constantly referenced and applied, underscoring their importance in the field of mathematics.
Points: The Foundation of Geometry
In geometry, a point is a fundamental concept that serves as the building block for all other geometric figures. A point is defined as a precise location in space, having position but no size or shape. It is essentially a zero-dimensional object, meaning it has no length, width, or height. Points are the most basic elements in geometry, from which we construct more complex shapes and figures.
One of the key characteristics of a point is that it has position but no magnitude. This means that while we can identify where a point is located, it doesn't occupy any space. To visualize this, imagine a dot on a piece of paper. While we can see the dot, in geometric terms, a true point would be infinitely small, with no area or volume.
In geometric notation, points are typically named using uppercase letters. For example, we might refer to Point A, Point B, or Point C. This naming convention allows mathematicians and students to easily reference specific points when discussing or solving geometric problems. When multiple points are involved, it's common to use consecutive letters of the alphabet, such as Points A, B, and C, or Points P, Q, and R.
Points play a crucial role in various geometric figures. For instance, in a line segment, points mark the endpoints. In a triangle, points represent the vertices where the sides meet. In a circle, the center is a point, and any location on the circumference is also considered a point. Even in three-dimensional shapes like cubes or spheres, points are used to define corners, centers, and other key locations.
One of the most fascinating aspects of points in geometry is the concept of infinite points. Between any two points on a line or within a geometric figure, there are infinitely many other points. This idea is crucial in understanding continuity in mathematics and forms the basis for more advanced concepts in calculus and analysis. For example, on a line segment between Point A and Point B, we can always find another point halfway between them, and then another point halfway between those, and so on, ad infinitum.
Understanding points is essential for grasping more complex geometric concepts. They form the basis for lines, planes, and all other geometric shapes. By mastering the concept of points, students lay the groundwork for exploring the rich world of geometry and its applications in various fields, from architecture to physics and beyond.
Lines: Extending Infinitely
In geometry, a line is defined as a straight path of points that extends infinitely in both directions. This fundamental concept forms the basis for many geometric principles and real-world applications. Understanding lines and how to represent them is crucial in mathematics and various fields of study.
One of the key characteristics of a line is its infinite nature. Unlike line segments, which have definite endpoints, a line continues endlessly in both directions. This concept can be challenging to visualize, as we often encounter limited representations of lines in our everyday lives.
When it comes to naming lines, mathematicians and students use a specific notation involving two points on the line. To name a line, we select any two distinct points on that line and use their labels. For example, if we have two points A and B on a line, we can refer to that line as "line AB" or "line BA." The order of the points doesn't matter, as the line extends infinitely in both directions.
The proper notation for representing a line uses a double-sided arrow () placed above the two point labels. For instance, the line passing through points A and B would be written as AB or BA. This double-sided arrow emphasizes the infinite nature of the line, extending beyond the two points in both directions.
It's important to note that while we use two points to name and represent a line, a line actually contains an infinite number of points. Between any two points on a line, no matter how close they are, there are always infinitely many more points. This concept of density is a fundamental property of lines and contributes to their continuous nature.
In geometry, lines play a crucial role in various contexts. They form the edges of polygons, serve as the basis for measuring angles, and are essential in constructing more complex geometric shapes. Lines are also used to define important concepts such as parallel and perpendicular relationships between geometric objects.
The applications of lines in real-world extend far beyond the realm of pure mathematics. In the real world, we encounter lines in numerous situations. For example:
- Architecture and construction: Straight lines are essential in designing and building structures, ensuring proper alignment and stability.
- Transportation: Roads, railway tracks, and flight paths often follow straight lines to provide the most efficient routes.
- Art and design: Artists and designers use lines to create perspective, define shapes, and guide the viewer's eye.
- Physics: Light travels in straight lines, forming the basis for optics and many optical devices.
- Surveying and cartography: Lines are used to measure distances and create accurate maps of land and terrain.
Understanding the concept of lines as infinite entities helps us grasp more advanced geometric principles and their applications in various fields. Whether we're solving mathematical problems, designing structures, or navigating through space, the fundamental properties of lines continue to play a crucial role in our understanding of the world around us.
As we delve deeper into geometry and its applications, the concept of lines serves as a foundation for more complex ideas. From parallel and perpendicular relationships to the study of curves and non-Euclidean geometries, our understanding of lines provides a starting point for exploring the rich and diverse world of mathematical shapes and spatial relationships.
Line Segments: Finite Portions of Lines
Line segments are fundamental elements in geometry, representing finite portions of a line with two distinct endpoints. Unlike lines that extend infinitely in both directions, line segments have a definite beginning and end. This characteristic makes line segments essential in various geometric constructions and real-world applications.
To properly identify and discuss line segments, it's crucial to understand their naming convention. Line segments are typically named using the two points that serve as their endpoints. The standard notation involves writing the two endpoint letters with a bar above them. For example, if a line segment has endpoints A and B, it would be written as AB̅ (with a bar over AB). This notation clearly distinguishes line segments from lines or rays.
Line segments are ubiquitous in geometric shapes. In triangles, for instance, each side is a line segment. Consider a triangle ABC; its three sides are the line segments AB̅, BC̅, and CA̅. Similarly, in other polygons like squares, rectangles, or pentagons, each side is represented by a line segment. This concept extends to three-dimensional shapes as well, where edges of solids like cubes or pyramids are line segments.
The distinction between lines and line segments is crucial in geometry. While a line extends infinitely in both directions, a line segment has definite start and end points. This difference impacts various geometric properties and calculations. For example, lines have infinite length, whereas line segments have a measurable, finite length. This finite nature of line segments allows for precise measurements and comparisons in geometric problems and real-world applications.
In practical terms, line segments are more commonly encountered in everyday life than infinite lines. The edge of a table, the length of a pencil, or the distance between two cities on a map are all represented by line segments. This practicality makes line segments a crucial concept in fields ranging from architecture and engineering to computer graphics and design.
Understanding line segments is also essential for more advanced geometric concepts. They form the basis for studying angles, as angles are often formed by the intersection of two line segments. In coordinate geometry, line segments play a vital role in plotting and analyzing shapes on a coordinate plane. The concept of midpoints, which is the point that divides a line segment into two equal parts, is another important application of line segments in geometry.
Line segments also introduce the concept of length in geometry. The length of a line segment is the distance between its two endpoints. This concept is fundamental in various mathematical calculations and real-world measurements. In more advanced mathematics, the properties of line segments, such as their ability to be bisected or trisected, lead to important theorems and problem-solving techniques.
In conclusion, line segments are essential components of geometry, representing finite portions of lines with two definite endpoints. Their proper notation and naming convention using endpoint letters with an overbar distinguish them from infinite lines. Found in various geometric shapes and everyday objects, line segments bridge the gap between abstract geometric concepts and practical applications. Understanding the difference between lines and line segments is crucial for grasping more complex geometric principles and solving real-world problems involving measurements and spatial relationships.
Rays: One Endpoint, One Direction
In geometry, a ray is a fundamental concept that plays a crucial role in understanding various shapes and figures. A ray is defined as a part of a line that has one fixed endpoint and extends infinitely in one direction. This unique characteristic distinguishes rays from other linear elements in geometry, such as lines and line segments.
Naming rays is an essential skill in geometry. To properly identify a ray, we use two points: the endpoint and any other point along the ray's path. The convention for naming a ray is to use the endpoint first, followed by another point on the ray. For example, if we have a ray with endpoint A that passes through point B, we would name it "ray AB." The proper notation for a ray uses a one-sided arrow above the two letters, indicating the direction of the ray's infinite extension.
Rays are commonly encountered in various geometric contexts, with angles being one of the most prominent examples. An angle is formed by two rays that share a common endpoint, called the vertex. For instance, in an angle ABC, ray BA and ray BC form the two sides of the angle, with point B serving as the vertex. This application of rays in angles is fundamental to trigonometry and many other areas of mathematics.
It's important to distinguish rays from other linear elements in geometry. While a ray has one endpoint and extends infinitely in one direction, a line extends infinitely in both directions and has no endpoints. A line segment, on the other hand, has two distinct endpoints and a finite length. Understanding these differences is crucial for solving geometric problems and constructing accurate diagrams.
Rays also play a significant role in other geometric concepts. For example, they are used to define half-planes, which are created when a line divides a plane into two regions. Additionally, rays are essential in describing the behavior of light in optics, where they represent the path of light traveling in a straight line from a source.
In practical applications, rays can be used to model various real-world phenomena. For instance, in navigation, a ray can represent the direction of travel from a starting point. In physics, rays are used to describe the propagation of waves, such as sound or electromagnetic radiation. Understanding rays and their properties is therefore not only important in pure mathematics but also in applied sciences and engineering.
To visualize rays, it's helpful to think of them as beams of light emanating from a single point source. This analogy captures the essence of a ray's definition: a fixed starting point with an infinite extension in one direction. When working with rays in geometric constructions or proofs, it's crucial to remember that while the endpoint is fixed, the ray itself continues indefinitely.
In conclusion, rays are essential elements in geometry, characterized by their single endpoint and infinite extension in one direction. Proper naming and notation of rays, using two points and a one-sided arrow, are crucial for clear communication in mathematical contexts. Their applications in angles, geometric constructions, and real-world modeling make rays a fundamental concept to master in the study of geometry and related fields.
Intersecting Figures
Intersecting figures are a fundamental concept in geometry, involving the meeting or crossing of two or more geometric shapes. The point where these figures meet is called the intersection point. Understanding intersecting figures is crucial for solving various geometric problems and real-world applications.
Let's explore the concept of intersection with different geometric elements:
1. Intersecting Lines: When two lines cross each other, they create an intersection point. This point is the only common point shared by both lines. For example, imagine two straight roads crossing each other; the point where they meet is their intersection.
2. Intersecting Line Segments: Line segments are portions of lines with defined endpoints. When two line segments cross, they form an intersection point within the boundaries of both segments. Picture two pencil lines drawn on paper that cross each other; the point where they meet is their intersection.
3. Intersecting Rays: Rays are lines that start at a point and extend infinitely in one direction. When two rays intersect, they create an intersection point. This can be visualized as two beams of light crossing each other; the point where the beams meet is their intersection.
The importance of intersection points in geometry cannot be overstated. They play a crucial role in various geometric concepts and applications:
- In coordinate geometry, intersection points help determine the solutions to systems of equations.
- Intersection points are essential in understanding and solving problems related to angles, such as vertical angles and complementary angles.
- In construction and engineering, identifying intersection points is vital for designing structures and ensuring proper alignment of components.
- Intersection points are used in computer graphics and game development to detect collisions between objects.
- In navigation and mapping, intersections of roads, rivers, or other geographical features are crucial reference points.
When working with intersecting figures, it's important to note that not all figures will necessarily intersect. Parallel lines, for instance, never intersect. Additionally, some figures may intersect at multiple points, such as a line intersecting a circle at two points.
Understanding intersecting figures and their properties is essential for developing spatial reasoning skills and solving complex geometric problems. By mastering this concept, students and professionals alike can better analyze and interpret geometric relationships in both theoretical and practical contexts.
Applications and Examples
Points, lines, line segments, and rays are fundamental geometric concepts that find numerous real-world applications in architecture, engineering, and everyday life. These basic elements serve as building blocks for more complex shapes and are essential in solving geometric problems.
In architecture, points are used to mark specific locations on blueprints and 3D models. For example, architects use points to indicate where walls intersect or where fixtures should be placed. Lines and line segments are crucial in creating floor plans, outlining walls, and defining boundaries. The concept of rays is applied in designing roof slopes and calculating sun angles for optimal natural lighting.
Engineering relies heavily on these geometric figures. Civil engineers use points to mark survey locations and plot coordinates for construction projects. Lines and line segments are essential in designing roads, bridges, and pipelines. Mechanical engineers employ these concepts in creating technical drawings and designing machine parts. Rays are particularly useful in optics and laser technology, where they represent the path of light.
In everyday life, we encounter these geometric elements constantly. Street intersections can be viewed as points, while roads themselves are excellent examples of lines and line segments. The edges of tables, doors, and windows are all line segments. Rays can be observed in the beams of flashlights or the trajectory of a thrown ball before it begins to fall.
These basic figures are used to construct more complex shapes. For instance, connecting multiple line segments creates polygons, which form the basis of many structures and objects. Circles are defined by points equidistant from a center point. In computer graphics and digital design, these elements are the foundation for creating intricate images and 3D models.
Geometric problems often involve manipulating these basic elements. For example, finding the intersection of two lines is crucial in navigation and GPS technology. Calculating the distance between two points is essential in mapping and logistics. Understanding the properties of parallel and perpendicular lines is vital in construction and manufacturing to ensure structural integrity and precision.
In the field of astronomy, rays are used to represent the path of light from distant stars, while points mark the position of celestial bodies. Geologists use lines and line segments to represent fault lines and rock strata. In the world of art and design, these geometric elements form the basis of perspective drawing and composition.
By understanding and applying these fundamental geometric concepts, professionals across various fields can solve complex problems, create innovative designs, and improve the world around us. From the grandest architectural marvels to the simplest everyday objects, points, lines, line segments, and rays play an indispensable role in shaping our environment and advancing technology.
Conclusion
In summary, understanding points, lines, line segments, and rays is crucial for mastering basic geometric figures. Points are precise locations in space, while lines extend infinitely in both directions. Line segments have definite endpoints, and rays start at a point and extend infinitely in one direction. These fundamental concepts form the building blocks for more advanced geometric principles. Grasping these basics is essential for progressing in geometry and related fields. If you're still unsure about any of these concepts, we encourage you to rewatch the introduction video. To reinforce your learning, try identifying these geometric figures in your everyday surroundings. Look for examples of points, lines, line segments, and rays in architecture, nature, or household objects. This practical application will help solidify your understanding and prepare you for more complex geometric challenges ahead. Remember, a strong foundation in these basic geometric figures is key to success in more advanced mathematical concepts.
Introduction to Points, Lines, Line Segments, and Rays
In this guide, we will explore the fundamental concepts of points, lines, line segments, and rays. These basic figures are essential in understanding more complex geometric concepts and are widely used in various mathematical applications.
Step 1: Understanding Points
A point is a fundamental concept in geometry. It is represented as a dot on a page and signifies a specific position. However, a point does not have any size or shape. It is simply a location. For example, you might place a dot on the upper left corner of a page, but you cannot measure its size in centimeters or any other unit. Points are often labeled with letters, such as point A, to identify them in diagrams and problems.
Points can exist anywhere on a figure, such as on a line, a shape, or a grid. They are used to mark specific locations, such as the start and end points of a line segment. Importantly, there are an infinite number of points between any two endpoints on a figure, meaning you can always find more points by zooming in and examining the figure more closely.
Step 2: Defining Lines
A line is a straight one-dimensional figure that extends infinitely in both directions. It is composed of an infinite number of points. Lines are usually represented with arrows on both ends to indicate that they extend without end. In diagrams, lines are often labeled with lowercase letters or by naming two points on the line, such as line AB.
Lines are crucial in geometry as they form the basis for creating angles, shapes, and other geometric figures. They are also used to determine relationships such as parallelism and perpendicularity between different lines.
Step 3: Exploring Line Segments
A line segment is a part of a line that has two endpoints. Unlike a line, a line segment does not extend infinitely. It has a definite length that can be measured. Line segments are often used to construct shapes and polygons. For example, a triangle is made up of three line segments.
In diagrams, line segments are labeled by their endpoints. For instance, a line segment with endpoints A and B is referred to as segment AB. Line segments are fundamental in understanding the properties of shapes and in performing various geometric constructions.
Step 4: Understanding Rays
A ray is a part of a line that starts at a specific point and extends infinitely in one direction. It has one endpoint, known as the origin, and continues without end in the other direction. Rays are often used to represent directions and angles in geometry.
In diagrams, rays are labeled by their origin and another point on the ray. For example, a ray starting at point A and passing through point B is referred to as ray AB. Rays are essential in defining angles and in various geometric constructions.
Step 5: Applications and Importance
Points, lines, line segments, and rays are the building blocks of geometry. They are used to create and understand more complex figures such as angles, shapes, and polygons. These basic figures are also crucial in coordinate geometry, where they help in graphing equations and understanding the relationships between different geometric entities.
Understanding these basic figures is essential for solving problems related to parallel and perpendicular lines, constructing geometric shapes, and performing various geometric transformations. They also play a significant role in real-world applications, such as in engineering, architecture, and computer graphics.
Step 6: Summary and Review
In summary, points, lines, line segments, and rays are fundamental concepts in geometry. A point is a location without size or shape, a line extends infinitely in both directions, a line segment has two endpoints and a definite length, and a ray starts at a point and extends infinitely in one direction. These basic figures are essential for constructing and understanding more complex geometric concepts and have numerous applications in various fields.
By mastering these basic figures, you will be well-equipped to tackle more advanced topics in geometry and apply these concepts in practical situations.
FAQs
-
What is the difference between a line and a line segment?
A line extends infinitely in both directions, while a line segment has two definite endpoints. For example, a line can be represented as AB, extending infinitely beyond points A and B. A line segment, represented as AB̅, has a finite length between points A and B.
-
How are rays different from lines and line segments?
A ray has one fixed endpoint and extends infinitely in one direction. It's different from a line (which extends infinitely in both directions) and a line segment (which has two endpoints). A ray is typically represented with an arrow, like AB, where A is the endpoint and B is any point on the ray.
-
Can two lines intersect at more than one point?
No, two distinct lines can intersect at only one point. If they appear to intersect at more than one point, they are actually the same line. However, other geometric figures like curves can intersect lines or each other at multiple points.
-
How are points used in geometry?
Points are fundamental in geometry. They represent specific locations in space and are used to define other geometric figures. Points are used to mark endpoints of line segments, vertices of polygons, centers of circles, and intersections of lines or curves. They are typically labeled with uppercase letters.
-
What are some real-world applications of these geometric concepts?
These concepts have numerous applications. In architecture, points mark specific locations on blueprints. Lines and line segments are used in road design and construction. Rays are applied in optics and lighting design. In navigation, these concepts help in determining routes and distances. Computer graphics use these elements to create complex shapes and 3D models.
Prerequisite Topics
Understanding the fundamental concepts of geometry is crucial for mastering more advanced topics in mathematics. When it comes to studying "Points, lines, line segments, and rays," it's important to recognize that these concepts form the foundation of geometric understanding. While there are no specific prerequisite topics listed for this subject, having a solid grasp of basic mathematical principles and spatial reasoning skills can greatly enhance your ability to comprehend and work with these geometric elements.
Points, lines, line segments, and rays are the building blocks of geometry, and they play a vital role in various mathematical and real-world applications. These concepts are often introduced early in geometry courses because they serve as the basis for more complex geometric shapes and relationships. By understanding these fundamental elements, students can develop a strong foundation for exploring more advanced geometric concepts and problem-solving techniques.
Although there are no direct prerequisites listed, having a good understanding of basic arithmetic and algebra can be beneficial when working with points, lines, line segments, and rays. For example, knowledge of coordinate systems and plotting points on a plane can help visualize these geometric elements in a more concrete way. Additionally, familiarity with basic measurement concepts and units can aid in understanding the properties and relationships between these geometric entities.
As you delve into the study of points, lines, line segments, and rays, you'll discover how these concepts are interconnected and how they form the basis for more complex geometric figures. Points serve as the most basic element, representing a precise location in space. Lines extend infinitely in both directions, while line segments have defined endpoints. Rays, on the other hand, have a starting point and extend infinitely in one direction.
Understanding these distinctions and their properties is essential for progressing in geometry. You'll use this knowledge to explore concepts such as angles, polygons, and three-dimensional shapes. Moreover, these fundamental geometric elements are crucial in various fields, including architecture, engineering, and computer graphics.
While there may not be specific prerequisite topics listed, developing strong spatial reasoning skills and a curious mindset can greatly enhance your understanding of points, lines, line segments, and rays. Practicing visualization exercises and working with geometric drawings can help strengthen your ability to conceptualize these elements in both two and three-dimensional spaces.
As you progress in your study of geometry, remember that mastering these fundamental concepts will provide you with a solid foundation for tackling more advanced geometric problems and applications. By thoroughly understanding points, lines, line segments, and rays, you'll be well-prepared to explore the fascinating world of geometry and its numerous real-world applications.

