Roman numerals
Topic Notes
In this lesson, we will learn:
- How to read and write Roman Numerals using addition and subtraction
Notes:
- The numbers we see in math are called Western Arabic numerals (using the digits 0 to 9)
- The ancient Romans used a different set of numeralsRoman Numerals
- There is NO Roman Numeral for zero
- We still see and use Roman Numerals (i.e. naming chemical compounds, royal names, on some clocks and buildings, in laws and contracts)
- Roman Numerals use 7 alphabetic letters as symbols to represent thousands of numbers:

- You can use the mnemonic to help you memorize: IVys XL CD-roMs
- Roman Numerals only represent the digits 1 and 5 (in different place values)
- You read Roman Numerals from left to right and calculate the value by addition or subtraction.
- Use addition if your values are decreasing OR repeating (big to small)
- ex. XXVIII = 10 + 10 + 5 + 1 + 1 + 1 = 28
- REPEATING only happens for symbols that represent a 1 digit (only I, X, C, and M are repeated)
- Symbols can only repeat 3 times maximum (only one exception: 4000 = MMMM)
- Use subtraction if your values are increasing (small to big)
- ex. IV = 1 then 5 is increasing; subtract = (5 1) = 4
- ex. IX = 1 then 10 is increasing; subtract = (10 1) = 9
- Note that Roman Numerals only use subtraction when there is a digit of 4 or 9
- Notice that:
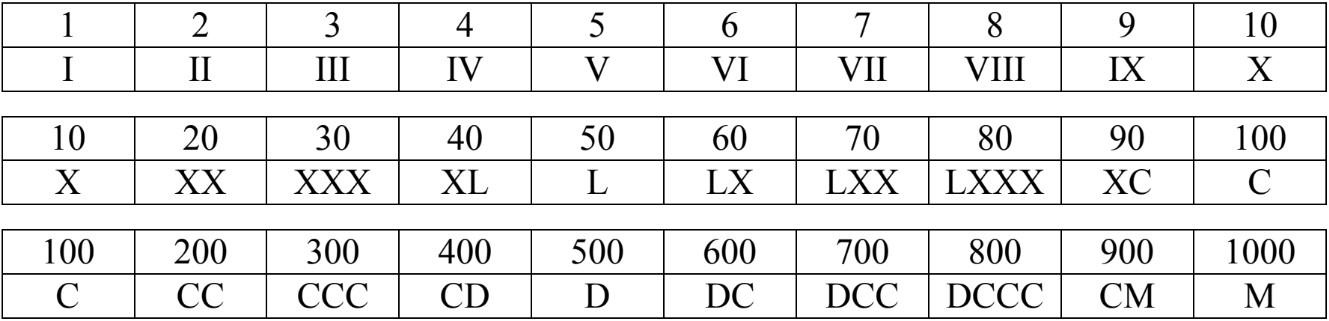
- For 1,2,3 digits: use the same power of ten symbol and repeat them
- For 4 and 9 digits: use subtraction to calculate the value
- For 5 digits: introduces a new symbol
- For 6,7,8 digits: use the power of 5 symbol, then write the power of ten symbol and repeat (just like for 1,2,3 digits)
Introduction to Roman Numerals
Welcome to our exploration of Roman numerals, an ancient number system that has stood the test of time. These fascinating symbols, originating in ancient Rome, have played a crucial role in history and continue to be relevant today. Roman numerals are a unique method of number representation, using letters to denote specific values. From clock faces to book chapters, you'll find these numerals still in use in various contexts. Our introduction video will guide you through the basics, helping you understand this intriguing system. As we delve into Roman numerals, you'll discover their historical significance and how they've influenced modern mathematics. Whether you're a history buff or a math enthusiast, learning about Roman numerals will enhance your understanding of number systems and their evolution. So, let's embark on this journey together and unravel the mysteries of this enduring ancient number system!
Understanding Roman Numeral Symbols
Roman numerals, an ancient number system still in use today, rely on a set of basic symbols to represent numerical values. These symbols are I, V, X, L, C, D, and M, each corresponding to a specific value. Understanding these symbols is crucial for decoding and using Roman numerals effectively.
Let's break down the basic Roman numeral symbols and their values:
- I represents 1
- V represents 5
- X represents 10
- L represents 50
- C represents 100
- D represents 500
- M represents 1000
To help remember these symbols and their corresponding values, a useful mnemonic device is 'IV's extra large CD-ROMs'. This phrase incorporates the symbols in order of increasing value: I (1), V (5), X (10), L (50), C (100), D (500), and M (1000).
Roman numerals represent numbers by combining these symbols according to specific rules. Unlike our modern decimal system, Roman numerals do not include a symbol for zero. Instead, they focus on additive and subtractive principles to create numbers.
The basic concept involves adding or subtracting the values of symbols to create the desired number. Generally, symbols are arranged from left to right in descending order of value. When a smaller value appears before a larger one, it indicates subtraction.
For example:
- II represents 2 (1 + 1)
- VI represents 6 (5 + 1)
- IV represents 4 (5 - 1)
- XL represents 40 (50 - 10)
- XCIX represents 99 (100 - 10 + 10 - 1)
The absence of zero in Roman numerals is a notable characteristic. This system was developed for practical counting and record-keeping, where the concept of zero as a placeholder wasn't necessary. Instead, the Romans simply didn't write anything to represent zero or none.
To illustrate how these symbols are used in more complex numbers, let's look at a few examples:
- MCMLIV represents 1954 (1000 + (1000 - 100) + 50 + (5 - 1))
- MMXXI represents 2021 (2000 + 20 + 1)
- CDXLIV represents 444 (500 - 100 + 50 - 10 + 5 - 1)
Understanding these basic symbols and their usage is essential for reading dates on buildings, chapters in books, or even deciphering historical documents. While our modern numeric system has largely replaced Roman numerals in everyday use, they continue to hold cultural and historical significance.
Mastering Roman numerals involves practice and familiarity with the symbols and their combinations. Start by memorizing the basic symbols and their values, then progress to understanding how they combine to form larger numbers. With time and practice, reading and writing Roman numerals becomes an interesting skill that connects us to ancient mathematical traditions.
Addition in Roman Numerals
Understanding addition in Roman numerals requires a different approach compared to our modern decimal system. Roman numerals are based on a left-to-right reading and follow a unique set of rules for combining symbols. Let's explore how addition works in this ancient numbering system.
First, it's crucial to understand that Roman numerals are read from left to right, with larger values typically placed before smaller ones. For example, III represents 3, and VII represents 7. This left-to-right reading is fundamental to performing addition correctly.
When adding Roman numerals, we follow these steps:
- Write out the Roman numerals for each number you want to add.
- Combine all the symbols from both numbers, maintaining their left-to-right order.
- Simplify the result by combining symbols where possible, following the rules of Roman numeral construction.
Let's look at an example: adding III (3) and VII (7).
- Write out the numbers: III and VII
- Combine the symbols: IIIVII
- Simplify: X (10)
In this case, we combined three I's (3) with a V (5) and two more I's (2), resulting in 10, which is represented by X in Roman numerals.
It's important to note the rules for repetition of symbols in Roman numerals. Only powers of 10 (I, X, C, M) can be repeated up to three times. This rule helps prevent confusion and maintains the system's readability. For example:
- III is correct (representing 3)
- IIII is incorrect (4 should be represented as IV)
- XXX is correct (representing 30)
- XXXX is incorrect (40 should be represented as XL)
The exception to this rule is the representation of 4000 and above, which traditionally used a bar over the symbol to indicate multiplication by 1000. However, for numbers below 4000, the repetition rule stands.
When adding larger numbers, the process becomes more complex but follows the same principles. For instance, adding XXVII (27) and XLIV (44):
- Write out the numbers: XXVII and XLIV
- Combine the symbols: XXVIIXLIV
- Simplify: LXXI (71)
In this case, we combined XX (20) with XL (40) to get LX (60), then added V (5) and the remaining VI (6) to reach LXXI (71).
Understanding these principles of addition in Roman numerals is essential for working with this historical numbering system. By focusing on the left-to-right reading, the concept of adding from larger to smaller values, and the rules for symbol repetition, you can confidently perform addition operations using Roman numerals.
Remember, practice is key to mastering this skill. Try adding larger numbers of Roman numerals, starting with smaller numbers and gradually increasing complexity. With time and experience, you'll find that addition in Roman numerals becomes more intuitive and manageable.
Subtraction in Roman Numerals
Welcome to the fascinating world of Roman numerals! Today, we're going to explore a special concept: subtraction in Roman numerals. This might sound a bit tricky at first, but don't worry we'll break it down step by step, and soon you'll be a pro at understanding this unique aspect of the Roman numeral system.
In Roman numerals, we usually add symbols together to create numbers. For example, III means 3, and VI means 6. But there are some cases where subtraction comes into play, and that's what makes Roman numerals so interesting!
Let's start with the basics. Subtraction in Roman numerals is used in six specific cases: 4, 9, 40, 90, 400, and 900. These numbers are represented using a smaller numeral placed before a larger one, which tells us to subtract the smaller value from the larger one. It's like a little puzzle within the number system!
Let's look at each case in detail:
1. IV represents 4: Here, we're saying "one before five." So, it's 5 minus 1, which equals 4.
2. IX represents 9: This means "one before ten." We subtract 1 from 10 to get 9.
3. XL represents 40: Think of it as "ten before fifty." 50 minus 10 gives us 40.
4. XC represents 90: This is "ten before hundred," so 100 minus 10 equals 90.
5. CD represents 400: We're saying "hundred before five hundred," which is 500 minus 100, or 400.
6. CM represents 900: Finally, this means "hundred before thousand," so 1000 minus 100 gives us 900.
Now, you might be wondering, "Why use subtraction at all?" Well, it's all about efficiency and readability. Without subtraction, we'd have to write IIII for 4, which is longer and can be confusing. Using IV is shorter and clearer. The same goes for the other cases XC is much neater than LXXXX for 90!
Let's practice with a few examples. If you see XIV, you can break it down as X (10) + IV (4), which equals 14. For 39, we write XXXIX, which is XXX (30) + IX (9). See how it works?
There's an interesting exception to this subtraction rule, though. When we get to 4000, we don't use subtraction. Instead of writing something like MVM (5000 - 1000), we simply write MMMM. This is because the Romans didn't typically use numerals for numbers above 3999, but when they did, they stuck to addition.
Understanding subtraction in Roman numerals is like unlocking a secret code. It allows you to read and write numbers more efficiently in this ancient system. Remember, it's only used in those six specific cases we discussed, and each time, it's a smaller numeral before a larger one.
As you practice, you'll find that recognizing these subtraction patterns becomes second nature. It's a bit like learning a new language at first, you might need to think about each symbol, but soon you'll be reading Roman numerals fluently!
So, the next time you see a clock face with Roman numerals or a fancy building with a date inscribed in Roman numerals, you'll be able to decipher it with ease. You'll know that IV isn't just two random letters, but a clever way of writing 4. And when you see MCMXCIX, you'll quickly realize it's 1999 (1000 + (1000-100) + (100-10) + (10-1)).
Remember, the key to mastering subtraction in Roman numerals is practice and patience. Don't be discouraged if it takes a little time to get used to even the ancient Romans had to learn it! Keep exploring, keep practicing, and soon you'll be reading and writing
Practical Applications of Roman Numerals
Roman numerals, despite their ancient origins, continue to play a significant role in various aspects of modern life. From scientific notation to timekeeping, these classic symbols have found their way into numerous applications, proving that understanding Roman numerals is still relevant in today's world.
In the field of chemistry, Roman numerals are widely used to denote the oxidation state of elements in chemical formulas. For instance, iron(II) chloride is written as FeCl, where the Roman numeral II indicates that iron has an oxidation state of +2. This system helps chemists quickly identify the chemical properties of compounds.
Clock designs often incorporate Roman numerals for a touch of elegance and tradition. Many luxury watches and grandfather clocks feature Roman numerals on their faces, with XII at the top, VI at the bottom, and other numerals arranged accordingly. The use of Roman numerals in timepieces adds a classic aesthetic that appeals to many consumers.
When it comes to naming monarchs and popes, Roman numerals play a crucial role in distinguishing between individuals with the same name. For example, Queen Elizabeth II of the United Kingdom was easily differentiated from her predecessor, Queen Elizabeth I. Similarly, Pope Francis I is distinct from any future Pope Francis who may take the name. This system helps maintain clarity in historical records and official documents.
Legal documents often employ Roman numerals to organize sections and subsections. This practice enhances readability and allows for easy reference to specific parts of the document. For instance, you might see "Article IV, Section II" in a contract or constitution, providing a clear structure for complex legal texts.
Roman numerals are frequently used to mark dates on buildings, monuments, and tombstones. This tradition adds a sense of timelessness and grandeur to historical structures. The year 2023, for example, would be inscribed as MMXXIII. This practice not only preserves the aesthetic of classical architecture but also serves as a lasting record of important dates.
Understanding Roman numerals remains relevant in today's world for several reasons. Firstly, they are an integral part of our cultural heritage, connecting us to ancient civilizations and their mathematical achievements. Secondly, their continued use in various fields, from science to law, makes them a practical skill for many professionals. Lastly, Roman numerals add a touch of sophistication and classical elegance to design elements in both digital and physical spaces.
As students, appreciating the practical aspects of Roman numerals can enhance your understanding of history, improve your ability to interpret various texts and documents, and even give you an edge in fields like chemistry or law. Moreover, recognizing Roman numerals in everyday life from book chapters to movie credits can be a fun way to keep your mind sharp and engaged with this ancient yet enduring numbering system.
Converting Between Roman and Arabic Numerals
Converting between Roman and Arabic numerals is an essential skill that bridges ancient and modern number systems. This step-by-step guide will walk you through the process, providing clear instructions and examples for both Roman to Arabic and Arabic to Roman conversions.
Roman to Arabic Conversion
To convert Roman numerals to Arabic, follow these steps:
- Understand the basic Roman numeral symbols: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).
- Read the Roman numeral from left to right.
- Add the values of the symbols, unless a smaller value precedes a larger one.
- When a smaller value precedes a larger one, subtract the smaller from the larger.
Example: Converting XXVIII to Arabic
- X = 10
- X = 10
- V = 5
- I = 1
- I = 1
- I = 1
Total: 10 + 10 + 5 + 1 + 1 + 1 = 28
Arabic to Roman Conversion
To convert Arabic numerals to Roman, follow these steps:
- Break down the number into thousands, hundreds, tens, and ones.
- Convert each place value separately, starting with the largest.
- Use subtraction principle for numbers like 4 (IV), 9 (IX), 40 (XL), 90 (XC), 400 (CD), and 900 (CM).
Example: Converting 39 to Roman
- 30 = XXX
- 9 = IX
Result: XXXIX
Common Pitfalls and Tricks
- Remember that Roman numerals cannot have four identical symbols in a row.
- The subtraction principle only applies to powers of ten (I, X, C).
- Memorize common combinations like IV (4), IX (9), XL (40), XC (90).
- Practice with numbers ending in 4 and 9, as these often confuse beginners.
When converting from Arabic to Roman, it's helpful to start with the largest value and work your way down. For instance, to convert 2023:
- 2000 = MM
- 000 =
- 20 = XX
- 3 = III
Result: MMXXIII
For Roman to Arabic conversion, always read from left to right and remember the subtraction rule. If you encounter MCMXCIX, break it down:
- M = 1000
- CM = 900 (1000 - 100)
- XC = 90 (100 - 10)
- IX = 9 (10 - 1)
Total: 1000 + 900 + 90 + 9 = 1999
Practice is key to mastering these conversion techniques. Start with simple numbers and gradually increase complexity. Remember that Roman numerals typically don't exceed 3999 (MMM
Conclusion
In this exploration of Roman numerals, we've covered essential aspects including the symbols (I, V, X, L, C, D, M), addition rules (placing larger values before smaller ones), and subtraction principles (using smaller values before larger ones to indicate subtraction). We've seen how these ancient numerals still find applications in modern contexts, from clock faces to book chapters. The introductory video provided a crucial visual and auditory foundation, making the concept more accessible and engaging. As you continue your journey with Roman numerals, practice is key. Try converting dates, years, or even your favorite numbers to reinforce your understanding. Remember, grasping different number systems like Roman numerals not only enriches your mathematical knowledge but also connects you to centuries of human history and culture. This ancient system, still relevant today, demonstrates the enduring nature of mathematical concepts across time.
Introduction to Roman Numerals
Roman numerals are a numeral system that originated in ancient Rome and were used throughout the Roman Empire. Unlike the Arabic numerals (0-9) that we use today, Roman numerals are represented by combinations of letters from the Latin alphabet. This system is still in use in various applications in modern times.
Step 1: Understanding the Basics of Roman Numerals
Roman numerals are a way of writing numbers that originated in ancient Rome. Instead of using the digits 0-9, Roman numerals use combinations of letters from the Latin alphabet. The basic symbols used in Roman numerals are:
- I - 1
- V - 5
- X - 10
- L - 50
- C - 100
- D - 500
- M - 1000
These symbols can be combined in various ways to represent different numbers. For example, the number 2 is written as "II" (1+1), and the number 4 is written as "IV" (5-1).
Step 2: Comparison with Arabic Numerals
In modern mathematics, we primarily use Arabic numerals, which include the digits 0 through 9. This system is universal and is used worldwide for most mathematical and everyday purposes. However, the ancient Romans used their own system of numerals, which did not include a symbol for zero. This lack of a zero made the Roman numeral system less efficient for certain types of calculations, which is one reason why it was eventually replaced by the Arabic numeral system.
Step 3: The Roman Numeral System
The Roman numeral system is an additive and subtractive system. This means that numbers are formed by combining symbols and adding or subtracting their values. For example:
- III = 3 (1+1+1)
- IX = 9 (10-1)
- XX = 20 (10+10)
- XL = 40 (50-10)
- XC = 90 (100-10)
- CD = 400 (500-100)
- CM = 900 (1000-100)
By understanding these basic rules, you can read and write Roman numerals for any number.
Step 4: Modern Uses of Roman Numerals
Despite being an ancient system, Roman numerals are still used in various contexts today. Some common uses include:
- Chemistry: Roman numerals are used to denote the oxidation states of elements in chemical compounds, such as iron(II) oxide (FeO) and iron(III) oxide (Fe2O3).
- Clocks: Many traditional and decorative clocks use Roman numerals to mark the hours. For example, 12 is written as XII, 3 as III, and 6 as VI.
- Names: Monarchs and popes often have Roman numerals after their names to indicate their position in a sequence, such as King Edward VII or Pope John Paul II.
- Legal Documents: Roman numerals are used to number sections and subsections in legal documents and contracts, providing a clear and organized structure.
- Important Dates: Roman numerals are sometimes used to mark significant dates on buildings, monuments, and gravestones, adding a sense of historical importance.
Understanding Roman numerals can be useful in these contexts and can also provide a fun way to engage with history and classical studies.
Step 5: Practice and Application
To become proficient in reading and writing Roman numerals, practice is essential. Try converting various Arabic numbers to Roman numerals and vice versa. Additionally, pay attention to where you encounter Roman numerals in everyday life, such as on clocks, in books, or in movies. This will help reinforce your understanding and make the learning process more enjoyable.
FAQs
-
What are the basic symbols used in Roman numerals?
The basic symbols used in Roman numerals are:
- I = 1
- V = 5
- X = 10
- L = 50
- C = 100
- D = 500
- M = 1000
These symbols are combined to represent various numbers.
-
How does subtraction work in Roman numerals?
Subtraction in Roman numerals occurs when a smaller value is placed before a larger one. This is used in six specific cases:
- IV = 4 (5 - 1)
- IX = 9 (10 - 1)
- XL = 40 (50 - 10)
- XC = 90 (100 - 10)
- CD = 400 (500 - 100)
- CM = 900 (1000 - 100)
This method allows for more efficient representation of certain numbers.
-
Where are Roman numerals commonly used today?
Roman numerals are still used in various contexts, including:
- Clock faces and watch designs
- Numbering chapters in books
- Denoting the year of production in film credits
- Marking dates on buildings and monuments
- Naming successive monarchs and popes
- Indicating the oxidation state of elements in chemistry
-
How do you convert Arabic numerals to Roman numerals?
To convert Arabic numerals to Roman numerals:
- Break down the number into thousands, hundreds, tens, and ones.
- Convert each place value separately, starting with the largest.
- Use the subtraction principle for numbers like 4, 9, 40, 90, 400, and 900.
- Combine the resulting Roman numeral symbols.
For example, to convert 39 to Roman numerals: 30 = XXX, 9 = IX, so 39 = XXXIX.
-
What is the largest number that can be represented in standard Roman numerals?
The largest number typically represented in standard Roman numerals is 3999, which is written as MMMCMXCIX. This limitation exists because the Romans didn't have a symbol for 5000 or larger numbers. For numbers 4000 and above, they sometimes used a bar over a numeral to indicate multiplication by 1000, but this wasn't standardized. In modern usage, Roman numerals are generally not used for very large numbers, as the Arabic numeral system is more practical for such values.
Prerequisite Topics
Understanding the foundations of numerical systems is crucial when delving into the topic of "Representing numbers: Roman numerals." While there are no specific prerequisite topics listed for this subject, it's important to recognize that a solid grasp of basic mathematical concepts and number sense can greatly enhance your comprehension of Roman numerals.
Roman numerals represent a unique and historical method of expressing numbers, and their study can be both fascinating and enlightening. Although no formal prerequisites are required, having a strong foundation in basic arithmetic and an understanding of place value systems can significantly aid in grasping the principles behind Roman numerals.
Familiarity with our modern decimal system provides a valuable contrast when exploring Roman numerals. Understanding how we represent numbers using digits 0-9 and place value helps highlight the differences and similarities between these two numerical systems. This comparison can deepen your appreciation for the ingenuity of Roman numerals and their historical significance.
Additionally, a basic knowledge of ancient history, particularly Roman civilization, can provide context for why and how this number system developed. While not strictly necessary for understanding the mechanics of Roman numerals, this historical perspective can enrich your learning experience and make the topic more engaging.
As you embark on learning about Roman numerals, it's beneficial to approach the subject with curiosity and an open mind. The system may seem unusual at first, especially if you're accustomed to our modern decimal system. However, by drawing on your existing mathematical knowledge and problem-solving skills, you'll find that Roman numerals offer a unique perspective on number representation.
Remember that learning about Roman numerals isn't just about memorizing symbols and rules. It's an opportunity to explore different ways of thinking about numbers and to appreciate the evolution of mathematical notation. This study can enhance your overall numerical literacy and provide insights into how different cultures have approached the challenge of representing quantities.
While there may not be specific prerequisite topics listed, your general mathematical background and willingness to engage with new concepts will serve as a solid foundation for understanding Roman numerals. As you progress, you'll likely find connections between this ancient system and other areas of mathematics, further enriching your learning journey.
In conclusion, although no formal prerequisites are specified for studying Roman numerals, your existing mathematical knowledge and critical thinking skills will be valuable assets. Approach the topic with an open and inquisitive mindset, and you'll discover a fascinating aspect of numerical representation that has stood the test of time.

