Unequal probability outcomes

In this lesson, we will learn:

• In some probability scenarios, the outcomes are NOT all equally as likely to happen. Some outcomes will happen more often than others (have a greater chance of happening).
• How to write a probability fraction for events that have unequal outcomes

Notes:

• The outcomes for probability situation examples (coin toss, dice roll, equal parts spinner) have all had the same chance of happening. When all outcomes are just as likely (equally likely) to happen, there are even chances or equal chances of happening

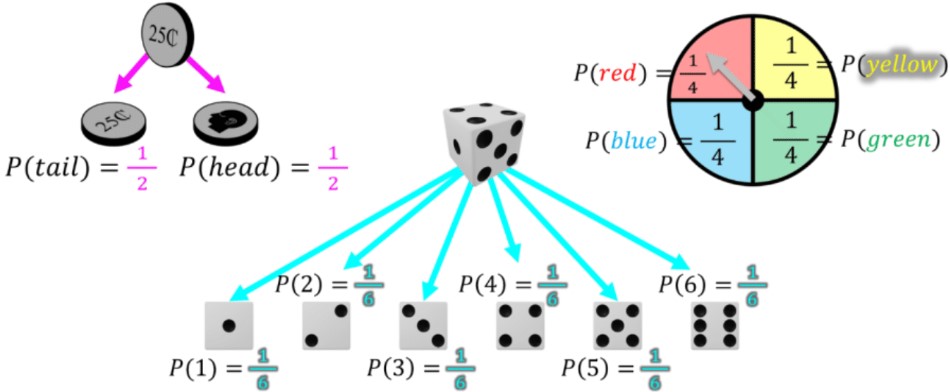
• When all outcomes are just as likely (equally likely) to happen, it is called having even chances
• Probabilities can be compared across different situations. The outcomes of the coin are more likely than the spinner, which are more likely than the outcomes of the die ($\frac{1}{2}$ > $\frac{1}{4}$ > $\frac{1}{6}$ )

• It is also possible for the outcomes to NOT be equally as likely; there are unequal chances of happening

Ex. unequal vs. equal outcomes for a spinner

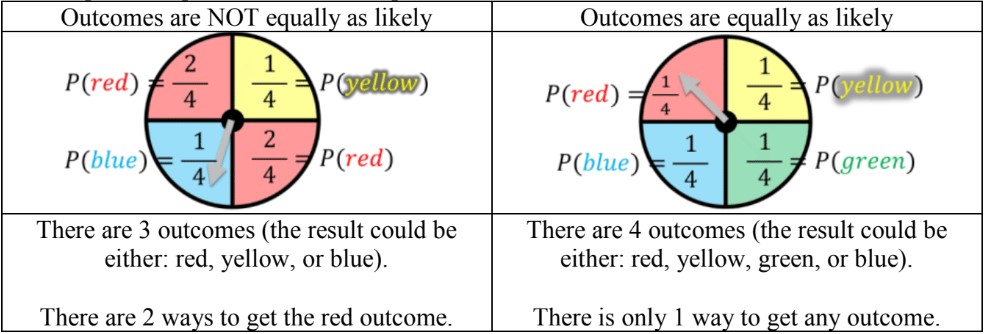
• The probability for situations with unequal outcomes can be given as a fraction in this formula format:

$P$(event) = $\frac{number\,ways\,to\,get\,the\,outcome}{number\,total\,ways\,of\,getting\,outcomes}$