Square measure
Topic Notes
In this lesson, we will learn:
- Square measure refers to the squared units that are used to measure area
- How to count the square measure of areas shown by unit square figures
- Comparing between metric units and squared metric units
Notes:
- Square measure refers to the units we use to measure area
- A unit square is a square with a measure of 1 unit on each side
- Units can be in metric units (i.e. m2, cm2, mm2) or other customary units (i.e. ft2, in2, yd2)
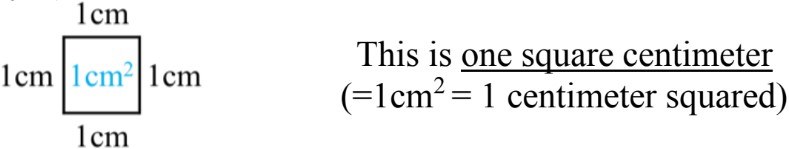
- Different dimensions (1-dimensional or 2-dimensional) correspond to geometric properties of shapes (perimeter or area) as well as their units:
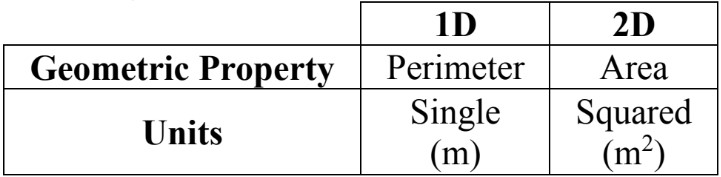
- The square measure of area can be thought of as the number of unit squares that cover the 2D shape. You can count each unit square one by one to find the area.
- If you have a rectangular figure of unit squares, think of it as an array:
- Converting between metric units: meters (m), centimeters (cm), millimeters (mm)

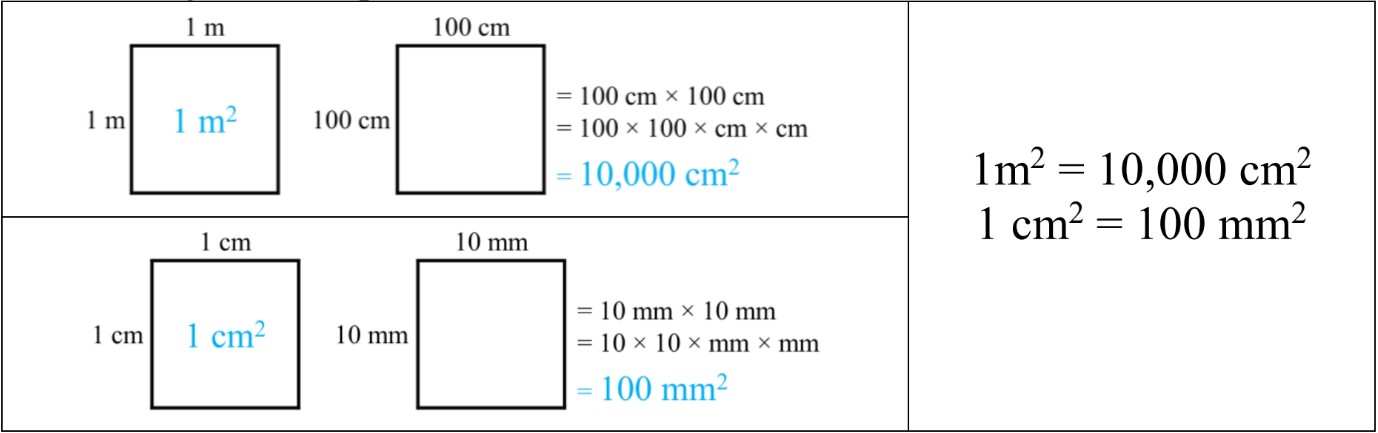
- Converting between squared metric units: m2, cm2, mm2
Introduction to Square Measure
Introduction to square measure is a fundamental concept in mathematics used for measuring the area of two-dimensional shapes. Our introduction to square measure video provides an essential overview of this important topic, helping students grasp the basics of square measure and its applications. By watching this video, learners will gain a clear understanding of how square measure is used to quantify the size of flat surfaces. Square measure is crucial in various fields, including architecture, landscaping, and engineering. It allows us to calculate the area of shapes like rectangles, squares, triangles, and circles. Understanding square measure is key to solving real-world problems involving area calculations. The video explains how different units of square measure, such as square meters, square feet, and square kilometers, are used depending on the scale of the object being measured. By mastering square measure, students will be better equipped to tackle more advanced geometric concepts and practical applications in their future studies and careers. The video explains how different units of square measure, such as square meters, square feet, and square kilometers, are used depending on the scale of the object being measured. By mastering square measure, students will be better equipped to tackle more advanced geometric concepts and practical applications in their future studies and careers.
Understanding Square Units
Square units are fundamental measurements used to quantify area, representing two-dimensional space. Unlike linear units, which measure length in one dimension, square units express the size of a surface or flat space. This distinction is crucial in various fields, including mathematics, physics, engineering, and everyday applications.
Linear units, such as meters (m) or centimeters (cm), measure distance in a straight line. In contrast, square units measure area, which is the product of two linear measurements. For instance, a square meter (m²) represents the area of a square that is one meter on each side. Similarly, a square centimeter (cm²) is the area of a square with sides measuring one centimeter each.
The notation for square units typically includes a superscript 2 after the linear unit symbol. This superscript indicates that the unit is squared or multiplied by itself. For example:
- cm² (square centimeters)
- m² (square meters)
- km² (square kilometers)
- in² (square inches)
- ft² (square feet)
This superscript notation is essential for distinguishing between linear and square measurements. Without it, there could be confusion about whether a measurement refers to length or area.
To better understand the relationship between linear and square units, consider the following example:
Imagine a square room with sides measuring 5 meters. The perimeter of this room, which is a linear measurement, would be 20 meters (5m + 5m + 5m + 5m). However, the area of the room, expressed in square units, would be 25 square meters (5m × 5m = 25m²). This example illustrates how linear units (meters) are used to measure the room's edges, while square units (square meters) quantify the floor space.
The conversion between different square units follows a squared relationship. For instance, to convert square centimeters to square meters:
1 m² = 100 cm × 100 cm = 10,000 cm²
This relationship demonstrates why working with converting square units often involves larger numbers compared to linear units.
Square units find applications in numerous real-world scenarios:
- Real estate: Measuring property sizes and living spaces
- Construction: Calculating material requirements for flooring, roofing, or painting
- Agriculture: Assessing crop yields and land usage
- Environmental science: Quantifying forest coverage or habitat areas
- Physics: Describing pressure (force per unit area)
Understanding the difference between linear and square units is crucial for accurate measurements and calculations. While linear units provide information about length or distance, square units offer insights into the size of surfaces or areas. This distinction becomes even more significant when dealing with three-dimensional measurements, where cubic units (e.g., m³) come into play.
In conclusion, square units, denoted by the superscript 2, are essential for measuring and expressing area in various fields. They differ fundamentally from linear units by representing two-dimensional space rather than just length. Recognizing this difference and using the appropriate unit of measurement ensures accuracy in calculations and effective communication of spatial information across diverse applications.
For more information on converting square units, you can refer to additional resources.
Converting Between Square Units
Converting between different square units is a fundamental skill in mathematics and various practical applications. This process involves understanding the relationship between different units of area measurement and applying the correct conversion factors. One crucial aspect to remember is that conversion factors for square units are squared compared to their linear counterparts.
Let's start with the basics of square unit conversion. The most common conversions involve moving between square meters (m²), square centimeters (cm²), and square millimeters (mm²). To convert from a larger unit to a smaller unit, we multiply by the square of the conversion factor. Conversely, when converting from a smaller unit to a larger unit, we divide by the square of the conversion factor.
For example, to convert from m² to cm², we multiply by 10,000. This is because 1 meter equals 100 centimeters, and when we square this relationship for area, we get 100 × 100 = 10,000. Similarly, to convert from cm² to mm², we multiply by 100, as 1 centimeter equals 10 millimeters, and 10 × 10 = 100.
Let's walk through a step-by-step example of converting 5 m² to cm²:
- Identify the conversion factor: 1 m² = 10,000 cm²
- Set up the conversion: 5 m² × (10,000 cm² / 1 m²)
- Cancel out the units: The m² cancels out, leaving cm²
- Perform the calculation: 5 × 10,000 = 50,000 cm²
Now, let's convert 7,500 cm² to mm²:
- Identify the conversion factor: 1 cm² = 100 mm²
- Set up the conversion: 7,500 cm² × (100 mm² / 1 cm²)
- Cancel out the units: The cm² cancels out, leaving mm²
- Perform the calculation: 7,500 × 100 = 750,000 mm²
It's important to note that students often make common mistakes when converting square units. One frequent error is using the linear conversion factor instead of squaring it. For instance, a student might incorrectly multiply by 100 instead of 10,000 when converting from m² to cm². Another common mistake is forgetting to square the conversion factor altogether, leading to incorrect results.
To avoid these errors, always remember that area is two-dimensional, so conversion factors must be squared. It can be helpful to visualize the conversion as a square with sides equal to the linear conversion factor. For example, when converting from m² to cm², imagine a square meter divided into 100 rows and 100 columns of square centimeters.
Another tip for accurate conversions is to write out the units at each step and ensure they cancel out correctly. This practice helps catch errors and reinforces the understanding of the conversion process. Additionally, estimating the result before calculating can serve as a sanity check. For instance, when converting from a larger unit to a smaller unit, the numerical value should increase, and vice versa.
It's also beneficial to memorize some common conversion factors, such as 1 m² = 10,000 cm² and 1 cm² = 100 mm². Having these at your fingertips can speed up calculations and help verify more complex conversions. For less common conversions, remember that you can always break them down into steps using these familiar relationships.
In conclusion, mastering square unit conversion is essential for many fields, including engineering, architecture, and physics. By understanding the principle of squaring conversion factors, following a step-by-step approach, and being aware of common pitfalls, you can confidently and accurately convert between different square units. Practice regularly with various examples to reinforce your skills and develop an intuitive sense for these conversions.
Applications of Square Measure
Square measure, a fundamental concept in geometry, finds numerous practical applications in our daily lives and various professional fields. This unit of measurement is essential for quantifying two-dimensional spaces and surfaces, making it indispensable in both everyday scenarios and specialized industries.
In everyday life, one of the most common applications of square measure is in measuring floor area. Whether you're moving into a new home, rearranging furniture, or shopping for carpets, understanding the square footage of a room is crucial. Homeowners and renters alike use square measure to determine the size of living spaces, bedrooms, and kitchens, helping them make informed decisions about furniture placement and overall space utilization.
Another practical use of square measure is in calculating the amount of paint needed for walls. DIY enthusiasts and professional painters rely on accurate measurements of wall areas to estimate the quantity of paint required for a project. By multiplying the length and height of each wall and summing up the total square footage, one can determine how many gallons or liters of paint to purchase, avoiding waste or shortages.
Gardening enthusiasts and landscapers frequently employ square measure when planning and maintaining outdoor spaces. Whether designing a vegetable garden, flower bed, or lawn area, understanding the square footage helps in determining the number of plants needed, the amount of soil or mulch required, and even calculating irrigation needs. This knowledge enables efficient use of resources and optimal plant spacing for healthy growth.
In the professional realm, architects heavily rely on square measure in their designs and blueprints. They use it to calculate the total floor area of buildings, ensure compliance with zoning regulations, and optimize space utilization. Architects must consider factors such as room sizes, hallway widths, and overall building footprints, all of which are expressed in square measure.
Surveyors, another group of professionals, use square measure extensively in their work. They measure and map land areas for various purposes, including property boundaries, construction projects, and environmental assessments. Accurate square measure calculations are crucial for legal documentation, land valuation, and urban planning.
In the construction industry, contractors and builders use square measure to estimate material quantities. From flooring and roofing to drywall and insulation, precise area measurements ensure accurate ordering of materials, reducing waste and controlling costs. This application extends to estimating labor costs, as many construction tasks are priced based on the square footage involved.
Real estate professionals rely heavily on square measure when listing and valuing properties. The total square footage of a home or commercial building is a key factor in determining its market value and rental rates. Accurate measurements are essential for fair comparisons between properties and ensuring transparency in real estate transactions.
In the realm of energy efficiency, square measure plays a crucial role in calculating heating and cooling requirements for buildings. HVAC specialists use floor area measurements to determine the appropriate size and capacity of heating and air conditioning systems, ensuring optimal comfort and energy usage.
Even in retail and commercial spaces, square measure is vital for space planning and inventory management. Store layouts, shelf space allocation, and warehouse organization all depend on accurate area measurements to maximize efficiency and profitability.
In conclusion, square measure applications permeate numerous aspects of our lives and various professional fields. From the simple task of measuring a room for new furniture to complex architectural designs and land surveys, this fundamental unit of measurement proves invaluable. Its versatility and practicality make it an essential tool for anyone involved in spatial planning, construction, or property management. Understanding and effectively using square measure can lead to more efficient use of space, better resource management, and improved decision-making in both personal and professional contexts.
Common Shapes and Their Square Measures
Calculating the square measure, or area, of common shapes is a fundamental skill in geometry and practical applications. This guide will walk you through the process of determining the area of squares, rectangles, triangle area calculation, and circles, providing formulas and example problems for each shape.
Square Area Calculation
The area of a square is the simplest to calculate. The formula is:
Area = side length × side length or A = s²
Example: If a square has a side length of 5 meters, its area would be 5 × 5 = 25 square meters.
Rectangle Area Calculation
For rectangles, we use the formula:
Area = length × width or A = l × w
Example: A rectangle with a length of 8 feet and a width of 3 feet has an area of 8 × 3 = 24 square feet.
Triangle Area Calculation
The area of a triangle is calculated using the formula:
Area = ½ × base × height or A = ½bh
Example: A triangle with a base of 6 inches and a height of 4 inches has an area of ½ × 6 × 4 = 12 square inches.
Circle Area Calculation
Circles require the use of pi (π) in their area formula:
Area = π × radius² or A = πr²
Example: A circle with a radius of 2 centimeters has an area of π × 2² = 12.57 square centimeters (rounded to two decimal places).
Importance of Consistent Units
When calculating area, it's crucial to use consistent units throughout your measurements and calculations. Mixing units can lead to incorrect results. For instance, if you're working with a rectangle where the length is in feet and the width is in inches, you must convert one measurement to match the other before calculating the area.
Example of unit consistency: A rectangle with a length of 2 meters and a width of 50 centimeters.
Incorrect: 2 × 50 = 100 (This result is meaningless as it mixes units)
Correct: Convert 50 cm to 0.5 m, then calculate: 2 × 0.5 = 1 square meter
Practice Problems
1. Calculate the area of a square with a side length of 7 yards.
2. Find the area of a rectangle with a length of 12 feet and a width of 5 feet.
3. Determine the area of a triangle with a base of 10 meters and a height of 6 meters.
4. What is the area of a circle with a radius of 3 inches?
Conclusion
Understanding how to calculate the area of common shapes is essential for various real-world applications, from carpentry and landscaping to architecture and engineering. By mastering these formulas and practicing with different scenarios, you'll develop a strong foundation in area calculation. Remember to always double-check your units and use consistent measurements to ensure accurate results in your area calculations.
Square Measure in the Metric and Imperial Systems
When it comes to measuring area, two primary systems dominate: the metric system and the imperial system. Each has its own set of units for square measure, and understanding the differences and conversions between them is crucial for various applications. The metric system, used widely around the world, offers a more straightforward decimal-based approach, while the imperial system, still prevalent in countries like the United States, has its roots in historical measurements.
In the metric system, square measure units are based on powers of 10. The most common units include square centimeters (cm²), square meters (m²), and square kilometers (km²). These units are logically related, with 1 m² equal to 10,000 cm² and 1 km² equal to 1,000,000 m². This consistency makes calculations and conversions within the metric system relatively simple.
The imperial system, on the other hand, uses units such as square inches, square feet, square yards, and square miles. The relationships between these units are less intuitive, with 1 square foot equal to 144 square inches, 1 square yard equal to 9 square feet, and 1 square mile equal to 27,878,400 square feet. This complexity can make conversions within the imperial system more challenging.
The choice between metric and imperial units often depends on the context and location. The metric system is the standard for scientific and international communication, as well as in most countries worldwide. The imperial system is primarily used in the United States for everyday measurements and in certain industries. However, even in the U.S., the metric system is widely used in scientific and medical fields.
For those working across both systems, knowing conversion factors is essential. Here are some common conversions:
- 1 square inch 6.4516 cm²
- 1 square foot 0.0929 m²
- 1 square yard 0.8361 m²
- 1 square mile 2.59 km²
- 1 cm² 0.1550 square inches
- 1 m² 10.7639 square feet
- 1 km² 0.3861 square miles
Understanding these conversions is particularly important in fields like construction, real estate, and international trade, where measurements may need to be translated between systems. For example, a European architect designing a building for an American client would need to convert metric to imperial area conversion for local contractors.
In conclusion, while the metric system offers simplicity and is widely adopted globally, the imperial system remains relevant in certain regions and industries. Proficiency in both systems and the ability to convert between them ensures effective communication and accuracy in various professional and personal contexts involving area measurements. For instance, knowing the metric to imperial area conversion can be crucial in many practical scenarios.
Conclusion
In summary, square measure is a fundamental concept in geometry and real-world applications. Understanding square units is crucial for accurately measuring and comparing areas of various shapes and sizes. From calculating floor space in homes to determining land area for agriculture, square measure plays a vital role in numerous fields. To reinforce your understanding, practice converting between different square units, such as square meters to square feet, and calculate areas of diverse shapes like rectangles, triangles, and circles. Remember, mastering these skills will enhance your ability to solve practical problems in construction, landscaping, and urban planning. Don't hesitate to revisit the introduction video for a visual explanation of these concepts. By honing your square measure skills, you'll be better equipped to tackle real-world challenges and make informed decisions in various professional and personal contexts. Keep practicing and applying these concepts to solidify your understanding of square measure.
Introduction to Square Measure: What is square measure?
Square measure is a fundamental concept in geometry and measurement, used to determine the area of two-dimensional shapes. This guide will walk you through the key aspects of square measure, explaining its components and how it is used in practical scenarios.
Step 1: Understanding the Term "Square Measure"
The term "square measure" can be broken down into two parts: "square" and "measure." The word "square" refers to the 2D shape of a square, which is a four-sided polygon with all sides of equal length. The "measure" part refers to the units used to quantify the dimensions of the square. When combined, "square measure" pertains to the measurement of area using square units.
Step 2: Units of Measurement
When measuring area, we use specific units. Common metric units include centimeters (cm), meters (m), and millimeters (mm). In the customary system, units such as feet (ft), inches (in), and yards (yd) are used. The key feature of square measure is the use of these units with an exponent of 2, indicating that we are measuring area. For example, cm² (square centimeters) or m² (square meters).
Step 3: The Concept of Square Units
Square units are used to measure area. For instance, a square with each side measuring 1 cm is called a unit square. The area of this unit square is 1 cm². When we measure larger areas, we count how many of these unit squares fit within the shape. This is why we use the exponent of 2, as it signifies that we are dealing with two dimensions: length and width.
Step 4: Calculating Area
To calculate the area of a shape, we multiply its length by its width. For example, if a square has sides of 1 cm each, its area is 1 cm × 1 cm = 1 cm². This multiplication of dimensions is why we see the exponent of 2 in square units. The same principle applies to other shapes; for a rectangle, the area is found by multiplying its length by its width.
Step 5: Practical Application of Square Measure
Square measure is used in various real-world applications, such as determining the area of a room for flooring, calculating the size of a plot of land, or measuring the surface area of objects. By understanding square measure, we can accurately quantify and compare different areas, making it an essential skill in both everyday life and professional fields like architecture and engineering.
Step 6: Distinguishing Between Perimeter and Area
It's important to differentiate between perimeter and area. Perimeter is the total distance around the edges of a shape, measured in linear units (e.g., cm, m). Area, on the other hand, is the space covered by the shape, measured in square units (e.g., cm², m²). Understanding this distinction helps in applying the correct measurement techniques for different scenarios.
Step 7: Visualizing Square Measure
Visual aids can help in understanding square measure. Imagine a grid of unit squares covering a shape. By counting these squares, we can determine the area. For example, a rectangle with a length of 3 cm and a width of 2 cm would be covered by 6 unit squares, giving it an area of 6 cm². This visualization reinforces the concept of multiplying dimensions to find area.
Step 8: Summary and Review
In summary, square measure is a method of quantifying the area of 2D shapes using square units. It involves understanding the components of the term, using appropriate measurement units, calculating area through multiplication of dimensions, and applying this knowledge in practical situations. By mastering square measure, you can accurately measure and compare areas, enhancing your understanding of geometry and its applications.
FAQs
-
What is square measure?
Square measure is a unit of area measurement used to quantify two-dimensional spaces. It represents the size of a surface or flat space and is typically expressed in units such as square meters (m²), square feet (ft²), or square kilometers (km²).
-
How do you convert between different square units?
To convert between square units, you need to square the conversion factor used for linear measurements. For example, to convert from square meters to square centimeters, multiply by 10,000 (100 x 100) since 1 meter = 100 centimeters. Always remember to square the conversion factor for area conversions.
-
What are some common applications of square measure?
Square measure is used in various fields, including real estate (measuring property sizes), construction (calculating material requirements), agriculture (assessing land usage), and urban planning. It's also essential for everyday tasks like determining paint needed for walls or carpet for flooring.
-
How do you calculate the area of a circle?
The area of a circle is calculated using the formula A = πr², where A is the area, π (pi) is approximately 3.14159, and r is the radius of the circle. For example, a circle with a radius of 5 meters would have an area of approximately 78.54 square meters.
-
What's the difference between metric and imperial square measures?
Metric square measures (e.g., square meters, square kilometers) are based on powers of 10, making conversions simpler. Imperial square measures (e.g., square feet, square yards) have less intuitive relationships. For instance, 1 square yard = 9 square feet. The metric system is more widely used globally, while the imperial system is common in countries like the United States.
Prerequisite Topics
Understanding square measure is crucial in various fields, from mathematics to real-world applications. However, to fully grasp this concept, it's essential to have a solid foundation in certain prerequisite topics. One of the most important prerequisites is conversions involving squares and cubic measurements. This fundamental skill is vital for accurately working with square measures and understanding their relationships to other units of measurement.
When delving into square measure, you'll often encounter situations where you need to convert between different units of area. This is where your knowledge of conversions becomes invaluable. For instance, you might need to convert square feet to square meters or vice versa. Without a strong grasp of conversion techniques, you may struggle to perform these calculations accurately, potentially leading to errors in your work or misunderstandings of spatial relationships.
Moreover, understanding conversions is particularly important when dealing with the imperial system area units, which are still widely used in some countries. The imperial system can be more challenging to work with due to its non-decimal nature, making conversions even more critical. By mastering these conversions, you'll be better equipped to handle a variety of square measure problems, regardless of the unit system being used.
Another aspect where conversions play a crucial role is in understanding the relationship between linear measurements and square measures. For example, knowing how to convert between inches and square inches, or feet and square feet, is essential for calculating areas accurately. This skill is not only useful in academic settings but also in practical applications such as construction, interior design, and land surveying.
Furthermore, the ability to work with conversions involving squares and cubic measurements extends beyond just square measures. It lays the groundwork for understanding more complex concepts like volume and surface area. These topics are closely related to square measure and often build upon the same foundational knowledge.
In conclusion, mastering the prerequisite topic of conversions involving squares and cubic measurements is essential for a comprehensive understanding of square measure. It provides you with the tools to work confidently with different units of area, navigate between various measurement systems, and solve real-world problems involving square measures. By investing time in strengthening your knowledge of these conversions, you'll be setting yourself up for success in more advanced mathematical concepts and practical applications related to area and spatial relationships.

