Fractions of a set
Topic Notes
In this lesson, we will learn:
- How to use fractions to talk about sets of objects
- How to use division and multiplication to solve for fraction of a set
Notes:
- We can use fractions to talk about sets of objects. We can use images or just simplify to a simple shape like a circle.
- Ex. If Austin has 8 jellybeans and he wants to give to her, how many jellybeans will he give?
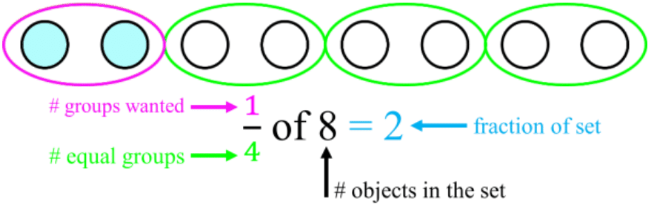
- By making 4 equal groups and then giving just 1 of those groups, we realize that there is 2 in each group, so he gave his sister 2 jellybeans.
- We can use division and multiplication to find the fraction of a set
- Ex. After giving his sister jellybeans, Austin has of his 8 jellybeans left.
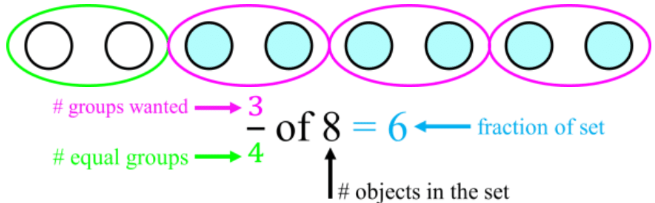
- Step 1: divide 8 into 4 equal groups 8 ÷ 4 = 2
- Step 2: take the result and multiply by 3 groups 2 × 3 = 6
- The formula for a fraction of a set:
- following the format:
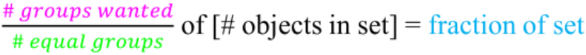
- divide the denominator and multiply the numerator
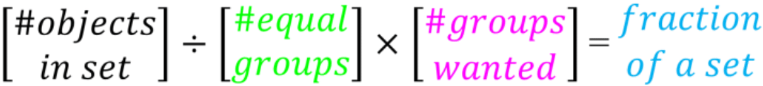
Introduction to Fractions of a Set
Welcome to our lesson on fractions of a set! This fundamental concept is crucial for understanding more advanced mathematical topics. To kick things off, we've prepared an introduction video that will give you a clear visual representation of how fractions work within sets. This video is an essential starting point, as it breaks down the concept into easy-to-grasp examples. You'll see how we can divide a group of objects into equal parts and express those parts as fractions. For instance, if we have 12 apples and want to represent 1/3 of them, we're looking at 4 apples. As we progress, you'll learn how to calculate various fractions of different set sizes, apply this knowledge to real-world scenarios, and solve more complex problems. Remember, mastering fractions of a set is a stepping stone to more advanced math concepts, so let's dive in and make sure you have a solid foundation!
Understanding Fractions of a Set
Have you ever wondered how to divide a group of objects into equal parts? That's where fractions of a set come in handy! Let's explore this concept using everyone's favorite candy: jelly beans!
Imagine you have a colorful jar of jelly beans. These jelly beans represent our "set" - the whole group we're working with. Now, let's learn how to split this set into fractions.
What are Fractions of a Set?
Fractions of a set refer to dividing a group of objects into equal parts. It's like sharing your jelly beans with friends, making sure everyone gets the same amount. Each part represents a fraction of the whole set.
Step-by-Step Guide to Understanding Fractions of a Set
- Count your set: First, count how many jelly beans you have in total. Let's say you have 12 jelly beans.
- Decide on your fraction: Choose the fraction you want to work with. For example, let's find 1/3 of the set.
- Divide into equal groups: To find 1/3, we need to split our jelly beans into 3 equal groups. 12 ÷ 3 = 4, so each group will have 4 jelly beans.
- Identify the fraction: One group of 4 jelly beans represents 1/3 of the entire set.
Visual Representation
Picture this: | |
Each color represents a group of 4 jelly beans. One group (like the red ones) is 1/3 of the set.
More Examples
Let's try another example. Say you have 20 jelly beans and want to find 1/4 of the set:
- Count your set: 20 jelly beans
- Decide on your fraction: 1/4
- Divide into equal groups: 20 ÷ 4 = 5
- Identify the fraction: One group of 5 jelly beans is 1/4 of the set
Why is This Important?
Understanding fractions of a set helps in many real-life situations. It's useful for:
- Sharing food or toys equally
- Dividing tasks among team members
- Understanding parts of a whole in math and science
Practice Makes Perfect
To get better at working with fractions of a set, try these fun activities:
- Use different objects like marbles, buttons, or even pieces of fruit
- Try finding different fractions of various set sizes
- Create visual representations using drawings or actual objects
Remember
When working with fractions of a set:
- The denominator (bottom number) of the fraction tells you how many equal groups to make
- The numerator (top number) tells you how many of those groups to consider
- Always start by counting your total set
Fractions of a set might seem tricky at first, but with practice, you'll be dividing groups like a pro! Whether you're sharing jelly beans with friends or solving math problems, this skill will come in handy
Visualizing Fractions of a Set
The simplified circle model is an excellent tool for representing fractions of a set, making it easier to understand and visualize these mathematical concepts. This model provides a clear and intuitive way to interpret the numerator and denominator, helping students and learners grasp fraction-related problems more effectively.
In the circle model, we start with a complete circle representing the whole set. This circle is then divided into equal parts, with the number of parts corresponding to the denominator of the fraction. The denominator tells us how many equal parts the whole set is divided into. For example, if we have a fraction with a denominator of 4, we would divide our circle into four equal parts.
The numerator in this model represents the number of parts we are considering or focusing on. It tells us how many of the equal parts we should highlight or count. For instance, if we have a fraction of 3/4, we would shade or highlight three out of the four equal parts in our circle.
This visual representation makes it much easier to understand what a fraction actually means in the context of a set. It clearly shows the relationship between the part (numerator) and the whole (denominator), allowing for a more intuitive grasp of the concept.
Let's look at some examples of how to use this model to solve problems:
1. Comparing fractions: If we want to compare 1/3 and 1/4, we can draw two circles. The first circle would be divided into three equal parts with one part shaded, while the second would be divided into four equal parts with one part shaded. It becomes visually apparent that 1/3 is larger than 1/4.
2. Adding fractions: To add 1/4 and 2/4, we can use a single circle divided into four parts. We would shade one part for 1/4 and then shade two more parts for 2/4. The result is clearly 3/4, as three out of the four parts are now shaded.
3. Finding equivalent fractions: If we want to show that 1/2 is equivalent to 2/4, we can draw two circles. One circle would be divided in half with one part shaded, while the other would be divided into four parts with two parts shaded. The visual similarity makes the equivalence clear.
4. Solving word problems: If a recipe calls for 3/4 cup of flour and we want to know how much is needed for half the recipe, we can draw a circle divided into four parts with three shaded. Then, we can visually halve this, resulting in a circle with two parts out of four shaded, clearly showing 2/4 or 1/2 cup is needed.
The circle model is particularly useful for teaching fractions to visual learners. It provides a concrete representation of abstract concepts, making it easier for students to understand and remember fraction relationships. Teachers and parents can use this model to explain fraction concepts, from basic comparisons to more complex operations like addition and subtraction of fractions.
As learners become more comfortable with the circle model, they can start to mentally visualize these representations, enhancing their ability to work with fractions quickly and accurately. This skill is invaluable in many real-world applications, from cooking and construction to more advanced mathematical and scientific concepts.
In conclusion, the simplified circle model is a powerful tool for representing fractions of a set. By clearly illustrating the relationship between the numerator and denominator, it provides a visual and intuitive understanding of fractions. Whether you're a student learning fractions for the first time or an educator looking for effective teaching methods, the circle model offers a friendly and accessible approach to mastering this fundamental mathematical concept.
Mathematical Shortcuts for Unit Fractions
When it comes to solving fractions of a set problems, there's a nifty mathematical shortcut that can save you time and effort, especially when dealing with unit fractions. A unit fraction is a fraction where the numerator is 1, such as 1/2, 1/3, or 1/7. This shortcut involves using division instead of the traditional multiplication method, and it's both elegant and efficient.
Here's the key insight: when you're finding a unit fraction of a set, you can simply divide the total number in the set by the denominator of the unit fraction. For example, if you want to find 1/4 of 20, instead of multiplying 20 by 1/4, you can just divide 20 by 4. This gives you the same result (5) but with less computational effort.
Why does this work? The mathematical reasoning behind this shortcut is quite straightforward. When we take a fraction of a number, we're essentially dividing that number into equal parts and then taking a certain number of those parts. With a unit fraction, we're always taking just one of those parts. So, if we divide the total by the denominator, we're directly calculating the size of one of those equal parts.
Let's look at a few more examples to solidify this concept:
1. To find 1/3 of 18: Instead of 18 × 1/3, simply do 18 ÷ 3 = 6
2. For 1/5 of 30: Rather than 30 × 1/5, calculate 30 ÷ 5 = 6
3. To determine 1/8 of 64: Instead of 64 × 1/8, just do 64 ÷ 8 = 8
This shortcut is particularly useful in mental math situations or when you're trying to quickly estimate results. It's important to note that this method only works for unit fractions. For non-unit fractions (where the numerator is not 1), you'll need to use a different approach.
As a math tutor, I always encourage students to understand why shortcuts work rather than just memorizing them. This particular shortcut is a great example of how understanding the underlying concept (in this case, the relationship between fractions and division) can lead to more efficient problem-solving techniques. By mastering this shortcut, you'll be able to tackle fraction-of-a-set problems involving unit fractions with greater speed and confidence.
Solving Non-Unit Fractions of a Set
When it comes to solving problems involving non-unit fractions of a set, many students find themselves scratching their heads. But fear not! With a simple two-step process, you'll be tackling these problems like a pro in no time. Let's dive into the world of non-unit fractions and discover how to solve them efficiently.
First, let's clarify what we mean by a non-unit fraction. Unlike unit fractions, which always have a numerator of 1 (like 1/2 or 1/3), non-unit fractions can have any number as the numerator (such as 2/3 or 3/4). When we're dealing with a fraction of a set, we're essentially looking to find a part of a whole group of items.
The key to solving problems with non-unit fractions of a set lies in a simple two-step process: divide by the denominator, then multiply by the numerator. This method works consistently and can be applied to any non-unit fraction problem. Let's break it down:
Step 1: Divide the total number in the set by the denominator of the fraction. This step helps us determine the size of one part of the fraction.
Step 2: Multiply the result from step 1 by the numerator of the fraction. This gives us the final answer, representing the number of items in the fraction of the set we're looking for.
Let's illustrate this with an example. Suppose we have a set of 24 marbles, and we want to find 3/4 of this set. Here's how we'd solve it:
1. Divide 24 (total marbles) by 4 (denominator): 24 ÷ 4 = 6
2. Multiply the result (6) by 3 (numerator): 6 × 3 = 18
Therefore, 3/4 of 24 marbles is 18 marbles.
But why does this method work? The magic lies in the nature of fractions themselves. When we divide by the denominator, we're essentially breaking the set into equal parts based on the fraction's bottom number. This gives us the size of one part. Then, by multiplying by the numerator, we're taking that many parts of the whole, which gives us our final answer.
This method is versatile and can be applied to various real-world scenarios. For instance, if you need to calculate 2/5 of your monthly salary for savings, or 3/8 of a recipe's ingredients when scaling it down, you'd use the same approach.
Let's try another example to reinforce the concept. Say we want to find 5/6 of 30 students:
1. Divide 30 (total students) by 6 (denominator): 30 ÷ 6 = 5
2. Multiply the result (5) by 5 (numerator): 5 × 5 = 25
So, 5/6 of 30 students is 25 students.
As you practice this method, you'll find that it becomes second nature. The key is to remember the order: divide first, then multiply. This approach works because it maintains the proportional relationship expressed by the fraction while applying it to the specific quantity in your set.
In conclusion, solving problems involving non-unit fractions of a set doesn't have to be daunting. By following the simple two-step process of dividing by the denominator and multiplying by the numerator, you can confidently tackle any such problem that comes your way. Remember, practice makes perfect, so don't hesitate to work through various examples to solidify your understanding. Before you know it, you'll be a non-unit fraction master!
Practice Problems and Applications
Let's dive into some exciting practice problems involving fractions of a set! We'll start with simpler examples and gradually move to more complex ones. Don't worry if you find some challenging at first with practice, you'll become a fraction master in no time!
1. Basic Fraction of a Set
Problem: In a classroom of 24 students, 1/3 of them are wearing red shirts. How many students are wearing red shirts?
Solution:
- Identify the total number of students: 24
- Identify the fraction: 1/3
- Calculate: 24 ÷ 3 = 8
Therefore, 8 students are wearing red shirts.
2. Multiple Fractions of a Set
Problem: In a fruit basket with 30 pieces of fruit, 1/2 are apples, 1/3 are oranges, and the rest are bananas. How many of each fruit are there?
Solution:
- Calculate apples: 30 × 1/2 = 15 apples
- Calculate oranges: 30 × 1/3 = 10 oranges
- Calculate bananas: 30 - 15 - 10 = 5 bananas
3. Real-World Application: Recipe Scaling
Problem: A recipe for 8 servings calls for 2/3 cup of sugar. How much sugar is needed for 12 servings?
Solution:
- Find sugar per serving: 2/3 ÷ 8 = 1/12 cup per serving
- Calculate for 12 servings: 1/12 × 12 = 1 cup of sugar
4. Complex Fraction of a Set
Problem: In a school of 450 students, 2/5 play sports. Of those who play sports, 3/4 play team sports. How many students play individual sports?
Solution:
- Calculate students who play sports: 450 × 2/5 = 180
- Calculate students who play team sports: 180 × 3/4 = 135
- Calculate individual sports players: 180 - 135 = 45
5. Real-World Application: Financial Planning
Problem: Sarah saves 1/4 of her monthly salary. If she saves $300 per month, what is her monthly salary?
Solution:
- Set up the equation: 1/4 × Monthly Salary = $300
- Multiply both sides by 4: Monthly Salary = $300 × 4
- Calculate: Monthly Salary = $1,200
Great job working through these problems! Remember, fractions of a set are incredibly useful in everyday life. Whether you're cooking, managing finances, or analyzing data, this skill will come in handy. Keep practicing, and don't hesitate to apply these concepts to real-world situations you encounter.
Tips for Success:
- Always identify the total set and the fraction clearly.
- Break down complex problems into smaller steps.
- Double-check your calculations.
- Look for real-life situations where you can apply these skills.
As you
Common Mistakes and How to Avoid Them
When working with fractions of a set, students often encounter challenges that can lead to errors. Understanding these common mistakes and learning strategies to avoid them is crucial for mastering this important mathematical concept. Let's explore some of the most frequent pitfalls and how to overcome them.
One of the most common mistakes is misinterpreting the whole set. For example, if asked to find 3/4 of 20 marbles, some students might incorrectly assume that 3/4 represents 15 marbles (3 + 4 = 7, and 20 - 7 = 13). To avoid this error, always remember that the denominator represents the total parts of the whole, not a number to be subtracted.
Another frequent error is forgetting to divide the total set into equal parts. When finding 2/5 of 30 students, it's crucial to first divide 30 by 5 to determine the size of each part (6 students). Only then can you multiply by 2 to get the correct answer of 12 students. A helpful strategy is to always start by dividing the total by the denominator before proceeding.
Students often struggle with mixed numbers in sets. For instance, when calculating 2 1/3 of 18 apples, some might only consider the whole number 2 and ignore the fraction. To avoid this, convert mixed numbers to improper fractions first (2 1/3 = 7/3) before performing calculations.
Confusion can arise when dealing with proper fractions greater than one-half. For example, finding 5/8 of 40 books might lead some students to think it's less than half, when it's actually more. Always compare the fraction to 1/2 as a quick mental check before calculating.
A helpful strategy to prevent errors is to estimate the answer before calculating. If you're finding 3/4 of 100 items, you know the answer should be more than half but less than the whole amount, so an answer around 75 makes sense.
Lastly, many students forget to label their final answer or provide context. Always remember to include units or describe what the number represents in the problem's context.
By being aware of these common mistakes and implementing these strategies, you can significantly improve your accuracy when working with fractions of a set. Remember, practice and patience are key. Don't get discouraged if you make mistakes they're an important part of the learning process. Keep working through problems, double-check your work, and don't hesitate to ask for help when needed. With time and effort, you'll become more confident and proficient in handling these types of problems.
Conclusion and Next Steps
In summary, this article has explored the crucial concept of fractions of a set, providing a solid foundation for students to build upon. The introduction video serves as an invaluable tool, offering visual representations and clear explanations to enhance understanding. Key points covered include identifying the whole set, determining the fractional part, and calculating the result. To further reinforce these concepts, students are encouraged to practice with various real-world examples and engage in problem-solving activities. Consider working with different set sizes and exploring more complex fractions to deepen your understanding. Remember, mastering fractions of a set is essential for advancing in mathematics and applying these skills to everyday situations. Take the knowledge gained from this article and the accompanying video, and challenge yourself to solve fraction problems in your daily life. By doing so, you'll solidify your grasp on this fundamental mathematical concept and pave the way for future success in more advanced topics.
Introduction to Fractions of a Set: How to Find the Fraction of a Set of Objects
In this guide, we will explore how to find the fraction of a set of objects using a step-by-step approach. This method is useful for understanding how fractions can be applied to groups of items, making it easier to visualize and solve fraction problems.
Step 1: Understanding the Concept of Fractions of a Set
Fractions represent parts of a whole. When we talk about fractions of a set, we are referring to dividing a group of objects into equal parts and then considering a specific number of those parts. For example, if we have a set of 8 jelly beans and we want to find one-fourth of them, we are looking to divide the set into 4 equal parts and then take one of those parts.
Step 2: Identifying the Total Number of Objects
First, determine the total number of objects in the set. In our example, Austin has 8 jelly beans. This total number represents the whole set that we will be working with.
Step 3: Dividing the Set into Equal Groups
Next, we need to divide the set into equal groups based on the denominator of the fraction. The denominator tells us how many equal parts the set should be divided into. For one-fourth, we divide the set into 4 equal groups. Since we have 8 jelly beans, we divide 8 by 4, which gives us 2 jelly beans per group.
Step 4: Selecting the Number of Groups
The numerator of the fraction tells us how many of these equal groups we need to consider. For one-fourth, the numerator is 1, so we take one of the 4 groups. Each group contains 2 jelly beans, so one-fourth of 8 jelly beans is 2 jelly beans.
Step 5: Applying the Fraction to Different Scenarios
Let's consider another example where Austin wants to give three-fourths of his 8 jelly beans to his friends. We follow the same steps: divide the set into 4 equal groups (8 divided by 4 equals 2 jelly beans per group). This time, the numerator is 3, so we take 3 of the 4 groups. Each group has 2 jelly beans, so three-fourths of 8 jelly beans is 6 jelly beans.
Step 6: Using Mathematical Operations
To simplify the process, we can use mathematical operations. For unit fractions (where the numerator is 1), we can simply divide the total number of objects by the denominator. For example, one-fourth of 8 is calculated as 8 divided by 4, which equals 2. For non-unit fractions (where the numerator is not 1), we divide the total number of objects by the denominator and then multiply the result by the numerator. For example, three-fourths of 8 is calculated as (8 divided by 4) multiplied by 3, which equals 6.
Step 7: Visualizing with Models
To help visualize fractions of a set, we can use models such as circles or other shapes. Draw the total number of objects as circles and then group them according to the denominator. Highlight the number of groups specified by the numerator to see the fraction of the set. This visual representation can make it easier to understand and solve fraction problems.
Step 8: Practice and Application
Practice finding fractions of different sets of objects to reinforce the concept. Use various examples and scenarios to apply the steps and become more comfortable with the process. Understanding fractions of a set is a fundamental skill that can be applied to many real-world situations, such as dividing items among friends or calculating portions in recipes.
By following these steps, you can effectively find the fraction of a set of objects and apply this knowledge to various mathematical problems and everyday situations.
FAQs
Here are some frequently asked questions about fractions of a set:
-
What is a fraction of a set?
A fraction of a set refers to a part of a whole group of objects or items. It involves dividing the total number of items in the set by the denominator of the fraction and then multiplying by the numerator to find the specific part.
-
How do I calculate 1/3 of 24 objects?
To find 1/3 of 24 objects, divide 24 by 3: 24 ÷ 3 = 8. Therefore, 1/3 of 24 objects is 8 objects.
-
Can I use fractions of a set in real-life situations?
Yes, fractions of a set are commonly used in everyday life. Examples include dividing a pizza among friends, calculating discounts while shopping, or determining the proportion of ingredients in a recipe.
-
What's the difference between unit fractions and non-unit fractions of a set?
Unit fractions have a numerator of 1 (e.g., 1/2, 1/3, 1/4), while non-unit fractions have numerators greater than 1 (e.g., 2/3, 3/4). For unit fractions, you can simply divide the total by the denominator. For non-unit fractions, you need to divide by the denominator and then multiply by the numerator.
-
How can I improve my skills in working with fractions of a set?
To improve your skills, practice regularly with various set sizes and fractions. Use visual aids like diagrams or objects to represent sets. Apply the concept to real-world scenarios and solve word problems. Additionally, focus on understanding the relationship between the numerator, denominator, and the total set size.
Prerequisite Topics
Understanding fractions of a set is a fundamental concept in mathematics that builds upon several basic mathematical principles. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in basic arithmetic and number sense is crucial for grasping this concept effectively.
To fully comprehend fractions of a set, students should be comfortable with whole numbers and have a solid understanding of division. The ability to divide objects or quantities into equal parts forms the basis for working with fractions of a set. Additionally, familiarity with basic fraction concepts, such as numerators and denominators, is beneficial when exploring this topic.
Another important aspect to consider is the concept of sets themselves. Understanding what constitutes a set and how to group objects or numbers together is essential when working with fractions of a set. This foundational knowledge helps students visualize and manipulate parts of a whole in various contexts.
Moreover, basic counting skills and the ability to recognize patterns play a significant role in mastering fractions of a set. These skills enable students to identify and calculate specific portions of a given set accurately. Developing a strong number sense also aids in estimating and verifying results when working with fractions of a set.
While not explicitly listed as prerequisites, concepts such as multiplication and division of whole numbers are closely related to fractions of a set. These operations are often used when calculating and manipulating fractional parts of a larger group or quantity.
It's worth noting that understanding proportions and ratios can enhance a student's grasp of fractions of a set. These related concepts help in visualizing and comparing different parts of a whole, which is essential when working with fractions in various real-world scenarios.
As students progress in their mathematical journey, the ability to work with fractions of a set becomes increasingly important. This concept serves as a stepping stone to more advanced topics such as percentages, probability, and data analysis. By mastering fractions of a set, students develop critical thinking skills and problem-solving abilities that are applicable across various mathematical disciplines.
In conclusion, while there may not be specific prerequisite topics listed for fractions of a set, a strong foundation in basic arithmetic, number sense, and fundamental fraction concepts is crucial. By building upon these foundational skills, students can confidently approach and master the concept of fractions of a set, paving the way for success in more advanced mathematical studies.

