Addition strategies
Topic Notes
In this lesson, we will learn:
- The addition strategies of: (1) using friendly numbers with adjustment, (2) creating friendly numbers using addends, (3) adding on from left to right, and (4) adding by counting on
- Understanding adding by 9
Notes:
- Method 1: change into a "friendly" number and then adjust (by subtracting)
- Round one of the addends to the nearest multiple of 10
- Then adjust by taking away how much you rounded up by to get the answer

- Method 2: make a "friendly" number using the addends
- Use the numbers that were given for the addition equation
- Move values from one number to the other number to make a multiple of 10
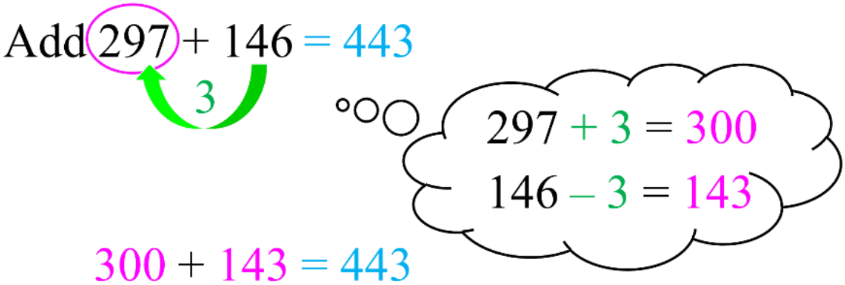
- Method 3: adding from left to right
- Add by going through one place value at a time
- i.e. hundreds of 1st # + hundreds 2nd # + tens of 1st # + tens of 2nd # + . . .

- Method 4: adding by counting on
- Start with the first number, then add the second number one place value at a time
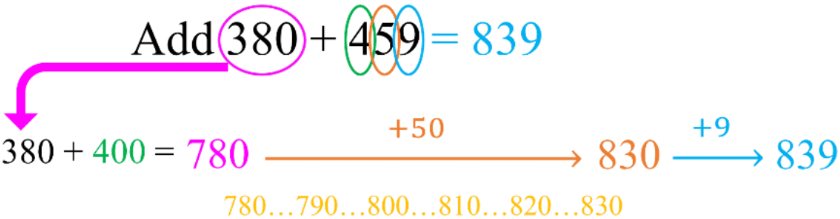
Introduction to Addition Strategies
Welcome to our lesson on addition strategies, an essential component of mental math skills. We'll begin with an introduction video that sets the foundation for understanding these powerful techniques. This video is crucial as it demonstrates how these strategies can significantly enhance your ability to perform calculations quickly and accurately. Throughout this lesson, we'll explore four main addition strategies that will revolutionize your approach to mental arithmetic. These strategies are designed to make addition more intuitive and efficient, allowing you to tackle complex problems with ease. Additionally, we'll delve into the specific technique of adding by 9, a frequently encountered scenario in everyday math. By mastering these strategies, you'll develop a toolkit of mental math techniques that utilize friendly numbers and patterns, enabling you to solve addition problems swiftly and confidently in various real-life situations.
Using Friendly Numbers with Adjustment
The strategy of changing one number into a 'friendly number' and then adjusting is a powerful mental math technique that can significantly simplify complex addition problems. This method, often referred to as the 'friendly numbers' approach, involves rounding one of the numbers to the nearest multiple of 10 and then making a small adjustment to compensate for the rounding. Let's explore this strategy using the example of 199 + 438.
In traditional long addition, we would typically align the numbers vertically and add each column, starting from the right. This method, while reliable, can be cumbersome for mental calculations, especially with larger numbers. The friendly numbers strategy offers a more efficient alternative for quick mental math.
Here's a step-by-step breakdown of how to apply the friendly numbers strategy to 199 + 438:
- Identify the number closest to a multiple of 10. In this case, 199 is very close to 200, which is a friendly number.
- Round 199 up to 200. Our new addition problem becomes 200 + 438.
- Perform the mental addition of 200 + 438, which is much easier than the original problem. This gives us 638.
- Remember that we rounded up by 1, so we need to subtract 1 from our result to get the correct answer.
- 638 - 1 = 637, which is our final answer.
This method is particularly effective because it leverages our ability to work more easily with multiples of 10. By transforming one of the numbers into a friendly number, we simplify the mental calculation process. The small adjustment at the end ensures accuracy while maintaining the efficiency of the method.
Compared to traditional long addition, the friendly numbers strategy offers several advantages for mental math:
- It reduces the cognitive load by working with easier numbers.
- It minimizes the risk of errors that can occur when trying to keep track of multiple columns in your head.
- It's faster, especially for those who practice and become proficient with the technique.
- It encourages a deeper understanding of number relationships and place value.
The friendly numbers strategy can be applied to various addition problems, not just those involving numbers close to multiples of 10. For instance, in a problem like 387 + 156, you could round 387 up to 400 and then subtract 13 from the final result. The key is to choose the rounding that makes the calculation easiest for you.
As with any mental math technique, practice is crucial for mastering the friendly numbers strategy. Start with simpler problems and gradually work your way up to more complex additions. Over time, you'll find that this method becomes second nature, allowing you to perform impressive mental calculations quickly and accurately.
It's worth noting that while this strategy is particularly useful for addition, similar principles can be applied to subtraction, multiplication, and even division problems. By consistently looking for ways to work with friendly numbers, you can significantly enhance your overall mental math abilities.
In conclusion, the friendly numbers strategy with adjustment is a valuable tool in the mental math toolkit. It transforms potentially challenging calculations into more manageable ones by leveraging our natural affinity for multiples of 10. By rounding, performing an easier calculation, and then making a small adjustment, we can solve addition problems quickly and efficiently in our heads. This method not only speeds up mental calculations but also deepens our understanding of number relationships, making it an essential skill for students, professionals, and anyone looking to improve their mental math prowess.
Creating Friendly Numbers Using Addends
The strategy of making friendly numbers using given addends is a powerful mental math technique that can significantly simplify addition problems. This method leverages our understanding of place value and regrouping to create easier-to-manage numbers, ultimately leading to quicker and more accurate mental calculations. Let's explore this strategy in detail using the example of 297 + 146.
When faced with the addition problem 297 + 146, our first step is to identify the "friendly number" we want to create. In this case, 300 is an ideal target as it's a multiple of 100 and easier to work with mentally. To achieve this, we'll move values between the addends, keeping the overall sum unchanged.
Here's how we can apply the friendly number strategy:
1. Identify the difference between 297 and 300: it's 3.
2. Subtract 3 from 146 (the second addend): 146 - 3 = 143.
3. Now our new addition problem becomes: 300 + 143.
This transformation maintains the original sum but creates a much friendlier first number (300) to work with. The key principle here is that we're simply moving value from one addend to the other, keeping the total unchanged.
Let's break down why this method is so effective:
1. Easier mental visualization: 300 is a round number that's simpler to picture and manipulate in our minds.
2. Reduced cognitive load: By creating a multiple of 100, we've eliminated the need to carry over from the tens to the hundreds place.
3. Quicker calculation: 300 + 143 can be solved rapidly as 300 + 100 + 43 = 443.
This friendly number strategy isn't limited to creating multiples of 100. Depending on the problem, you might aim for multiples of 10 or even 1000. The goal is always to transform at least one of the addends into a number that's easier to work with mentally.
Compared to traditional long addition, the friendly number method offers several advantages:
1. Speed: Once mastered, this technique allows for much faster mental calculations, eliminating the need for paper and pencil in many situations.
2. Flexibility: The strategy can be adapted to various addition problems, making it a versatile tool for mental math.
3. Understanding: It reinforces a deeper comprehension of place value and number relationships, enhancing overall mathematical thinking.
4. Reduced errors: By simplifying the problem, there's less chance of making mistakes commonly associated with carrying and regrouping in long addition.
To further illustrate the versatility of this method, consider another example: 58 + 26. Here, we might choose 60 as our friendly number. We'd add 2 to 58 to make 60, then subtract 2 from 26 to get 24. The new, easier problem becomes 60 + 24 = 84.
As with any mental math strategy, practice is key to mastering the friendly number method. Start with simpler problems and gradually increase complexity. Soon, you'll find yourself automatically seeking out these friendly numbers in various addition scenarios.
It's important to note that while this strategy is incredibly useful for mental calculations, it doesn't replace the need to understand and be proficient in standard addition algorithms. Rather, it complements traditional methods, providing a powerful tool for quick estimations and mental math in everyday situations.
In conclusion, the friendly number strategy using addends is a valuable technique in the mental math toolkit. By leveraging our understanding of place value and regrouping, we can transform complex addition problems into simpler, more manageable calculations. This method not only speeds up mental arithmetic but also deepens our comprehension of number relationships, making us more adept and confident in our mathematical abilities.
Adding on from Left to Right
Left to right addition is a powerful mental math strategy that leverages our understanding of place value to simplify calculations. This method, also known as left-to-right addition, involves adding numbers starting from the largest place value and working towards the smallest. It's an efficient approach for mental calculations and can often be faster than the traditional right-to-left method we typically learn in school.
Let's explore this strategy using the example of 242 + 250. In the traditional right-to-left method, we would start with the ones, move to the tens, and finally add the hundreds. However, with left to right addition, we begin with the hundreds place:
- Add the hundreds: 200 + 200 = 400
- Add the tens: 40 + 50 = 90
- Add the ones: 2 + 0 = 2
- Combine the results: 400 + 90 + 2 = 492
This approach differs from traditional addition in several key ways. First, it aligns with how we naturally think about numbers, starting with the most significant digits. Second, it allows us to work with rounded numbers initially, which are often easier to manipulate mentally. In our example, adding 200 and 200 is straightforward, and then we can focus on the smaller components.
The efficiency of left to right addition becomes even more apparent with larger numbers or when dealing with multiple addends. It enables us to quickly estimate the result and adjust our calculation as we go, making it particularly useful for mental math and quick estimations.
Moreover, this method reinforces place value understanding. As we work through each place value separately, we're constantly thinking about the significance of each digit in the number. This deepens our comprehension of the number system and can lead to improved overall mathematical fluency.
While the traditional right-to-left method is crucial for written calculations and understanding carrying operations, left to right addition offers a complementary skill that enhances mental math abilities. By practicing both methods, students and adults alike can develop a more flexible and robust approach to arithmetic.
In conclusion, left to right addition is a valuable addition strategy that leverages our innate understanding of place value. By starting with the largest place value and working our way to the smallest, we can perform mental calculations more efficiently and often with greater speed. This method not only simplifies mental math but also reinforces fundamental mathematical concepts, making it a powerful tool in any mathematician's arsenal.
Adding by Counting On
The 'counting on' strategy is a powerful mental addition technique that leverages our understanding of place value and skip counting. This method is particularly useful for adding larger numbers without the need for pen and paper. Let's explore this strategy using the example of 380 + 459.
To begin, we start with the larger number, 459, and then 'count on' from there, adding each place value of 380 sequentially. Here's how it works:
1. Start with 459
2. Add the hundreds place of 380 (300): 459 + 300 = 759
3. Add the tens place of 380 (80): 759 + 80 = 839
4. Finally, add the ones place of 380 (0): 839 + 0 = 839
The final result is 839. This method allows us to break down the addition into manageable steps, utilizing our ability to quickly add multiples of 10 and 100.
The 'counting on' strategy is especially effective when one of the numbers being added is close to a round number. For instance, if we were adding 395 + 278, we could adjust our approach slightly:
1. Start with 395
2. Add 5 to reach 400 (a round number)
3. Add the remaining 273 to 400
This flexibility makes the 'counting on' method adaptable to various addition scenarios.
One of the key benefits of this strategy is that it reinforces place value understanding. As we add each place value separately, we're constantly thinking about hundreds, tens, and ones. This mental exercise strengthens our overall number sense and makes us more adept at handling larger numbers.
Moreover, the 'counting on' technique naturally incorporates skip counting. When we add tens and hundreds, we're essentially skip counting by 10s and 100s. This connection to skip counting makes the method feel intuitive and builds on skills that many learners already possess.
While 'counting on' is primarily a mental math strategy, it can be supported by visual aids or physical manipulatives in educational settings. For example, a number line can be used to demonstrate the jumps in hundreds, tens, and ones. This visual representation can help learners grasp the concept more easily and transition to performing the calculations mentally.
It's worth noting that the 'counting on' strategy is not limited to addition. It can be adapted for subtraction as well, where it's often referred to as 'counting up' or 'counting back'. This versatility makes it a valuable tool in a learner's mathematical toolkit.
As with any math strategy, practice is key to mastering the 'counting on' method. Encourage learners to start with simpler problems and gradually work their way up to more complex additions. With time and practice, this technique can significantly enhance mental math abilities and overall numerical fluency.
Understanding Adding by 9
Adding by 9 is a special case in mental math that can be simplified using a clever strategy. This technique not only makes calculations easier but also ties into the broader concept of friendly numbers. Let's explore why adding 10 and then subtracting 1, and how this approach can significantly speed up mental calculations.
When we add 9 to any number, we're essentially adding 10 and then adjusting the result by subtracting 1. This works because 9 is just one less than 10, which is a much friendlier number to work with mentally. For example, if we want to add 9 to 24, instead of directly adding 9, we can add 10 to get 34, and then subtract 1 to arrive at the correct answer of 33.
This strategy is particularly useful because our number system is based on 10, making it easier to add multiples of 10. By converting the problem of adding 9 into adding 10 and subtracting 1, we're leveraging this base-10 system to our advantage. Let's look at a few more examples to illustrate this concept:
- 37 + 9 = 37 + 10 - 1 = 47 - 1 = 46
- 52 + 9 = 52 + 10 - 1 = 62 - 1 = 61
- 85 + 9 = 85 + 10 - 1 = 95 - 1 = 94
This approach relates directly to the friendly numbers strategy in mental math. Friendly numbers are those that are easy to work with, typically multiples of 10 or 100. By transforming the addition of 9 into an operation involving 10, we're essentially converting an unfriendly number (9) into a friendly one (10), making the calculation more manageable.
The beauty of this method lies in its simplicity and speed. Once mastered, it allows for quick mental calculations involving 9, which can be particularly useful in everyday situations. This strategy can be extended to other numbers close to multiples of 10. For instance, adding 8 can be thought of as adding 10 and subtracting 2, while adding 11 can be seen as adding 10 and then adding 1.
Incorporating this technique into your mental math toolkit can significantly enhance your calculation speed and accuracy. It's a prime example of how understanding the properties of numbers and leveraging friendly numbers can simplify what might otherwise be complex mental arithmetic. By practicing this method, you'll find that adding 9 becomes almost as effortless as adding 10, making a wide range of calculations much more manageable in your head.
Practicing Addition Strategies
To master mental math practice addition problems, practice is key. Here's a set of problems to help you hone your skills, ranging from easy to challenging. Remember, try different strategies to find what works best for you!
1. Breaking Numbers Apart
- 24 + 38
- 56 + 27
- 135 + 246
Solution for 56 + 27:
Step 1: Break apart 27 into 20 + 7
Step 2: Add 56 + 20 = 76
Step 3: Add 76 + 7 = 83
2. Compensation Method
- 49 + 32
- 78 + 26
- 199 + 45
Solution for 78 + 26:
Step 1: Round 78 up to 80 (add 2)
Step 2: 80 + 26 = 106
Step 3: Subtract the 2 we added: 106 - 2 = 104
3. Making Tens
- 8 + 7
- 28 + 15
- 67 + 36
4. Doubles and Near Doubles
- 6 + 7
- 25 + 26
- 48 + 50
Solution for 25 + 26:
Step 1: Recognize 25 + 25 = 50 (double)
Step 2: Add 1 more: 50 + 1 = 51
5. Adding Up in Chunks
- 23 + 45 + 12
- 87 + 56 + 33
- 124 + 236 + 140
Challenge yourself to solve these problems using different strategies. For example, try solving 49 + 32 using both the compensation method for addition and breaking numbers apart. Which feels more natural to you? Remember, mental math is about finding efficient ways that work for your thinking style. As you practice, you'll discover which strategies feel most comfortable and lead to quicker solutions. Don't be discouraged if some problems seem difficult at first with consistent practice, your mental math skills will improve dramatically. Keep challenging yourself with increasingly complex problems, and soon you'll be performing impressive calculations in your head with ease!
Conclusion
In this lesson, we've explored essential addition strategies that enhance mental math skills. The introduction video provided a solid foundation for understanding these concepts. Key points include breaking numbers into manageable parts, using landmark numbers, and applying the commutative property. These strategies not only improve calculation speed but also deepen number sense. Remember, mental math is a valuable skill that extends beyond the classroom. By practicing these addition strategies regularly, you'll become more confident and efficient in your daily math encounters. Whether you're shopping, cooking, or solving complex problems, these techniques will prove invaluable. We encourage you to continue exploring and refining your mental math abilities. Challenge yourself to use these strategies in various situations, and you'll soon see remarkable improvements in your mathematical prowess. Embrace these tools, and watch your mental math skills soar to new heights!
Introduction to Addition Strategies: Mental Math and Sums of 10
In this guide, we will explore various addition strategies that can help you perform mental math more efficiently. Specifically, we will focus on the importance of zeros in place values and how to make sums of 10. These strategies are essential tools for simplifying addition problems and enhancing your mental arithmetic skills.
Step 1: Understanding the Role of Zeros in Place Values
When adding numbers, zeros in place values can significantly simplify the process. For example, consider the addition problem 40 + 9. By aligning the numbers by their place values, you can see that:
- In the ones column: 0 + 9 = 9
- In the tens column: 4 + 0 = 4
Therefore, 40 + 9 = 49. The presence of zeros makes it easier to add the numbers mentally because you only need to focus on the non-zero digits.
This concept can be extended to larger numbers as well. For instance, when adding 205 + 160, you can quickly identify the zeros in the place values and perform the addition mentally:
- In the hundreds column: 2 + 1 = 3
- In the tens column: 0 + 6 = 6
- In the ones column: 5 + 0 = 5
Thus, 205 + 160 = 365. Zeros are your best friends in mental math because they simplify the addition process.
Step 2: Making Sums of 10
Another powerful tool in mental math is making sums of 10. Multiples of 10 always end in zero, which makes them easier to work with. To master this strategy, you need to be familiar with the number pairs that add up to 10:
- 1 + 9
- 2 + 8
- 3 + 7
- 4 + 6
- 5 + 5
These pairs are essential for quickly making sums of 10. For example, if you encounter the number 7 and need to add up to 10, you know that you need a 3. Similarly, if you have a 6, you need a 4 to make 10.
Understanding these pairs allows you to break down more complex addition problems into simpler parts. For instance, if you need to add 27 + 13, you can break it down as follows:
- First, add the tens: 20 + 10 = 30
- Then, add the ones: 7 + 3 = 10
Combining these results, you get 30 + 10 = 40. By making sums of 10, you can simplify the addition process and perform calculations more quickly in your head.
Step 3: Applying the Commutative Property of Addition
The commutative property of addition states that the order in which you add numbers does not affect the sum. This property is particularly useful when making sums of 10. For example, 4 + 6 is the same as 6 + 4, and both equal 10.
By leveraging this property, you can rearrange numbers to make the addition process more straightforward. For instance, if you need to add 8 + 2 + 5, you can rearrange the numbers to make a sum of 10 first:
- 8 + 2 = 10
- Then, add the remaining 5: 10 + 5 = 15
Using the commutative property in combination with making sums of 10 can significantly enhance your mental math skills and make addition problems more manageable.
Step 4: Practice and Application
To master these addition strategies, practice is essential. Start with simple problems and gradually work your way up to more complex ones. Use the following exercises to reinforce your understanding:
- Add numbers with zeros in place values, such as 50 + 30 or 200 + 400.
- Practice making sums of 10 with different number pairs, such as 3 + 7 or 4 + 6.
- Apply the commutative property to rearrange numbers and simplify addition problems.
By consistently practicing these strategies, you will develop a strong foundation in mental math and be able to perform addition more efficiently.
FAQs
-
What are the main addition strategies covered in this lesson?
The main addition strategies covered in this lesson are:
- Using friendly numbers with adjustment
- Creating friendly numbers using addends
- Adding from left to right
- Adding by counting on
- Understanding adding by 9
-
How does the friendly numbers strategy work?
The friendly numbers strategy involves rounding one number to a multiple of 10 or 100 to make the calculation easier. For example, when adding 199 + 438, you would round 199 up to 200, add 200 + 438 = 638, and then subtract 1 to get the final answer of 637. This method simplifies mental calculations by working with easier numbers.
-
What is the benefit of adding from left to right?
Adding from left to right aligns with how we naturally think about numbers, starting with the most significant digits. It allows us to work with rounded numbers initially, which are often easier to manipulate mentally. This method is particularly useful for quick estimations and mental math, as it enables us to get a sense of the answer more quickly than traditional right-to-left addition.
-
Why is adding by 9 considered a special case?
Adding by 9 is considered a special case because it can be simplified by adding 10 and then subtracting 1. This strategy leverages our base-10 number system, making calculations easier. For example, 24 + 9 can be calculated as 24 + 10 - 1 = 34 - 1 = 33. This method is faster and more efficient for mental calculations.
-
How can I improve my mental math skills using these strategies?
To improve your mental math skills using these strategies:
- Practice regularly with a variety of problems
- Start with simpler calculations and gradually increase difficulty
- Apply these strategies in real-life situations
- Challenge yourself to solve problems using different methods
- Focus on understanding the concepts rather than memorizing procedures
Consistent practice and application will help these strategies become second nature, significantly enhancing your mental math abilities.
Prerequisite Topics for Addition Strategies
Understanding addition strategies is crucial for developing strong mathematical skills. However, to truly grasp and excel in addition techniques, it's essential to have a solid foundation in certain prerequisite topics. Two key concepts that play a vital role in mastering addition strategies are place value and rounding numbers.
Place value is fundamental to understanding how numbers work in our decimal system. It helps students recognize the significance of each digit in a number based on its position. When applying addition strategies, a strong grasp of place value enables learners to break down numbers effectively, making the addition process more manageable and logical. For instance, when adding larger numbers, understanding place value allows students to align digits correctly and carry over values to the appropriate columns.
Moreover, place value knowledge is essential for mental math techniques. It empowers students to decompose numbers quickly, facilitating faster and more efficient addition. For example, when adding 38 and 45, a student with a solid understanding of place value can easily break it down into 30 + 40 and 8 + 5, making the calculation more straightforward.
Another crucial prerequisite topic for addition strategies is rounding numbers. This skill is particularly valuable when estimating sums or checking the reasonableness of answers. By rounding numbers before adding, students can quickly approximate results, which is especially useful in real-life situations where precise calculations may not be necessary or practical.
Understanding rounding numbers also aids in developing number sense and flexibility in working with numbers. This flexibility is crucial when applying various addition strategies, as it allows students to choose the most efficient method based on the numbers involved. For instance, when adding 398 and 605, rounding to 400 and 600 can simplify the mental calculation process.
By mastering these prerequisite topics, students build a strong foundation for learning and applying various addition strategies. The ability to understand place value and proficiency in rounding numbers not only enhances addition skills but also contributes to overall mathematical competence. These fundamental concepts serve as building blocks for more advanced mathematical operations and problem-solving techniques.
In conclusion, recognizing the importance of prerequisite topics like place value and rounding numbers is crucial for students aiming to excel in addition strategies. By investing time in strengthening these foundational skills, learners set themselves up for success in more complex mathematical concepts and real-world applications of addition.

