The invertible matrix theorem
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/2
Intros
Lessons
- Characterizations of Invertible Matrices Overview:
- The Invertible Matrix Theorem
• only works for n×n square matrices
• If one is true, then they are all true
• If one is false, then they are all false
- How to apply the Invertible Matrix Theorem
• Showing a Matrix is invertible
• Shortcuts to know certain statements
0/8
Examples
Lessons
- Showing a Matrix is invertible or not invertible
Is the following matrix invertible?
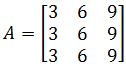
- Is the following matrix invertible? Use as few calculations as possible.

- Understanding the Theorem
Assume that A is a square n×n matrix. Determine if the following statements are true or false:- If A is an invertible matrix, then the linear transformation x→Ax maps Rn onto Rn.
- If there is an n×n matrix C such that CA=I, then there is an n×n matrix D such that AD=I
- If the equation Ax=0 has only the trivial solution, then A is not invertible.
- If the equation Ax=0 has a non-trivial solution, then A has less than n pivots.
- Can a square matrix with two identical rows be invertible? Why or why not?
- Let A and B be n×n matrix. Show that if AB is invertible, so is B.
Free to Join!
StudyPug is a learning help platform covering maths and science from primary all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
The invertible matrix theorem
What is an invertible matrix
What does it mean for a matrix to be invertible? Throughout past lessons we have already learned that an invertible matrix is a type of square matrix for which there is always another one (called its inverse) which multiplied to the first, will produce the identity matrix of the same dimensions as them.
In other words, the matrix is invertible if and only if it has an inverse matrix related to it, and when both of them are multiplied together (no matter in which order), the result will be an identity matrix of the same order. During this lesson we will discuss a list of characteristics that will complement this invertible matrix definition, this list is what we call the invertible matrix theorem.
But before let us go through a quick review on how to invert a 2x2 matrix to explain this concept a little better, we will call this 2x2 matrix X. Remember from past lessons that X is said to be an invertible 2x2 matrix if and only if there is an inverse matrix X−1 which multiplied to X produces a 2x2 identity matrix, which is mathematically defined in the condition:
Inverting matrix X is quite the simple task, but if we want to work with inverses of higher order matrices we have to remember that the condition shown in equation 1 still holds when n is higher than 2, and so, in general, we know we can invert a matrix of n×n dimensions which we define as A if the following condition is met:
Keep always in mind that there is a difference between an invertible matrix and an inverted matrix. And invertible matrix is any matrix which has the capacity of being inverted due to the type of determinant it has, while an inverted matrix is one which has already passed through the inversion process. If we look at equation 2, A would be referred as the invertible matrix and A−1 would be the inverted matrix. This is just to denote the matrices are not the same, and so, while working through problems it is important to remember which is your original one.
On the next section we will learn how to tell if a matrix is invertible and when is a matrix not invertible by using the invertible matrix theorem.
What is the invertible matrix theorem
So what is the Invertible matrix theorem? This theorem states that if A is a n×n square matrix, then the following statements are equivalent:
- A is an invertible matrix.
- A is row equivalent to the n×n identity matrix.
- A has n pivot positions.
- The equation Ax=0 has only the trivial solution.
- The columns of A form a linearly independent set.
- The equation Ax=b has at least one solution for each b in Rn.
- The columns of A span Rn.
- The linear transformation x→Ax maps Rn onto Rn.
- There is an n×n matrix C such that CA=I.
- There is an n×n matrix D such that AD=I.
Therefore, if all of these statements are equivalent, the rule is that for a given matrix A the statements are either all true or all false. The full invertible matrix theorem contains more than these 10 statements, but we have selected those which are most commonly used.
In a nutshell, the invertible matrix theorem is just a set of statements describing the properties a matrix either has or not, and once one of them applies to a given matrix, all of the others should follow because they are either consequences or requirements for all of the other statements to be true.
Instead of going through the process of how to invert a matrix, this theorem allows us to know if inverting a 2x2 matrix (or any other square matrix for that matter) is possible or not beforehand, sometimes saving us from tedious calculations. For this reason, the next section will be dedicated to describe the invertible matrix theorem explained through each of the 10 selected statements for this lesson.
Invertible matrix theorem explained
As mentioned before, the invertible matrix theorem is just a set of many statements which buildup on each other based on the fact that a matrix is either invertible or not. Therefore during this section we will go over each of the ten statements we have selected for our lesson (remember, there are many more!) and say a little bit about them in order to try and explain them or at least put them into context.
During the final section of this lesson, we will look at some proofs with a few exercise problems we will work through.
1. A is an invertible matrix.
At this point you are very familiarized with an invertible matrix, we even dedicated the first section of this lesson to define it again (as it has been done in a few lessons before). The fact that a matrix is either invertible or not, will be the first step that unchains many other characteristics that can be attributed to the matrix if it is invertible, or that the matrix will not have if it is not invertible.
So if a square matrix named A is indeed invertible (there exists another square matrix of the same size which multiplied to A will produce the identity matrix of the same size as them), then all of the next statements are true for this matrix A (and its inverse, for that matter).
2. A is row equivalent to the n×n identity matrix.
A row equivalent set of matrices are those in which one can be row reduced into the other one using the the three types of matrix row operations. Therefore, if a matrix is invertible, it means that it can be reduced into its reduced echelon form which will be the identity matrix of the same size.
3. A has n pivot positions.
This statement is easily understandable after statement number two: once you have reduced the original provided matrix A into its reduced echelon form, you will have the same amount of pivots as you have columns (and rows) in the square matrix.
4. The equation Ax=0 has only the trivial solution.
Statement 4 is just a consequence of our next one.
Remember that for a collection of vectors (which can be squeezed together into a matrix) to be linearly independent, it means that the result from the matrix equation Ax=0 will be a trivial solution.
In other words, the vector x that is being multiplied to the square matrix A is a vector with all zero components (is a zero vector!), and that is why this matrix equation of Ax is equal to zero (so A is not all zeros!). And the conclusion is our next statement:
5. The columns of A form a linearly independent set.
Providing that the solution to the matrix equation Ax=0 results in x being a zero vector, we conclude that the column vectors contained in matrix A are all linearly independent from each other, thus, are a linearly independent set.
This becomes clear from statement 2 where we say that all of the invertible matrices can be row reduced into the identity matrix of its same size, because it means you can isolate the value of the variables contained in those contained vectors.
Simply said, the column vectors contained within the given matrix A are not multiples of each other and are not from a linear combination of each other in any way. That is how you can obtain the identity matrix while row reducing, because you can isolate all of the different variables from the vectors inside the matrix and obtain their straightforward solution value when solving a matrix equation (through forming an augmented matrix and then row reducing) without having to transcribe the reduced echelon form of the matrix into a system of equations to finish solving by substitution.
6. The equation Ax=b has at least one solution for each b in Rn.
This is what we just explained in our past statement. Given that a matrix is invertible, it means it can be thought as a system of equations in which you can solve all of the final values of their variables through row reduction into reduced echelon form without the need for further computation afterwards.
In order to find the values of the variables from such a system, we are to solve the matrix equation Ax=b, and in this equation we are for find at least one solution for each variable (components on the x vector) just as when b is zero ( but remember, if b=0 we go back to statement 4 where x and all of its components are zero, when b is different than zero, then we will obtain different values for the components of x).
7. The columns of A span Rn.
Statement seven says that the column vectors contained in a given square matrix A, which is invertible, must span in the coordinate vector space Rn. This is understandable, remember n is the amount of columns of A, therefore: this statement means that the vectors in the matrix always contain the same amount of different variables (and thus, they will comprise through the same amount of dimensions and require the same different dimensional planes in the real coordinate space Rn to be graphically represented) as the amount of columns contained in the matrix. In other words, if matrix A is a 2x2 matrix, then it means the column vectors are two-dimensional and span in a two-dimensional real coordinate space R2, or, if matrix A is a 3x3 matrix, then it means the column vectors are three-dimensional and span in a three-dimensional real coordinate space R3.
8. The linear transformation x→Ax maps Rn onto Rn.
Statement 8 is just a straight consequence of statement 7. This basically means that if you have a vector x with n amount of components (basically, n number of entries in the vector), the transformation Ax will result in a column vector with n amount of entries too, and thus it can be mapped in the real coordinate space of n dimensions Rn.
In other words, if x is a vector with two components (2 entries), the linear transformation Ax can only be performed with A being an invertible matrix 2x2 (due to matrix multiplication requirements) and the result will be a vector with two components too, therefore, it can be mapped in R2.
If the vector x contains three components (3 entries), the linear transformation Ax can only be performed with A being a 3x3 matrix and the result will be a vector with three components too, therefore, it can be mapped in R3.
9. There is an n×n matrix C such that CA=I.
Statement 9 tells us that since A is an invertible matrix, then there must be a matrix C which multiplied to matrix A will produce the identity matrix of the same size as A. This is due the condition of invertibility that we have seen in past lessons.
10. There is an n×n matrix D such that AD=I.
As we saw in our lesson about the inverse of a 2x2 matrix, if a matrix has an inverse, the multiplication of such inverse and the original matrix will produce the identity matrix of the same size as the original square matrix. The condition is shown in the next equation:
This means that the matrix C from statement 9 is equal to matrix D from statement 10.
The only reason why statements 9 and 10 tend to be written separated is due the conditions for matrix multiplication. Remember that matrix multiplication is not commutative, and so, it is not intuitive for matrices C and D to be the same. Nevertheless, given that we are talking about an inverse matrix, this is an special case in which matrix multiplication happens to be commutative, and we have talked about this in past lessons. This particular counter-intuitive (and yet, obvious after studying past lessons) dependence of statement 9 and 10, is a clear example on how all of the conditions listed in the theorem are codependent of one another, and why it is very important that if one of them does not fit with the matrix given, it means none of them will.
In summary, what the invertible matrix theorem means is that if we define an invertible matrix, this matrix MUST meet all of the other properties mentioned throughout the theorem. This is due the relationship of each of these characteristics of a square matrix with each other, in other words, the invertible matrix theorem lists a set of properties of square matrices which depend on one another, and thus, if one happens in a matrix, all of the rest of them will do too.
This is very useful when proving a matrix is invertible, for example, if we want to obtain the inverse of a 2x2 matrix without using the long methods described in past lessons, we can just check the matrix in question against all of the statements in the theorem. If we can easily deduct that one of them is met, this will be what makes a matrix invertible since all of the other statements from the theorem will be true too.
While determining if a matrix is invertible, or while inverting a matrix itself, if you are ever in the situation where, with a given matrix, you find that some of the invertible matrix theorem properties are met and some of them are not, go back and re-check all of your work since this means there must be a mistake in the calculations and they need to be corrected.
Proof of invertible matrix theorem In order to show proof of the invertible matrix theorem we will work through a variety of cases where you can use the 10 selected statements to deduct when is a matrix invertible and when is not. These invertible matrix theorem examples are much simpler than our usual problem exercises and often, will not require mathematical calculations, just simple deduction.
Example 1
Given matrix A as defined below:
Is A an invertible matrix?
Instead of trying to invert matrix A by methods such as the row operation reduction which can be quite long, let us look at what the invertible theorem says and check for one of its statements to be useful.
If we look at statement number 5: The columns of A form a linearly independent set. we can quickly observe if A can be inverted or not. So, let us obtain the column vectors which conform matrix A:

As you can see, the vectors in the set are multiples of each other, for example if you multiply the first vector by 2, you obtain the second vector; if you multiply the first vector by 3 you obtain the third vector. Therefore, these vectors are NOT linearly independent with each other, and so the statement number 5 from the theorem does not hold in this case.
If statement 5 is not true for this matrix A, then none of them are, therefore A is a non invertible matrix.
Example 2
Is the following matrix invertible? Use as few calculations as possible.
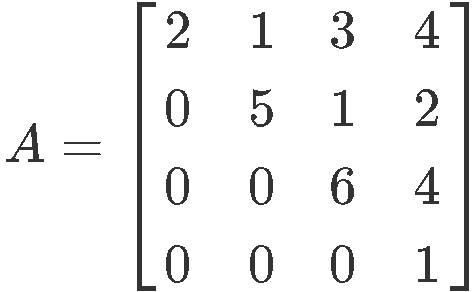
If you notice on this case the 4x4 matrix A is in echelon form, so we can quickly use statement 3 to check for invertibility. Statement 3 says: A has n pivot positions.
For this case, n=4, and if you look at equation 6, A has 4 pivot positions:
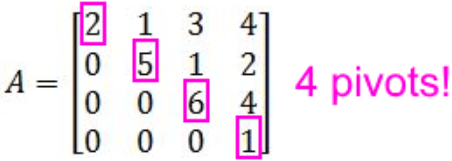
Therefore, A is invertible because statement 3 holds true, and that means statement 1 also holds true.
Example 3
Assume that A is a square n×n matrix. Determine is the following statements are true of false:- If A is an invertible matrix, then the linear transformation x→Ax maps Rn onto Rn
This statement is true since is saying that if statement 1 holds true, then statement 8 holds true too.
- If there is an n×n matrix C such that CA=I, then there is an n×n matrix D such that AD=I.
This statement is true since is saying that if statement 9 holds true, then statement 10 holds true too.
- If the equation Ax=0 has only the trivial solution, then A is not invertible.
False, this statement is saying that if statement 4 is true, then statement 1 is false, which is not possible, either all of the statements in the invertible matrix theorem are met, or not of them are.
- If the equation Ax=0 has a non-trivial solution, then A has less than n pivots.
The first part of this statement is opposite to statement 4 from the theorem, therefore this means the matrix in this case is not invertible. The second part of this statement is also contrary to what is said in another statement from the theorem (this case statement 3), and thus this aso means that the matrix for this case is not invertible. Since both parts of the statement are contrary to the invertible matrix theorem, then this is possible, and so it is true.
To finish up this lesson we recommend you to take a look at the next handout where you will find a complete summary on the inverse of a matrix and which can be useful for your independent studies. To add to your resources on the properties of invertible matrices, visit this last link for an explained example on how to use the invertible matrix theorem.
So this is it for the lesson of today, well see you in our next one!
The Invertible Matrix Theorem states the following:
Let A be a square n×n matrix. Then the following statements are equivalent. That is, for a given A, the statements are either all true or all false.
1. A is an invertible matrix.
2. A is row equivalent to the n×n identity matrix.
3. A has n pivot positions.
4. The equation Ax=0 has only the trivial solution.
5. The columns of A form a linearly independent set.
6. The equation Ax=b has at least one solution for each b in Rn.
7. The columns of A span Rn.
8. The linear transformation x→Ax maps Rn onto Rn.
9. There is an n×n matrix C such that CA=I.
10. There is an n×n matrix D such that AD=I.
There are extensions of the invertible matrix theorem, but these are what we need to know for now. Keep in mind that this only works for square matrices.
Let A be a square n×n matrix. Then the following statements are equivalent. That is, for a given A, the statements are either all true or all false.
1. A is an invertible matrix.
2. A is row equivalent to the n×n identity matrix.
3. A has n pivot positions.
4. The equation Ax=0 has only the trivial solution.
5. The columns of A form a linearly independent set.
6. The equation Ax=b has at least one solution for each b in Rn.
7. The columns of A span Rn.
8. The linear transformation x→Ax maps Rn onto Rn.
9. There is an n×n matrix C such that CA=I.
10. There is an n×n matrix D such that AD=I.
There are extensions of the invertible matrix theorem, but these are what we need to know for now. Keep in mind that this only works for square matrices.
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



