What is the wronskian?
After having determined the two solutions to a linear homogeneous second order differential equation with methods seen in past lessons, we form a general solution to the differential equation by adding them together and we could call it done. In reality, there are still a few things to check on this general solution, such as if this solution still is able to satisfy the conditions given to the original differential equation efficiently, or if the two preliminar solutions are linearly independent. In this case we make use of a method called the wronskian to help us out gather more information about the solution to our differential equations.
The wronskian is a simple and straight forward tool to find out final concise information regarding the solutions to differential equations. By using an algebraic approach combined with derivations, and following the conditions established on each differential equation's case, the wronskian can let you know the final solution of the problem.
One of the greatest advantages of the wronskian is that it can be used with higher order differential equations, and so, for any nth order differential equation, as long as you know n-1 solutions, the wronskian aids in solving for the last general solution while adding information on the rest of them, such as linear independence, plane location, etc.
It is important to note that since we usually look at the values of the wronskian determinant to make inferences about the linear dependency of the preliminary solutions of the differential equation, we need to be careful with the interpretations we give to results. A popular misconception in past times was when the value we obtained for the wronskian was zero, since thanks to published errors throughout history, it has been taken as an unequivocally sign of linear dependence but it has long been proved the contrary for certain cases and conditions. For that, we will be looking for the wronskian to have values different to zero to assert results in a much less confusing manner, and without further ado, let us take a look at what precise information can be obtained from the wronskian and in which circumstances.
What does the wronskian tell you?
When having an initial value problem with certain conditions given, for example one looking to solve a second order differential equation, and having found two solutions, the wronskian will be computed to prove if these known solutions are a fundamental set of solutions. That means, to see if these solutions satisfy the initial conditions of the problem and can give the most efficient final general solution of the problem.
When we compute the wronskian of the two functions involved in the preliminary solutions and the determinant result is different than zero, then we know we have the fundamental solution for the differential equation by adding the two preliminary solutions. Once a fundamental solution for a problem has been found, the numerical solution can be easily obtained, and you can be sure that the result will comply with the original boundary conditions.
How to find the wronskian?
In simple terms, the wronskian is a determinant of a set of functions and their derivatives. Now let us talk about how does this actually looks like and how do we solve it. Although the wronskian method in itself is fairly simple since it resembles algebraic notations used before, we will show it step by step on these next paragraphs so it makes sense not only in its meaning but also in its process.
In order to find a wronskian you first need to have a set of n functions, where n can be any number and it represents the total amount of functions contained in the set you are about to work with
Let us note that for simplicity, in the examples worked on this article we will use n up to 3, but in real world scenarios n can grow as much as needed for a set of functions to be resolved. There are many different ways to simplify processes in which n is a big quantity and there are also other methods for solving differential equations, we shall leave those for later and concentrate in simple examples with as many as 3 functions and therefore two derivatives for each in the wronskian for the moment.
Going back to the wronskian method, the n functions can be real or complex, and you are going to write them down on a matrix-like fashion, this representation is called the wronskian matrix and it looks like this:
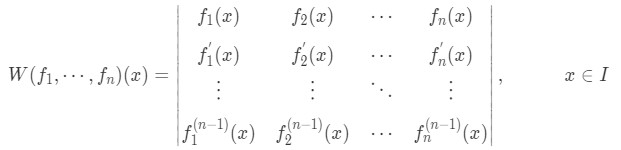
Note, the functions are the top row of the matrix notation, each function will have a column that will get filled with its derivatives. Therefore, the second, third and following rows below the top in the matrix are the first, second and so on derivatives of each function. You will derive each function as many as n-1 times to complete the matrix box, in other words, if you have 5 functions (in which case n=5) then you will derive each of these functions 4 times (because n-1=5-1=4, 4 times), that will give you a matrix box with five columns, where each column is a function, and then a total of five rows too because the first row is the function, and the next four rows are the first, second, third and fourth derivative of each function.
For this last described example, you would end up with a 5x5 matrix which you would have to solve its determinant for, this result is what we have been calling the wronskian determinant. The whole mathematical representation seen in figure 1 is the complete wronskian formula, and it serves to complete the process with any amount of functions, or any n.
As we mentioned before, for simplicity during this article we will work through examples with n as big as 3, resulting in a 3x3 wronskian matrix, but remember you can use the wronskian method to solve for sets of functions much bigger than that.
But before we solve an actual problem using the Wronskian, we need to make sure to revise the method to work out a determinant, since is the exact same procedure just changing the type of variables and quantities you have to work with. So, for a simple 2x2 matrix you can solve it using the next notation:
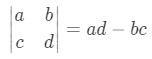
Example:
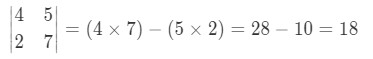
Raising the number of variables in the matrix to make it a 3x3 problem, the formula goes as follows:
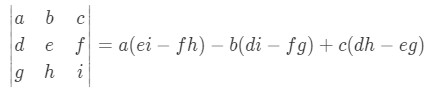
Example:

This was just a quick review on how solving matrix determinants, if you want to have a more thorough discussion on matrices please visit the Study Pug section on how to solve the determinants of simple matrix operations.
Now let us go to the topic in question here: solving the Wronskian determinants. So let us start with the simplest type of example, where you have a set of two functions which happen to be the solutions of a linear homogeneous second order differential equation.
We start with the linear homogeneous second order differential equation, which usually we find in the form of:
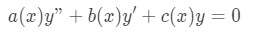
Assuming the two found solutions of the above equation are: and we can automatically obtain a general solution by adding them together:
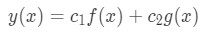
Having this, we use the wronskian to see whether and are linearly independent.
Although we already know the formula for the wronskian (go back to figure 1 on this article), in this case we need it in its simplest form, so we simplify the formula to a 2x2 wronskian matrix which in this case looks like:
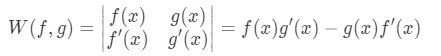
And so, if when having the two solutions and then we say that and form a fundamental set of solutions and therefore the general solution we found before is a fundamental solution itself, we are now ready to plug numerical values for the problem if they are given and find a numerical solution.
To finalize this section, let us solve an example where we already know the functions for the two preliminary solutions of a certain differential equation, and these two functions are:

So the question is, are these two independent? Will they form a fundamental set of solutions? Let us compute their wronskian!
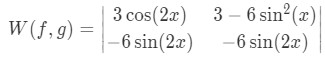
In order to arrive to this matrix, the most complicated part in this case will be to solve the derivative of g(x), so please check out the next quick explanation of it:

this last part was solved using the identity
Now to solve the wronskian:
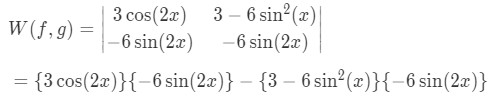
Where we use the trigonometric identity of
so that we transform the term
And so the final solution to our wronskian is:
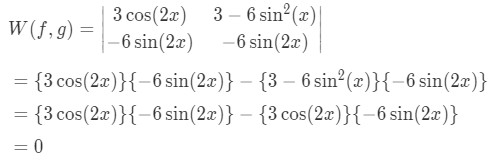
So since the Wronskian is equal to zero, this means that this set of solutions we call and do not form a fundamental set of solutions.
In this particular case it is very easy to prove how these two functions are linearly dependent, if we go back to look at them:

And after working through the wronskian with trigonometric identities, we know that we can write in a different form:
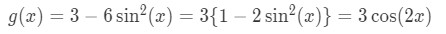
So in this case: ! and our set of solutions cannot be fundamental since we just happened to find the same solution twice just with a different written form.
To complement your learning, make sure to check out the videos on top of this article at the StudyPug website, where you will find this example and others.
The Wronskian and linear independence
We have mentioned before we will obtain information about a set of fundamental solutions to a differential equation using the wronskian and information about their linear dependence or independence, but what do we mean by a set of functions to be linearly independent?
It is said that a set of functions if linearly dependent if one of those functions can be written in terms of the others, or if one of the functions can be produced by a linear combination of the others. This means if one function can be produced by adding the others, or by being a multiple, or by being "proportional" to the others, etc. If none of the functions in the set can be produced or expressed as some form of combination of the others included in the set, or are proportional to any of the other functions in the set, then the functions are linearly independent.
In mathematical terms, for a set of a finite number of functions (which could graphically be represented as vectors) we say they are linearly dependent on an interval if there are also a finite number of constants (scalars) where at least two of them will not be zero such that the next relationship:
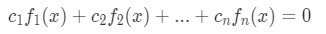
can be re written as:
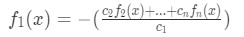
Notice that if all the constants were to be zero, then the two sides of the equation would become zero, and so it would mean that none of the functions can be written as a combination of the others and therefore they are linearly independent from each other. You can always study the process of testing for linear dependence of vectors if you need a quick review on the topic.
Knowing this we can now test the dependence of functions with the wronskian. When the result of the wronskian determinant is not equal to zero, the functions are linearly independent.
For example if we have the set of the next three functions:
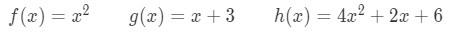
We compute their wronskian determinant:
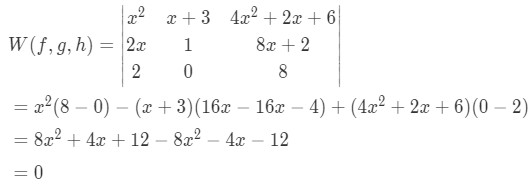
Since the wronskian is equal to zero, this gives us a clue that the functions may be linearly dependent (or in other words, they might not be linearly independent). In this case, their linear dependence is easily proved by combining two of the functions to produce the third one: or so the functions are linearly dependent without a doubt.
To summarize the important points of the Wronskian and linear independence:
Two linearly dependent functions will have a wronskian equal to zero, but not all functions to which their wronskian is equal to zero are dependent. Therefore, if you obtain a wronskian equal zero, you have a clue that the functions might be linearly dependent of each other, but you have to prove it in some other fashion.
If a set of functions have a wronskian different to zero, then these functions are linearly independent of each other.
For examples using this and other methods while solving second order differential equations on physical problems, we recommend you to take a look at the section on applications of second order differential equations at the StudyPug website. You can also take a look at this thorough explanation of linear independence and the wronskian.
Let's assume that we've found two solutions to the above differential equation, and .
And the general solution will be of the form:
We can us the Wronskian to see whether and are linearly independent
The Wronskian is defined as:
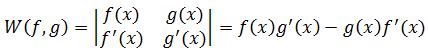
If we have two solution, and , and , then we say that and form a fundamental set of solutions, and the general solution will indeed be of the form:






