Convolution integral
At this point we have talked about calculating Laplace transforms and inverse Laplace transforms extensively. Thus, the purpose of the lesson for today will be to focus on a new tool to use for cases in which solving differential equations with the Laplace transform (or in general) is not possible through other methods such as partial fractions. Such cases will usually involve the multiplication of two Laplace transforms for which you have to solve in the most efficient manner, and that is through something we call the convolution integral.
Define convolution
So what is convolution? In simple terms, convolution refers to the process of combining two expressions to produce a new one. But this is not just a simple algebraic operation, convolution as a general process is very important in our nowadays technology-dependant world due its application on digital signal processing. On this day an era where we function through masses of number sequences and codes filled with information, sent through signals traveling, being received and transferred all over the world, convolution as a method of producing an information filled, time invariant signal from a set, is one of the most important techniques out there for communications, security and data processing in general.
Convolution integral signals and systems
Mathematically speaking, we have already seen in lessons about the Heaviside step function and the Dirac Delta function that we can use expressions (equations) to describe and represent digital signals (we usually think on them in time domain and so you will see most functions happen to be noted as functions of t, but they can have any type of domain); and so, convolution is a mathematical operation to combine two different signals and produce a new one.
Visit the next recommended links if you want to continue an in-depth reading on the convolution integral and the applications of convolution.
Convolution integral definition
A convolution integral is defined as:
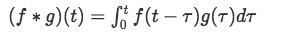
Where f and g are both functions of t on the left hand side, and one of them has been shifted in the right hand side (as we will explain below, it doesn't matter which one has been shifted). Remember that for a function to be shifted it means that it has algebraically passed through either horizontal translations or a vertical translations. You can also think on the definition of shifted functions as the one we saw on the step functions lessons where the unit step function has a value of 1.
As it can be seen in equation 1, the convolution definition can be summarized in that, to convolve a set of functions, one will be computing the integral of the product of such functions after one of them has been shifted through a horizontal translation. What we see on the right hand side of equation 1, is what we call a convolution integral.
There are many convolution properties which facilitate our calculations, one of the most useful characteristics is that due geometrical symmetry, the order in which the functions f(t) and g(t) are convolved in the operation does not affect the result, and so:
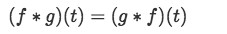
Evaluating an integral for convolution, we can translate this property into:
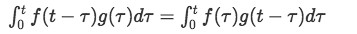
When trying to solve complicated inverse Laplace transforms that would be either impossible or very impractical to go through with techniques seen over our past lessons, we could just work with the characteristics of the convolution integral method shown in equations 2 and 3. Then, while working with differential equations, a third property we will talk about on this lesson comes in very handy: The Laplace transform of a convolution integral is equal to the product of the Laplace transform of two functions, these two functions corresponding to the ones being convolved (or f(t) and g(t) for simplicity).
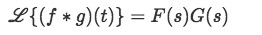
Thus, in order to work through the inverse Laplace transform of a complicated expression, we could very well separate this original expression into the product of two functions, each of these functions would be F(s) and G(s) you see in equation 4. As you can see, these F(s) and G(s) represent the Laplace transforms of the functions f(t) and g(t) respectively (since by definition: and ). And intuitively, we know that each of them will be simpler to solve their inverse Laplace transform to produce f and g, than directly calculating the inverse transformation of the original bigger expression.
By obtaining the inverse Laplace transform of F(s) and G(s), we will obtain f(t) and g(t) respectively, and then we just convolute these two functions together. The convolution produces a result equal to the inverse Laplace transform of the initial big mathematical expression.
Do not worry if this process looks confusing at this time, we will be working on a simple convolution example in the last section of this lesson.
Convolution integral example problems
Example 1
Solve the following convolution if and
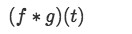
The equation right above tells us that since we are given this order in which the functions will be convolving on the operation, it means f(t) is the first one and has to be shifted. Using equation 1, we know "shifting" f(t), means for us to put this function in terms of t- instead of just t. From equation 1 we can also observe how g(t) has to be put in terms of . And so, our resulting convolution integral formula is:
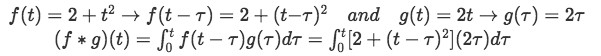
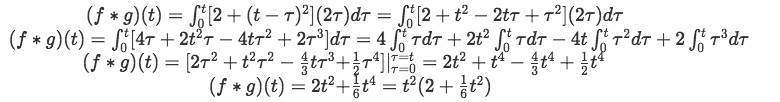
And we have solved our first convolution problem! Now, let us have some more fun with this problem and use it prove equations 2 and 3 with the same functions and .
Thus, solve the convolution:
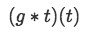
Just as before, let us shift the appropriate function and change the variable in the other one to form our convolution formula:
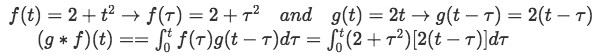
Now just convolute:
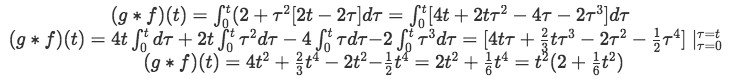
As you can see, the order in which a function convolutes with respect to other does not matter! And so, equations 2 and 3, have been proved.
But this lesson is not all about how to evaluate integrals for convolutions, the point which we are truly interested, and that will serve us to solve differential equations when needing the inverse Laplace transform of complicated functions, is the one illustrated in the next example:
Example 2
Find the inverse Laplace transform of the following function using convolution integrals:
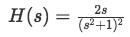
Remember equation 4, and notice that we have to separate the function into two factors, and so:
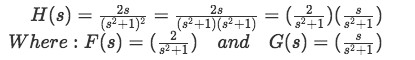
Having found F(s) and G(s) is time for us to obtain the inverse Laplace transform of each of these functions in order to find f(t) and g(t). For that, we look at our Laplace transform table:

And so, we compute the inverse Laplace transform of F(s) and G(s) by the method of table comparison. You can quickly observe that we will be using equations D and E due to the shape F and G have, thus:
- Using equation D, we solve the inverse Laplace transform of F(s) by noting a=1, therefore:
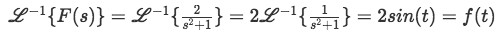
Equation for example 2(b): Inverse Laplace transform of F(s) - Using equation E, we solve the inverse Laplace transform of G(s), where a=1 again.
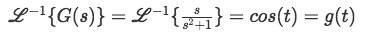
Equation for example 2(c): Inverse Laplace transform of G(s)
Our last step is to colvolute! Finding the convolution integral:
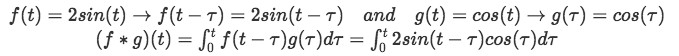
Using the next set of trigonometric identities we will simplify our convolution integral:
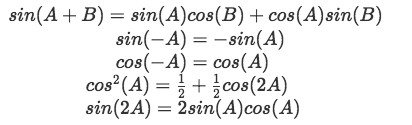
Setting A = t, B = -:
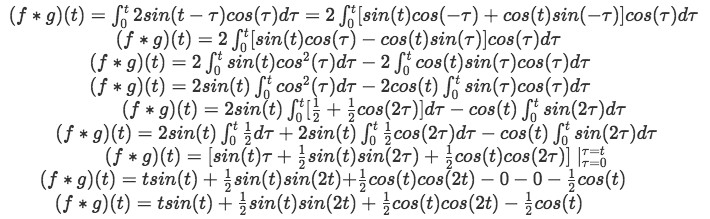
At this point, we need some more trigonometric equations to continue simplifying the result of the convolution integral, and so let us use:
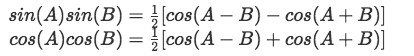
With the aid of these identities, we simplify the second and third term on the right hand side of the convolution result equation:
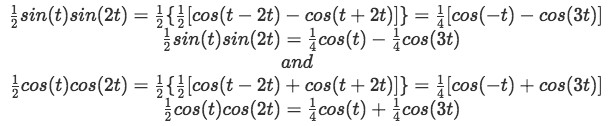
Now we can rewrite the convolution integral result:
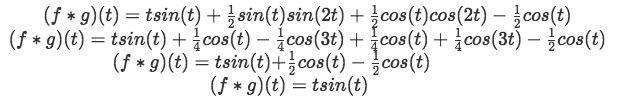
Therefore, the inverse Laplace transform of H(s) is:
For an extra example on finding the inverse Laplace transform using the convoluted definition seen through this lesson, you can visit these notes on convolution integrals.
A convolution integral is defined as:
Where , and are both functions.
Note that
Or,
Laplace Transforms of Convolution Integrals:






