Estimating Derivatives from a table

Estimating Derivatives from a table

Basic concepts: Definition of derivative ,

Lessons

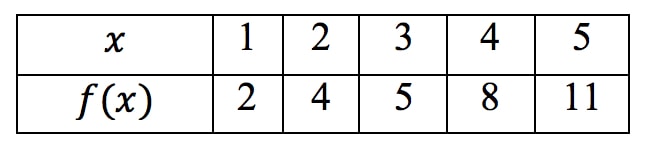
Recall when finding the slope of two points, we use the formula

m=y2−y1x2−x1m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}

Since the slope is the derivative, we can actually use this formula to estimate derivatives from a table.

We will just readjust the slope formula to look like this:

f′(a)≈f(a+h)−f(a)hf'(a) \approx \frac{f(a+h) - f(a)}{h}

Use this when estimating the slope of the very first point of the table

f′(a)≈f(a+h)−f(a−h)2hf'(a) \approx \frac{f(a+h) - f(a-h)}{2h}

Use this when estimating the slope of middle points of the table

f′(a)≈f(a)−f(a−h)hf'(a) \approx \frac{f(a) - f(a-h)}{h}

Use this when estimating the slope of the very last point of the table

Note that we will not use these formulas in the videos. We will just use the simple slope formula.

  • Introduction
    Estimating Derivatives from a table Overview:
  • 1.
    Estimating Derivatives

    Use the table below to estimate the following derivatives as accurately as possible:

    Estimate Derivative from a table
    a)
    f′(1)f'(1)

    b)
    f′(3)f'(3)

    c)
    f′(5)f'(5)

  • 2.
    Use the table below to estimate the following derivatives as accurately as possible:

    Estimate Derivative from a table

    a)
    f′(2)f'(2)

    b)
    f′(6)f'(6)

    c)
    f′(10)f'(10)

Do better in math today
Get Started Now
2.
Differentiation
2.1
Definition of derivative
2.2
Estimating derivatives from a table
2.3
Power rule
2.4
Slope and equation of tangent line
2.5
Chain rule
2.6
Derivative of trigonometric functions
2.7
Derivative of exponential functions
2.8
Product rule
2.9
Quotient rule
2.10
Implicit differentiation
2.11
Derivative of inverse trigonometric functions
2.12
Derivative of logarithmic functions
2.13
Higher order derivatives
Calculus 1