Trigonometric Substitution
Not all integrals can be solved by using u-substitution. For example let's say we want to integrate
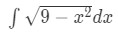
Are we able to use u-substitution here? Well let us set
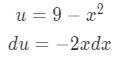
If we are to substitute this, our integral will become:
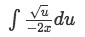
As you can see, this is a problem because our integral is not all in terms of u. So you would probably have to try something else. However no matter how hard you try, it will never work and u-substitution fails. This seems to be the case for a lot of functions with square roots. This is why we introduce a new method called trig-substitution. Trig substitutions help us integrate functions with square roots in them.
Trig Substitution Rules
As explained earlier, we want to use trigonometric substitution when we integrate functions with square roots. However, there are many different cases of square root functions. So how exactly do we know what type of trig we use as a substitution? Well here are 3 types you will most likely encounter, and these are the substitutions you would use:

where a is a constant.
How to do trig substitution
The reason why we use these substitutions for each case is because they make use of the following trig identities:
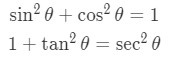
For example in case 1, using the substitution gives:
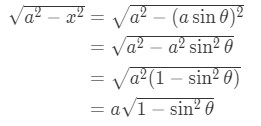
Using the identity
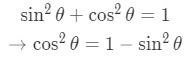
We get
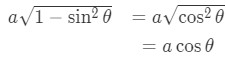
We can see that the substitution cleans up the function really well here, and can be easily integrated.
Similarly in case 2:
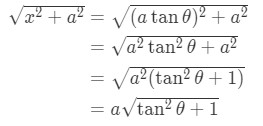
Now using the identity:
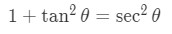
We have:

Again, the function is cleaned up and this can be easily integrated. Lastly in case 3,

Using the trig identity,
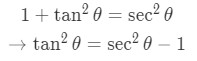
We now have
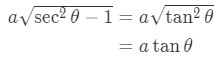
If this was an integral, then we would find the integral of tangent with coefficient a to find the answer.
Now in all cases, make sure to also find the derivative of the substitution because you are also going to substitute dx. So
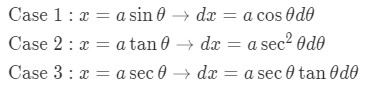
In summary, here is a trig-substitution table that shows you the strategy in using trig-substitution.
Trig Substitution Table

Trigonometric substitution integrals
Let's start by finding the integral of . In other words,
Question 1: Integrate
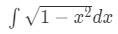
- Where do we start here? Let's rewrite the integral to

Equation 5: Trig Substitution with sin pt.2 - Notice that this looks really similar to , except . So that means we need to use the substitution . So we set:
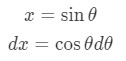
Equation 5: Trig Substitution with sin pt.3 - So substituting gives:
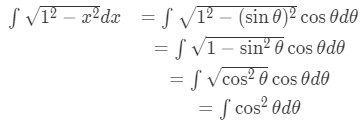
Equation 5: Trig Substitution with sin pt.4 - Now this is just an integral of a trig function. Notice that we need to use the identity:
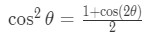
Equation 5: Trig Substitution with sin pt.5 - We are going to integrate that. This is one of the famous trig identities integrals you have probably done before. So our trig integrals become:

Equation 5: Trig Substitution with sin pt.6 - We may have finished integrating this trig function, but we are not done yet. Notice that our original integral was in terms of , so we have to make sure our answer is in terms of as well. We need to know how to convert , and in terms of . See that earlier our substitution was

Equation 5: Trig Substitution with sin pt.7 - Isolating for gives:
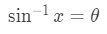
Equation 5: Trig Substitution with sin pt.8 - However, what is exactly? Well notice that:

Equation 5: Trig Substitution with sin pt.9 - We can use this to draw a triangle where the opposite length is and hypotenuse is .
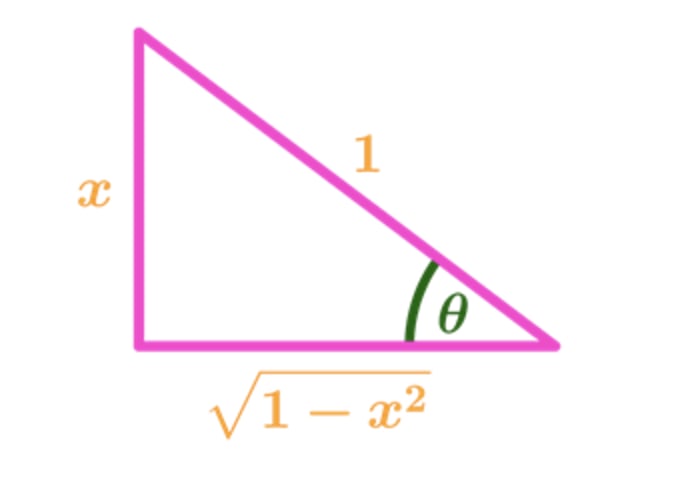
Graph 1: Trig Substitution Triangle with sin - Notice that the length of the adjacent is:
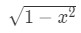
Equation 5: Trig Substitution with sin pt.10 - In addition, we know that
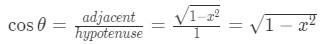
Equation 5: Trig Substitution with sin pt.11 - Hence substituting our answer back in terms of gives:
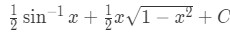
Equation 5: Trig Substitution with sin pt.12 which is answer for the integral of . Now let's look at another question similar to this.
Question 2: Integrate . In other words, integrate
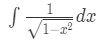
- This is very similar to the integral in question 1, but now the square root actually appears in the denominator. Now this question is actually pretty easy if you know about the integrals of inverse trig functions. Recall that:
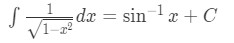
Equation 6: Trig Substitution of inverse sin pt.2 - So right away, you would know what the answer is. However, what if you don't spot this right away? Well, you can still use trigonometric substitution to obtain this answer! Notice from the denominator that:
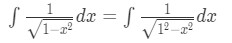
Equation 6: Trig Substitution of inverse sin pt.3 - Again, the denominator is in the form , except . So that means we need to use the substitution . So we set:
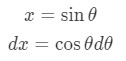
Equation 6: Trig Substitution of inverse sin pt.4 - Remember we also need to use the trigonometric identity:
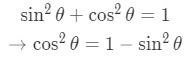
Equation 6: Trig Substitution of inverse sin pt.5 - So substituting gives:
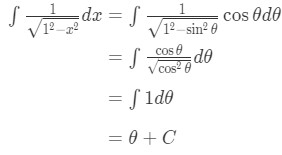
Equation 6: Trig Substitution of inverse sin pt.6 - Notice that
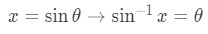
Equation 6: Trig Substitution of inverse sin pt.7 - So converting the answer back in terms of gives:
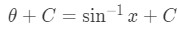
Equation 6: Trig Substitution of inverse sin pt.8 which matches the answer above. Now don't we try to do another similar question like this?
Question 3: Integrate
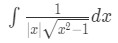
- Now again, these are one of those inverse trig integrals where:

Equation 7: Trig Substitution of inverse sec pt.2 - However, what if I did not know that in the first place? Again, use trigonometric substitution! First we are going to get rid of the absolute value and set a restriction for ourselves.
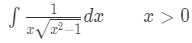
Equation 7: Trig Substitution of inverse sec pt.3 - Note that the square root in the denominator is in the form , except . So we use the substitution

Equation 7: Trig Substitution of inverse sec pt.4 - In addition we will use the trigonometric identity:
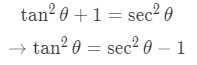
Equation 7: Trig Substitution of inverse sec pt.5 - So substituting gives us:
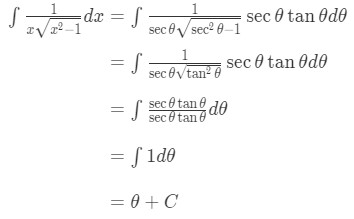
Equation 7: Trig Substitution of inverse sec pt.6 - Now remember we have to convert back in terms of . Notice from substitution earlier
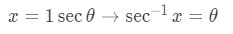
Equation 7: Trig Substitution of inverse sec pt.7 - So our final answer becomes:

Equation 7: Trig Substitution of inverse sec pt.8 which again is the exact answer as the above. Let's now do some harder ones that require to use the triangle to convert back in terms of again.
Question 4: Integrate
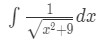
- Notice in the denominator that it is in the form , except . So that means we need to use the substitution . We set:
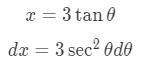
Equation 8: Trig Substitution with 3tan pt.2 - Remember we also need to use the trigonometric identity:
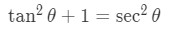
Equation 8: Trig Substitution with 3tan pt.3 - So substituting gives:
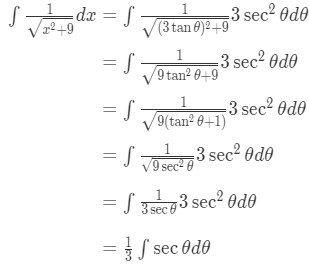
Equation 8: Trig Substitution with 3tan pt.4 - Again, this is just an integral of trig function. We know the integral of is . So

Equation 8: Trig Substitution with 3tan pt.5 - Remember that we need to convert back in terms of . So we need to find what how to express in terms of . Know that:

Equation 8: Trig Substitution with 3tan pt.6 - Drawing the triangle we see that:
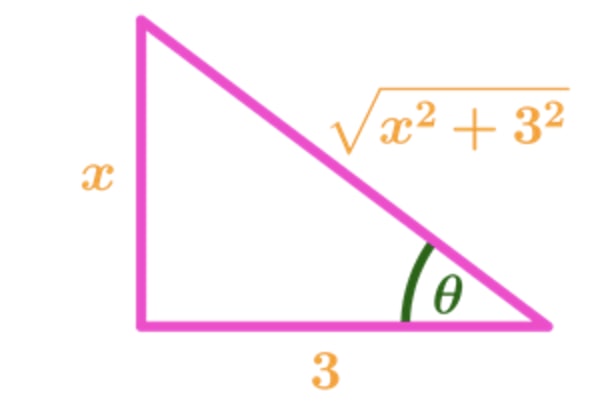
Graph 2: Trig Substitution Triangle with 3tan - This means
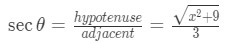
Equation 8: Trig Substitution with 3tan pt.7 - So our final answer is
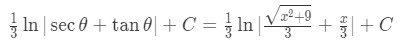
Equation 8: Trig Substitution with 3tan pt.8
Let's look at a slightly harder question that requires us to use case 3 of trigonometric substitution rule.
Question 5: Integrate
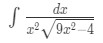
- First we need to play around the inside of the square root. Notice that:
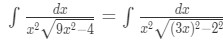
Equation 9: Trig Substitution with 2/3sec pt.2 - Note the square root in the denominator is in the form , except and →. So we use the substitution
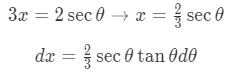
Equation 9: Trig Substitution with 2/3sec pt.3 - In addition we will use the trigonometric identity:
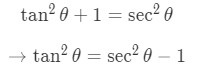
Equation 9: Trig Substitution with 2/3sec pt.4 - So substituting gives us:
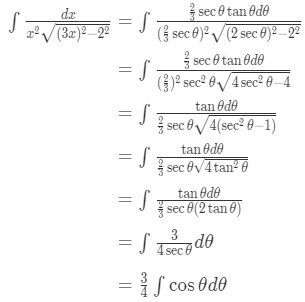
Equation 9: Trig Substitution with 2/3sec pt.5 - Again, this is just an integral of a trig function. So,
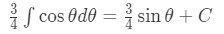
Equation 9: Trig Substitution with 2/3sec pt.6 - Now we need to figure out how to convert back in terms of . Notice that:
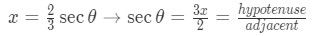
Equation 9: Trig Substitution with 2/3sec pt.7 - So drawing the triangle to find the opposite gives us:

Graph 3: Trig Substitution Triangle with 2/3sec - Notice that:
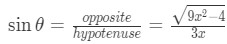
Equation 9: Trig Substitution with 2/3sec pt.8 - Hence our final answer gives us that:
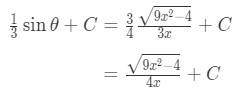
Equation 9: Trig Substitution with 2/3sec pt.9
If you would like to do more trig substitution integrals, I suggest you look at this link.
http://tutorial.math.lamar.edu/Classes/CalcII/TrigSubstitutions.aspx
There are a lot more integral substitution questions here, and Paul Lamar gives a step-by step solution each question! Have fun with trig substitution integration!






