Multiplication strategies
Topic Notes
In this lesson, we will learn:
- Understanding multiplication using arrays
- Representing a product as either: (1) a smaller product and a sum, or (2) a bigger product and a difference
- Tips and tricks for memorizing the 9 × multiplication table facts
Notes:
- Multiplication is just repeated addition

- Multiplication facts can be shown in an array model with circles/dots
- Using the array model, it shows that multiplication facts can be broken into groups of smaller multiplication facts:
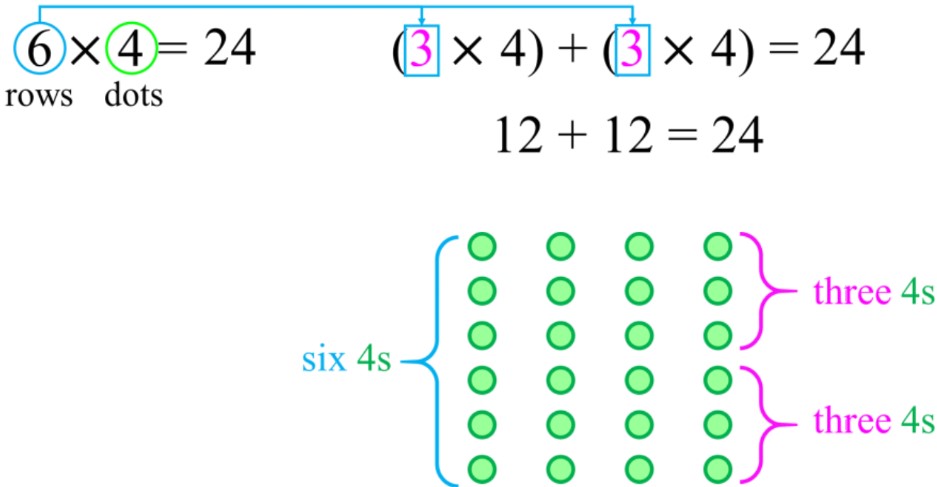
- Using the same array model, we can find the next multiplication fact by adding another row:

- Therefore, a product can be found as a smaller product and a sum

- Or, it could be found as a bigger product and a difference
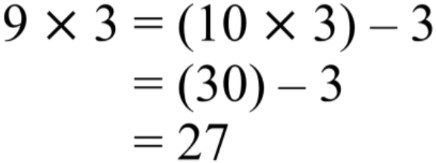
- The 9 × multiplication tables can be memorized using your fingers!
- Notice that the first ten multiples of 9 are mirrored after the 5-digit in 45
- Ex. 9, 18, 27, 36, 45 54, 63, 72, 81, 90
Introduction: Multiplication Strategies
Multiplication strategies are essential tools for students to master basic arithmetic skills. Our introduction video serves as a crucial starting point, offering a visual and engaging way to present these strategies. It demonstrates how to approach multiplication problems efficiently and confidently. One key strategy highlighted is the use of arrays, which help students visualize multiplication as groups of equal-sized sets. This concrete representation aids in understanding the concept of multiplication as repeated addition. Additionally, the video emphasizes the importance of breaking down multiplication facts into smaller, more manageable parts. This approach allows students to build on their existing knowledge and tackle more complex problems. By understanding these fundamental strategies, students can develop a strong foundation in multiplication, leading to improved mathematical skills overall. The video also introduces various other techniques, ensuring a comprehensive overview of multiplication strategies that cater to different learning styles and abilities.
Understanding Multiplication Using Arrays
Arrays are powerful visual tools that help students grasp the concept of multiplication. By arranging objects or dots in rows and columns, arrays provide a concrete representation of multiplication facts, making it easier for learners to understand and remember these essential mathematical relationships.
An array is a rectangular arrangement of objects or symbols, typically organized in equal rows and columns. In the context of multiplication, each row represents one group, and the number of items in each row represents the size of that group. For example, an array with 3 rows and 4 columns (3 x 4) would have 12 total objects, illustrating the multiplication fact 3 x 4 = 12.
Let's explore some examples to better understand how arrays represent multiplication facts:
- 2 x 3 array: Two rows with three objects in each row, totaling 6 objects
- 4 x 5 array: Four rows with five objects in each row, totaling 20 objects
- 6 x 2 array: Six rows with two objects in each row, totaling 12 objects
One of the most significant advantages of using arrays is their ability to visually demonstrate the commutative property of multiplication. This property states that the order of factors in multiplication doesn't affect the product. For instance, 3 x 4 and 4 x 3 both equal 12, despite having different arrangements.
Using arrays, we can easily visualize this concept:
- A 3 x 4 array (3 rows, 4 columns) has the same number of objects as a 4 x 3 array (4 rows, 3 columns)
- Both arrays contain 12 objects, demonstrating that 3 x 4 = 4 x 3 = 12
This visual representation helps students understand that changing the order of factors doesn't change the result, reinforcing the commutative property of multiplication.
Breaking Down Larger Multiplication Problems
Arrays are particularly useful when dealing with larger multiplication problems. They allow students to break down complex calculations into smaller, more manageable parts. This approach, known as the area model or array model, is especially helpful for multi-digit multiplication.
For example, let's consider the multiplication problem 14 x 23:
- Create an array with 14 rows and 23 columns
- Divide the array into smaller sections: 10 x 20, 10 x 3, 4 x 20, and 4 x 3
- Calculate each section separately: 200, 30, 80, and 12
- Add the results: 200 + 30 + 80 + 12 = 322
This method allows students to work with smaller, more familiar multiplication facts while solving a larger problem. It also provides a visual representation of how the distributive property works in multiplication.
Arrays offer several benefits in teaching and learning multiplication:
- Visual representation of abstract concepts
- Concrete model for understanding multiplication facts
- Clear illustration of the commutative property
- Tool for breaking down complex problems
- Foundation for understanding area and the distributive property
By incorporating arrays into multiplication lessons, educators can help students develop a deeper understanding of this fundamental mathematical operation. The visual nature of arrays makes multiplication more accessible and less intimidating, particularly for visual learners. As students progress, they can use their understanding of arrays to tackle more advanced concepts in mathematics, such as area, volume, and algebraic thinking.
Breaking Down Multiplication Facts
Breaking down multiplication facts is a powerful strategy that can significantly enhance your mental math skills and make complex calculations more manageable. This method involves splitting larger multiplication problems into smaller, more easily solvable parts. By mastering this technique, you can tackle a wide range of multiplication problems quickly and efficiently.
Let's start with a simple example: 6 x 4. Instead of memorizing this fact, we can break it down into two smaller, more familiar multiplications. We know that 6 is equal to 3 + 3, so we can rewrite the problem as (3 x 4) + (3 x 4). Most people find it easier to calculate 3 x 4, which equals 12. Now, we simply add 12 + 12 to get our final answer of 24.
This strategy becomes even more valuable when dealing with larger numbers. Consider the multiplication 15 x 8. At first glance, this might seem daunting, but we can break it down into more manageable parts. We know that 15 = 10 + 5, so we can rewrite the problem as (10 x 8) + (5 x 8).
Now, let's solve each part:
- 10 x 8 = 80 (This is usually an easy fact to remember)
- 5 x 8 = 40 (Half of 10 x 8, or you can think of it as 8 x 5 = 40)
Adding these results together, we get 80 + 40 = 120. Thus, 15 x 8 = 120.
The beauty of this method lies in its flexibility. You can choose how to break down the numbers based on what's easiest for you. For instance, you could also solve 15 x 8 by thinking of it as (15 x 10) - (15 x 2):
- 15 x 10 = 150 (Simply add a zero to 15)
- 15 x 2 = 30 (Double 15)
- 150 - 30 = 120
This strategy is particularly useful for mental math and quick calculations. By breaking down complex multiplication problems into smaller, more manageable parts, you can solve them more quickly and with less chance of error. It also helps in developing a deeper understanding of number relationships and properties of multiplication.
As you practice this method, you'll find that you can apply it to increasingly complex problems. For example, 23 x 7 could be broken down as (20 x 7) + (3 x 7), or even (25 x 7) - (2 x 7). The key is to find the breakdown that works best for you in each situation.
Breaking down multiplication facts also aids in estimating and checking your work. If you're multiplying 18 x 7, you might quickly estimate it as close to 20 x 7 = 140, giving you a ballpark figure to verify your detailed calculation.
To further enhance your skills with this strategy, try the following exercises:
- Practice breaking down multiplication facts for numbers between 11 and 20.
- Challenge yourself with two-digit by one-digit multiplications.
- Experiment with different ways of breaking down the same problem to find what works best for you.
Remember, the goal is not just to get the right answer, but to develop a flexible approach to multiplication that you can apply in various situations. With practice, you'll find that this method becomes second nature, allowing you to perform complex calculations quickly and accurately in your head.
Additionally, understanding the properties of multiplication can further enhance your ability to break down and solve multiplication problems efficiently.
Finding Products as Smaller Products and Sums
One effective strategy for mental calculations and improving multiplication skills is finding a product by using a smaller product and adding a sum. This method leverages our existing knowledge of simpler multiplication facts to solve more complex problems quickly and efficiently. By breaking down larger multiplication problems into smaller, more manageable parts, we can enhance our mental math abilities and solve problems with greater ease.
Let's explore this concept with a simple example: finding the product of 7 x 4. Instead of calculating this directly, we can use the smaller product of 6 x 4 (which equals 24) and then add 4 to it. Here's how it works:
- Start with 6 x 4 = 24
- Add 4 to 24
- The result is 28, which is indeed 7 x 4
This method works because 7 x 4 is essentially (6 + 1) x 4, which can be broken down into (6 x 4) + (1 x 4). By using this strategy, we're able to rely on our knowledge of easier multiplication facts and simple addition to solve more challenging problems.
This technique can be applied to various multiplication problems. For instance, let's consider 9 x 7:
- Start with 8 x 7 = 56 (a smaller, easier product)
- Add 7 to 56
- The result is 63, which is 9 x 7
The benefits of this method in mental calculations are numerous. Firstly, it allows us to break down complex problems into simpler, more manageable parts. This can reduce anxiety associated with larger numbers and make the calculation process less daunting. Secondly, it reinforces our understanding of number relationships and properties of multiplication, such as the distributive property.
Moreover, this strategy is particularly useful when dealing with numbers just above multiples of 10. For example, to calculate 11 x 12, we can use:
- 10 x 12 = 120 (an easy multiple of 10)
- Add 12 to 120
- The result is 132, which is 11 x 12
This method can also be extended to larger numbers. For instance, to find 23 x 4, we could use:
- 20 x 4 = 80
- Add 3 x 4 = 12
- The result is 92, which is 23 x 4
By practicing this technique, students and adults alike can improve their mental math skills and develop a deeper understanding of number relationships. It encourages flexible thinking about numbers and operations, which is a crucial skill in mathematics.
In conclusion, finding products by using smaller products and adding sums is a powerful strategy for mental calculations. It simplifies complex multiplication problems, builds on existing knowledge, and enhances overall mathematical fluency. By incorporating this method into regular practice, individuals can boost their confidence in mental math and approach multiplication problems with greater ease and efficiency.
Finding Products as Bigger Products and Differences
When it comes to mental math and quick calculations, one powerful strategy is finding a product by using a bigger product and subtracting a difference. This method is particularly useful for multiplication involving 9, but it can be applied to various other calculations as well. Let's explore this concept in detail and see how it can simplify our mental math processes.
The core idea behind this strategy is to leverage our familiarity with easier numbers, like multiples of 10, and then make a small adjustment to arrive at the desired result. For instance, let's consider the example of 9 x 3. Instead of directly calculating this, we can think of it as (10 x 3) - 3. Here's how it works:
1. 10 x 3 = 30 (an easy calculation to do mentally)
2. 30 - 3 = 27
Therefore, 9 x 3 = 27
This method is particularly effective for multiplication by 9 because 9 is just one less than 10, making the subtraction step straightforward. Let's look at a few more examples involving 9:
9 x 6 = (10 x 6) - 6 = 60 - 6 = 54
9 x 8 = (10 x 8) - 8 = 80 - 8 = 72
9 x 12 = (10 x 12) - 12 = 120 - 12 = 108
As you can see, this strategy allows us to quickly calculate products involving 9 by first multiplying by 10 (which is usually easier) and then subtracting the number we're multiplying by. This method can be especially helpful when dealing with larger numbers, where mental calculation might otherwise be challenging.
While this technique shines with multiplication by 9, it's not limited to just that. We can apply this strategy to other calculations as well. For example:
18 x 5 can be calculated as (20 x 5) - (2 x 5) = 100 - 10 = 90
24 x 3 can be thought of as (25 x 3) - (1 x 3) = 75 - 3 = 72
48 x 6 can be solved as (50 x 6) - (2 x 6) = 300 - 12 = 288
In each of these cases, we're using a nearby, easier-to-calculate number (like multiples of 10 or 25) and then adjusting for the difference. This approach not only simplifies mental calculations but also helps in developing a deeper understanding of number relationships and properties.
To further reinforce this concept, let's consider how we might apply this strategy to even larger numbers:
99 x 7 = (100 x 7) - 7 = 700 - 7 = 693
198 x 5 = (200 x 5) - (2 x 5) = 1000 - 10 = 990
895 x 3 = (900 x 3) - (5 x 3) = 2700 - 15 = 2685
By mastering this technique of finding products as bigger products and differences, you can significantly enhance your mental math abilities. It's a versatile strategy that can be adapted to various situations, making quick calculations easier and more intuitive. Practice with different numbers and scenarios to fully integrate this method into your mathematical toolkit.
Memorizing the 9 Times Table
Learning the 9 times table can be challenging for many students, but there's a fun and easy method that uses your fingers to help memorize these multiplication facts. This technique, known as the "finger method," is an excellent way to reinforce the patterns in the 9 times table and make learning more engaging.
The Finger Method for the 9 Times Table
Here's a step-by-step guide to using the finger method:
- Hold both hands in front of you with palms facing away.
- Number your fingers from left to right, starting with your left pinky as 1 and ending with your right pinky as 10.
- To multiply 9 by any number from 1 to 10, simply bend the finger corresponding to that number.
- The fingers to the left of the bent finger represent the tens digit, while the fingers to the right represent the ones digit.
Examples Using the Finger Method
Let's practice with a few examples:
- 9 x 3: Bend your third finger (left middle finger). You have 2 fingers to the left and 7 to the right, so the answer is 27.
- 9 x 7: Bend your seventh finger (right index finger). You have 6 fingers to the left and 3 to the right, so the answer is 63.
- 9 x 10: Bend your tenth finger (right pinky). You have 9 fingers to the left and 0 to the right, so the answer is 90.
Patterns in the 9 Times Table
The 9 times table has some interesting patterns that can help with memorization:
- The digits in each product always add up to 9. For example, in 9 x 7 = 63, 6 + 3 = 9.
- The tens digit increases by 1 each time, while the ones digit decreases by 1.
- The sum of the digits in the multiplicand and the product is always 9. For example, 9 x 5 = 45, and 5 + 4 = 9.
Practice Exercises
To reinforce this memorization technique, try these exercises:
- Use the finger method to calculate 9 x 4, 9 x 6, and 9 x 8.
- Without using your fingers, try to recall the products of 9 x 2, 9 x 5, and 9 x 9.
- Look for the patterns in these products: 18, 36, 54, 72, 90.
- Create a 9 times table chart and color-code the tens and ones digits to visualize the pattern.
Benefits of the Finger Method
The finger method for the 9 times table offers several advantages:
- It's a visual and kinesthetic approach, making it easier for many learners to remember.
- It reinforces the patterns in the 9 times table, aiding in long-term memorization.
- It's always available you don't need any tools other than your hands.
- It builds confidence in math skills, especially for students who struggle with traditional memorization.
While the finger method is an excellent tool for learning the 9 times table, it's important to eventually transition to mental math. Use this technique as a stepping stone to help understand the patterns and relationships within the 9 times table. With practice, students will find that they can quickly recall these multiplication facts without
Conclusion: Mastering Multiplication Strategies
In this lesson, we explored essential multiplication strategies that form the foundation of mathematical proficiency. The introduction video provided a visual understanding of these concepts, making them more accessible and relatable. Key strategies discussed include the distributive property, breaking numbers apart, and using known facts to solve more complex problems. Regular practice of these techniques is crucial for developing fluency and confidence in multiplication. We encourage you to apply these strategies in various mathematical contexts, from everyday problem-solving to more advanced mathematical concepts. Remember, mastery comes with consistent practice and application. To further enhance your multiplication skills, we recommend engaging with additional exercises and resources available on our platform. Take the next step in your mathematical journey by exploring our interactive multiplication games and worksheets. By mastering these strategies, you'll build a strong foundation for future mathematical success.
Understanding the distributive property is particularly important as it allows you to simplify and solve equations more efficiently. This property is not only useful in multiplication but also in various algebraic contexts. By breaking down complex problems into simpler parts, you can tackle them with greater ease and accuracy. Make sure to practice regularly and seek out additional resources to reinforce your understanding of this key concept.
Understanding Products Using Smaller Products
Understanding products using smaller products
Turn the product into the sum of two smaller group products.
8 × 4 = (5 × 4) + ( __ × 4)
FAQs
-
What is the array method in multiplication?
The array method is a visual representation of multiplication using rows and columns. It helps students understand multiplication as repeated addition and visualize the commutative property. For example, a 3x4 array would have 3 rows and 4 columns, totaling 12 objects, illustrating that 3 x 4 = 12.
-
How can breaking down multiplication facts help in solving problems?
Breaking down multiplication facts involves splitting larger problems into smaller, more manageable parts. For instance, 15 x 8 can be broken down as (10 x 8) + (5 x 8). This strategy makes complex calculations easier, especially for mental math, and helps in understanding number relationships.
-
What is the finger method for the 9 times table?
The finger method is a technique where you use your fingers to calculate multiples of 9. Hold up both hands, number your fingers 1-10 from left to right, and bend the finger corresponding to the number you're multiplying by 9. The fingers to the left represent tens, and those to the right represent ones in the answer.
-
How can finding products as bigger products and differences help in multiplication?
This strategy involves using a nearby, easier-to-calculate number and then adjusting for the difference. For example, 9 x 7 can be calculated as (10 x 7) - 7 = 70 - 7 = 63. This method is particularly useful for mental math and quick calculations, especially with numbers close to multiples of 10.
-
Why is understanding the distributive property important in multiplication?
The distributive property allows you to break down complex multiplication problems into simpler parts. It states that a(b + c) = ab + ac. This property is crucial for mental math, algebraic thinking, and solving more advanced mathematical problems. It provides a foundation for understanding how multiplication works with larger numbers and variables.
Prerequisite Topics
Understanding the foundations of mathematics is crucial for mastering more advanced concepts. When it comes to multiplication strategies, one essential prerequisite topic stands out: properties of matrix multiplication. This fundamental concept plays a significant role in developing a comprehensive understanding of various multiplication techniques and their applications.
Multiplication strategies are not just about memorizing times tables; they involve a deeper comprehension of mathematical principles. The properties of multiplication form the backbone of these strategies, providing a solid framework for solving complex problems efficiently. By mastering these properties, students can approach multiplication tasks with confidence and flexibility.
One of the key reasons why understanding the properties of matrix multiplication is crucial is its application in advanced mathematics and real-world scenarios. These properties, such as associativity, distributivity, and commutativity, are not limited to simple arithmetic but extend to more complex mathematical structures like matrices. This knowledge becomes invaluable when dealing with multidimensional data, computer graphics, and various scientific computations.
Moreover, grasping the properties of matrix multiplication enhances problem-solving skills. It allows students to break down complex multiplication problems into simpler, more manageable parts. This decomposition is a fundamental strategy in mathematics and is particularly useful when dealing with large numbers or algebraic expressions.
The connection between properties of multiplication and various multiplication strategies is profound. For instance, the distributive property is the basis for many mental math techniques and algorithms used in multiplication. Understanding this property helps students quickly multiply numbers by breaking them down into more convenient parts.
Furthermore, these properties are not isolated concepts but are interconnected with other mathematical ideas. They form the foundation for understanding more advanced topics in algebra, calculus, and linear algebra. As students progress in their mathematical journey, they will find that a solid grasp of these fundamental properties makes learning new concepts much easier and more intuitive.
In conclusion, the importance of understanding prerequisite topics like the properties of matrix multiplication cannot be overstated when it comes to mastering multiplication strategies. This knowledge not only aids in solving immediate multiplication problems but also paves the way for understanding more complex mathematical concepts. By investing time in mastering these fundamental properties, students set themselves up for success in their mathematical studies and beyond.

