In this lesson, we will learn how to find a determinant of a 2 x 2 matrix. To find the determinant, we multiply the top left entry and bottom right entry and subtract it with the product of the top right entry and bottom left entry. We will use these determinants later on in the course to show if a matrix is invertible. We will also use it to find inverses of 2 x 2 matrices.
The determinant of a 2x2 matrix
What is the determinant of a matrix
In order to define what is a determinant of a matrix we need to go back a to our definition of a matrix. Remember that we have learnt that a matrix is an ordered list of numbers put in a rectangular bracket. This list can also be called a rectangular array, and it provides an orderly fashion to display a list of information elements. If you want to review the definition of the matrix with more detail you can revisit our lesson on notation of matrices.A matrix describes a linear transformation or linear map, which is a kind of transcription between two types of algebraic structures, such as vector fields. In that way, we can resolve systems of linear equations by representing a linear system as a matrix. The matrix representation of a linear system is made by using all of the variable coefficients found in the system, and use them as element entries to construct the rectangular array of an appropriate size augmented matrix. In such matrix, the results of each equation from the system will be placed on the right hand side of the vertical line which represents the equal sign.
You may be asking yourself, what about the definition of the determinant of a matrix then? Knowing that a matrix is an array containing the information of a linear transformation, and that this array can be conformed by the coefficients of each variable in an equation system, we can describe the function of a determinant: a determinant will scale the linear transformation from the matrix, it will allow us to obtain the inverse of the matrix (if there is one) and it will aid in the solution of systems of linear equations by producing conditions in which we can expect certain results or characteristics from the system (depending on the determinant and the type of linear system, we can know if we may expect a unique solution, more than one solution or none at all for the system).
But there is a condition to obtain a matrix determinant, the matrix must be a square matrix in order to calculate it. Hence, the simplified definition is that the determinant of nxn matrix is a value that can be computed from a square matrix to aid in the resolution of linear equation systems associated with such matrix. The determinant of a non square matrix does not exist, only determinants of square matrices are defined mathematically.
The determinant of a matrix can be denoted simply as det , det() or . This last notation comes from the notation we directly apply to the matrix we are obtaining the determinant of. In other words, we usually write down matrices and their determinants in a very similar way:

But notice, when we write down the matrix we have two brackets that are closed inwards, and when we are referring to the determinant of the matrix, the matrix components are surrounded by two straight lines.
We will talk more about this topic on a later lesson dedicated to the properties of determinants , still, we will introduce a few of these properties quickly today today so you can have a better idea on how to find the determinant of a 2x2 matrix and why is this important.
How to find the determinant of a matrix
The computation of the determinant of a matrix varies depending on the dimensions of the matrix itself, as the dimensions of the matrix increase, the determinant calculation gets extensive and more complicated.On this lesson we will focus on the calculation of determinants from 2x2 square matrices only, we will study the steps to obtain the determinant of a 3x3 matrix (General & Shortcut method) in a later lesson.
How do you find the determinant of a 2x2 matrix
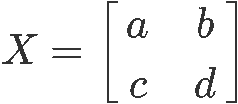
Its determinant is mathematically defined to be:
Which can also be written as:

The only simpler determinant to obtain besides the determinant of a 2x2 matrix is the determinant of 1x1 matrix which is defined to be equal to the only element inside the matrix.
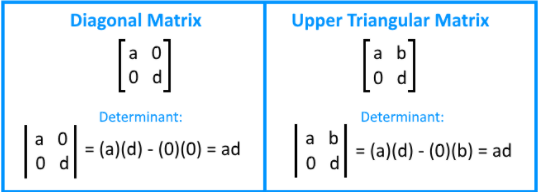
Determinant of triangular matrix
An upper triangular matrix is a square matrix in row echelon form in which all of the pivots are in consecutive columns producing the main diagonal, thus resulting in a triangle made out of zeros below the main diagonal in the left bottom corner. A lower triangular matrix has the positions of the zeros in opposite position from the upper triangular matrix, therefore, a lower triangular matrix is that where the zeros are found above the main diagonal to the upper right corner.

Given that only the upper triangular matrix is in echelon form, which is essential when solving systems of linear equations through matrices and row operations, that is the triangular matrix which we are interested in.
It so happens that the determinant of an upper triangular matrix is the result from the multiplication of all of the elements found in its diagonal, no matter the order (size) of the matrix. Therefore, when row reducing a square matrix formed by a system of linear equations, if you arrive to an echelon form that is equal to an upper triangular matrix, you can easily compute its determinant and through that, obtain information about the kind of solutions to be expected from the system.
Determinant of a diagonal matrix
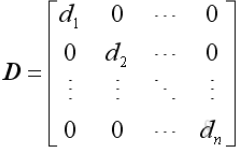
In general, the determinant of a diagonal matrix is equal to the product of the entries on its diagonal. If we think of determinant found in equation 2 as a diagonal matrix, that means that the elements and are equal to zero, therefore, we can prove that the determinant of such diagonal matrix would be the result of multiplying the entries on the matrix diagonal by following equation 3 to calculate it. The result of calculating the 2x2 matrix determinant of in this case would be equal to (a)(d)-(0)(0)=ad, which is simply, multiplying the diagonal elements.
Notice that to obtain the determinant of a triangular matrix and a diagonal matrix we can use the same simple approach. If you think about it, this comes from the fact that in a diagonal matrix, all of the components above and below the diagonal are zeros, thus if we follow the formula for the determinant of a 2x2 matrix shown in equation 3, we will see that the second term in the formula is a multiplication of two zeros giving a zero to subtract from those elements n the diagonal and thus leaving them as the only result. Something very similar happens in triangular matrices, but instead of having a multiplication of two zeros in the second term of the determinant formula, you have the multiplication of a zero and a non-zero value, which still results in zero and leaves the first multiplication as result.
Confusing? Take a look at the next equations for each of the cases mentioned:
Determinant of symmetric matrix
We obtain the transpose of a matrix by rearranging the columns of the original matrix as rows in the transpose. For the case of square matrices, the transpose matrix will remain to be the same order since it will continue to have the same amount of rows and columns than the original.
The process of obtaining the transpose of a matrix can be seen in the next equation:

For the case of a third degree square matrix, the transpose can be obtained in the same way, just as seen below:

As you can see, if symmetric matrix means a given matrix is equal to its transpose, it also means the symmetry, which comes from respect to the diagonal of the matrices, will allow all the elements inside the matrix to remain equal. And so, the determinant of a symmetric matrix, no matter its size, is calculated using the same process as with any other square matrices, but there is a special case: all diagonal matrices are also, symmetric matrices, and so, their determinants can be calculated just by multiplying its diagonal elements.
Matrix determinant properties
Besides finding the determinant of a matrix, there are interesting characteristics and conditions associated with this value (the determinant result) that provide useful information about operations and processes that can be calculated with matrices, such as matrix inversion, diagonalization and the effect of certain row operations on the determinant results (which at the same time, may or may not affect invertibility, etcThe interesting characteristics and conditions coming from finding the determinant of a 2x2 matrix (or any other square matrix of higher order for that matter) are what we call properties of the result. Although such properties will be covered in detail in a later lesson (as mentioned earlier), let us give at least a brief explanation of them and the types of operations they are associated with in relation to the matrix.
The properties of determinants are categorized in three sections each depending to the type of matrix operations they are associated with:
- Row operation properties
- Multiplicative properties
- Other miscellaneous properties
Row operation properties of a 2x2 matrix determinant are associated, as their name suggests, to the three types of matrix row operations that can be performed while row reducing a matrix, and how they will affect the outcome of the determinant of the matrix.
The main three properties related to row operations are:
- If a multiple of one row of a given matrix is added to another row to produce a second matrix, which retains the same proportionality as the first, then the determinant of the original matrix is equal to the determinant of the second matrix obtained after the row operation.
- If two rows are interchanged in a matrix, the determinant of the original matrix is equal to the negative of the determinant of the resulting matrix after the row exchange.
- If a constant is multiplied to a row inside a given matrix which produces a different second matrix, the determinant of resulting matrix after the multiplication of the constant is equal to the determinant of the original matrix times the same constant.
The main multiplicative property determinants is probably that if you multiply two matrices and then obtain the determinant of the resulting one, this determinant value would be equal if you were to obtain the determinant of each matrix separately and then multiply them with each other. Simply said: .
Other miscellaneous properties talk about how the determinant of a matrix is equal to the determinant of its transpose, and one of the most important ones: that a matrix is invertible if, and only if, its determinant is NOT zero. This last property is of main importance for our next lesson where we will introduce matrix inversion.
Remember, all of the properties and rules we have seen today, although we have focused in 2x2 matrices, they do apply equally when finding the determinant of a large matrix. Also take into account all of the properties have been just briefly discussed as an introduction for this lesson, for extensive explanations on them please visit our lesson about properties of determinants, which comes later in our course.
Finding the determinant of a 2x2 matrix
Now that we have seen the general method of how to find the determinant of a 2x2 matrix and that we have seen different matrix cases and properties, is time for us to use the knowledge obtained and solve a few example exercises:Example exercises
1. We define the 2x2 matrix shown below as :
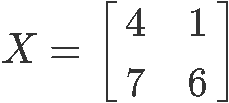
Find the determinant of matrix by following the equation for the determinant of a 2x2 matrix shown in the second section of this lesson:
2. Given the 2x2 matrix A as shown below
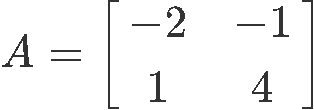
Find the determinant of 2x2 matrix :
3. Given the 2x2 matrix E as shown below
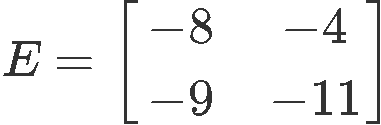
Evaluate the determinant of the matrix E:
4. Given the 2x2 matrix F as shown below
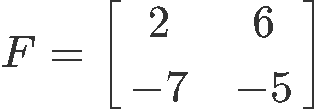
Find its determinant:
5. Given the 2x2 matrix Y as shown below
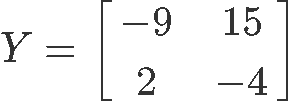
Find its determinant:
6. Given the 2x2 matrix Z as shown below
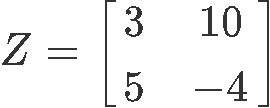
Find its determinant:
Look at the values obtained throughout all of the six exercises done above on the determinant of a 2x2 matrix, even for a small matrix of dimensions 2x2, these values are significant in finding if such matrices can, or cannot, be inverted. Our next section will be focused on this, the 2x2 invertible matrix, or in other words, how do we know if we can invert a matrix.
We hope this lesson has been useful and of your enjoyment, before we jump onto the next one let us give you a few recommendations so you can continue your studies on the topic of today. First, we recommend you to visit this brief lesson on determinants, where you will find an introduction to a higher order determinant at the end of it, and then you can take a look into this other lesson which covers both determinants and Cramer's rule. Finally, we would like to recommend this article on the the determinant of a square matrix which funnily enough, mentions at the beginning that the author has not been able to find a good English definition of what a determinant is (at least at the time he wrote the text). We hope this StudyPug lesson has been able to provide that for sure: a clear definition of the determinant of a square matrix (but if not, do not hesitate to ask!).
Well, this has been fun today, see you onto the next lesson!
Let the matrix 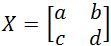 , where and are all numbers. We denote the determinant of to be det. To find the determinant of a 2 x 2 matrix we compute the following:
, where and are all numbers. We denote the determinant of to be det. To find the determinant of a 2 x 2 matrix we compute the following:
det
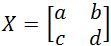 , where and are all numbers. We denote the determinant of to be det. To find the determinant of a 2 x 2 matrix we compute the following:
, where and are all numbers. We denote the determinant of to be det. To find the determinant of a 2 x 2 matrix we compute the following:det

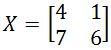 . Find the determinant.
. Find the determinant.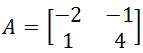 . Find the determinant.
. Find the determinant.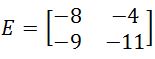 . Find the determinant.
. Find the determinant.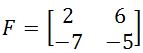 . Find the determinant.
. Find the determinant. . Find the determinant.
. Find the determinant.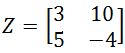 . Find the determinant.
. Find the determinant.




