2 x 2 invertible matrix
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
2x2 Invertible matrix
We are about to start a series of lessons dedicated to the inverses of matrices. The topic of today is to learn to identify those matrices which can be inverted and those which can't. On later lessons we will obtain the inverses of different size matrices and how to use them when solving systems of linear equations.
What is an invertible matrix
An invertible matrix, also called a nondegenerate matrix or a nonsingular matrix, is a type of square matrix containing real or complex numbers which is the most common in existence. Its main characteristic is that for an invertible matrix there is always another matrix which multiplied to the first, will produce the identity matrix of the same dimensions as them.
In other words, an invertible matrix is that which has an "inverse" matrix related to it, and if both of them are multiplied together (no matter in which order), the result will be an identity matrix of the same order. To explain this concept a little better let us define a 2x2 matrix (a square matrix of second order) called X. Then, X is said to be an invertible 2x2 matrix if and only if there is an inverse matrix X−1 which multiplied to X produces a 2x2 identity matrix as shown below:
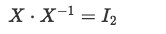
For clarity purposes, let us repeat that in this case the resultant identity matrix I2 is of second order since the matrices producing it are of second order too. In general, we know we can invert a matrix of nxn dimensions which we define as A if the following condition is met:

Keep always in mind that there is a difference between an "invertible matrix" and an "inverted matrix". And invertible matrix is any matrix which has the capacity of being inverted due to the type of determinant it has, while an inverted matrix is one which has already passed through the inversion process. If we look at equation 2, A would be referred as the invertible matrix and A−1 would be the inverted matrix.
Before we pass to the next section where we will learn how to tell if a matrix is invertible and when is a matrix not invertible, let us say something about a non invertible matrix: Remember that a matrix is a rectangular array of ordered coefficients, in other words, it can be taken as an array of information values. We have mentioned before that an invertible matrix is the most common case in existence, in this case we are talking about a continuous uniform distribution of arrays with information values; therefore the denomination of "nonsingular" matrix for a matrix invertible comes from the fact that in such distribution, a study case (a selected array from the distribution) would almost always come to be an invertible array or, invertible matrix. Therefore, a non invertible matrix is called a singular matrix, because is rare to find on an ideal distribution of information.
This last bit of information is essential when studying statistics and probability theory, and although for now we will keep our focus in linear algebra (the topic of this course), it is always important to understand the extent of mathematical concepts throughout different areas of study.
How to determine if a matrix is invertible
So after the introduction above we arrive to the main question of this lesson: When is a matrix invertible? If we define a nxn matrix we say that:
In later lessons we will talk about the invertible matrix theorem which gives a series of conditions equivalent to the statement above, that if met, define an invertible matrix.
- Is the zero matrix invertible?
Since a matrix is invertible when there is another matrix (its inverse) which multiplied with the first one produces an identity matrix of the same order, a zero matrix cannot be an invertible matrix. If you think about it, no matter which matrix you multiply to a zero matrix, and no matter the order in which the multiplication occurs, the result of such matrix multiplication will always be a zero matrix because all of the element entries in the zero matrix are zeros.

Equation 3: Matrix multiplication with a zero matrix Under the same logic, we can conclude a general rule: any square matrix which contains a complete row or a complete column filled with zeros, cannot be inverted since it cannot produce an identity matrix through matrix multiplication.
- Is the identity matrix invertible?
Yes, the identity matrix is invertible. We know what makes a matrix invertible is the fact that there is another matrix out there, which we call the inverse matrix of the original, which multiplied by the original produces the identity matrix as a result. This definition may sound confusing if the matrix we are trying to invert is the identity itself, but simply said, the inverse of the identity matrix is itself, and it can be shown below:
Multiplying an identity matrix by itself produces the identity matrix once more, and so, the invertible matrix definition is met, as can be seen in equation 8.
Equation 4: The identity matrix as inverse multiplicative of itself.
Such characteristic places the identity matrix into a group of special matrices called involutory matrices. Involution is the name given to functions which are their own inverses, in the case of linear algebra, an involutory matrix is that which multiplied by itself (squaring the matrix) produces the identity matrix, and so, following the concept from general mathematics, an involutory matrix is that which is its own inverse. The identity matrix itself is the main involutory matrix since all of the involutory matrices existent are square roots of it.
Invertible matrix properties
Besides the fact that there is an inverse matrix out there for an invertible matrix to be multiplied with and obtain the same order identity matrix out, you may be wondering: what does it mean for a matrix to be invertible?
The answer to this question is not simple, but the idea can be summed up by saying that an invertible matrix would allow us to manipulate the information contained in the rectangular array of a matrix in ways that may be convenient while trying to solve systems of linear equations or performing other matrix operations.
For that matter, we have made a list of some of the most important properties to remember about an invertible matrix, which may be useful to you in future lessons. In order to start this list, we need to define A as a square matrix of any order (with any dimensions), then, for A to be an invertible matrix, the next conditions must hold true:
- (A−1)−1=A
The inverse of a matrix is denoted as a the division of the unit by the matrix or the matrix with an exponent of -1. Thus, when inverting matrix A, the notation for its inverse is equal to A−1.
Having this in mind the expression above can be read as "the inverse of the inverse of A is equal to A" which makes sense and although it sounds redundant, it can be useful when a matrix needs to be inverted for a specific function, but then the original matrix is needed once more in an operation.
In simple words, this property says that if you invert matrix A, you will obtain A−1 (the inverse of A), and if you invert A−1 once more, you will obtain A back again. - (AT)−1=(A−1)T
The expression above affirms that it doesn't matter the order in which you invert the transpose of a matrix. In other words, you can obtain the transpose of the matrix and then invert the resulting matrix (as shown in the left hand side of the expression) or you can invert the given matrix and then obtain the transpose of the resulting inversion (as shown in the right hand side of the expression). Both processes will yield the exact same resulting matrix as long as you use the same matrix A to start with.
As a reminder, keep in mind the transpose of a matrix can be obtained by rearranging the columns of the original matrix as rows in the transpose. For the case of square matrices, the transpose matrix will remain to be the same order since it will continue to have the same amount of rows and columns than the original.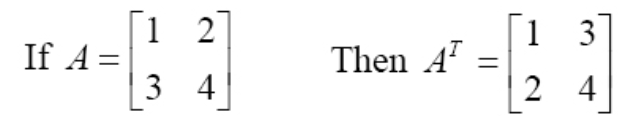
Equation 5: Obtaining the transpose of a 2x2 matrix - (kA)−1=k−1A−1 for non-zero scalar k
What we see on the expression above is the distributive property of an exponent, which works in the same way for a matrix notation. As mentioned before, the -1 exponent represents the inversion of the matrix; for this case, a matrix is multiplied to a constant coefficient and then the scalar multiplication result is inverted (elevated to the power of -1), this is equivalent to having done the matrix inversion first, and separately "invert" the scalar coefficient too (elevate it to the power of -1, same as dividing 1 by the coefficient) and then, perform the scalar multiplication between the inverted scalar and the inverted matrix.
Notice this has the clarification that k must be a non-zero scalar because a zero scalar would convert the whole expression into zero. - For any two square matrices A and B, (AB)−1=B−1A−1
Once again, this property describes the distributive nature of exponents when applied to a type of multiplication with matrices. If you take a look at the equation above, this is very similar to the expression shown on the third property, the only difference is that the third property shows a scalar multiplication inside the parenthesis on the left hand side of the equation, while the expression here (in property number four) contains a matrix multiplication inside the parenthesis on the left hand side of the equation.
In short, the expression for property number four says that the result of the multiplication of two matrices after they have been inverted is the same as multiplying the two original matrices first and then invert the resulting one. - det(A−1)=(detA)−1
In simple words, this property defines that the determinant of an inverted matrix is the same as obtaining the determinant of the original matrix and then "invert" this result by elevating it to the power of -1.
Proving a matrix is invertible
To finalize this lesson we will work on a few example exercises where we will be determining if a matrix is invertible. Notice we have not learned on this lesson how to invert a matrix, that will be explained in our next lesson named the inverse of a 2x2 matrix.
Example exercises
- Given the matrix X as shown below:
Is X an invertible matrix 2x2? Remember that the condition for a matrix to be invertible is that det(A)=0. And so, we obtain the determinant of matrix X:
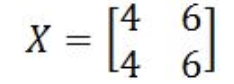
Equation 6: Matrix X The determinant of matrix X is equal to zero, therefore, this matrix is NOT invertible.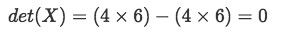
Equation 7: Determinant of matrix X - Given the matrix A as shown below:
Could we invert a 2x2 matrix such as A?
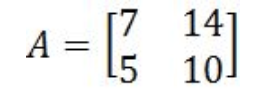
Equation 8: Matrix A The determinant of matrix A is equal to zero, therefore, this matrix is NOT invertible.
Equation 9: Determinant of matrix A - Given the 2x2 matrix E as shown below
Is E invertible?
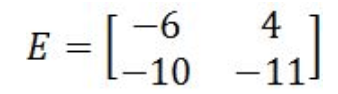
Equation 10: Matrix E Since the determinant is not zero, then matrix E is invertible.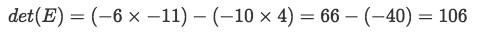
Equation 11: Determinant of matrix E - Given the 2x2 matrix F as shown below
Is inverting a 2x2 matrix such as F possible?
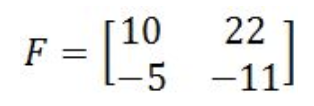
Equation 12: Matrix F The determinant of matrix F is equal to zero, therefore, this matrix is NOT invertible.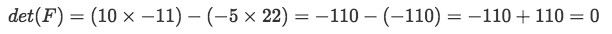
Equation 13: Determinant of matrix F - Given the 2x2 matrix Y as shown below
Is matrix Y invertible?
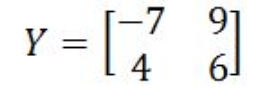
Equation 14: Matrix Y Since the determinant is not zero, then matrix Y is invertible.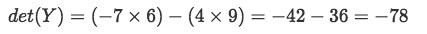
Equation 15: Determinant of matrix Y - Given the 2x2 matrix Z as shown below
Is matrix Z invertible?
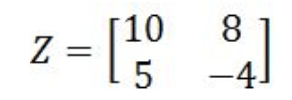
Equation 16: Matrix Z Since the determinant is not zero, then matrix Z is invertible.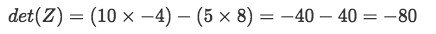
Equation 17: Determinant of matrix Z
After learning what does it mean for a matrix to be invertible, and the process of proving a matrix is invertible, it is time for you to learn the calculation itself of inverting a matrix. We finish this lesson by recommending you to visit the next handout on providing a summarized version of invertible matrix concepts and properties.
Now prepare for our next lesson, see you there!We say that a square matrix (or 2 x 2) is invertible if and only if the determinant is not equal to zero.
In other words, if X is a square matrix and det(X)=0, then X is invertible.
remaining today
remaining today

 . Is it invertible?
. Is it invertible?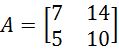 . Is it invertible?
. Is it invertible?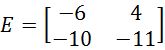 . Is it invertible?
. Is it invertible?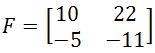 . Is it invertible?
. Is it invertible? . Is it invertible?
. Is it invertible?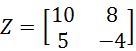 . Is it invertible?
. Is it invertible?

