Congruent vs similar
Before we dig deeper into this chapter of similar polygons, we first have to clarify what is the difference between congruent and similar shapes.
When two shapes are congruent, this means that they are exactly the same in size and shape. You can put the two side by side and see that they are an exact replica of each other.
When it comes to similar shapes, these are shapes that have the same shape but are different in size. You may have worked with similar triangles before, and they're a good example of what similar means. It may be that between the two shapes, one of them is smaller, or one of them is larger. What relates the two shapes is that there's a constant scale factor between them. You'll see this in scale diagrams.
How to find scale factor
Let's say you've got two figures: figure A and figure B. They are both similar, and figure B is an enlargement of figure A. How do you go about finding the scale factor between the two?
The scale factor, as a reminder, is a ratio, so what we're looking for is a ratio that can relate figure A and B. You can calculate the scale factor when you've got an enlargement by putting a side of the bigger figure divided by the smaller figure. That is:
big/small
In this case, it would mean that the scale factor of the enlargement = B side/A side.
Alternatively, if you were looking at the scale factor of a reduction you'd put the smaller figure's side over the bigger figure's side. That is:
small/big
Are the following figures similar?
Here is where we'll teach you how to tell if figures are similar. We learned about both congruent and similar shapes, but we're working with similar polygons in this chapter. After this, you should grasp the basic concept of finding a scale factor and determining whether two shapes are similar.
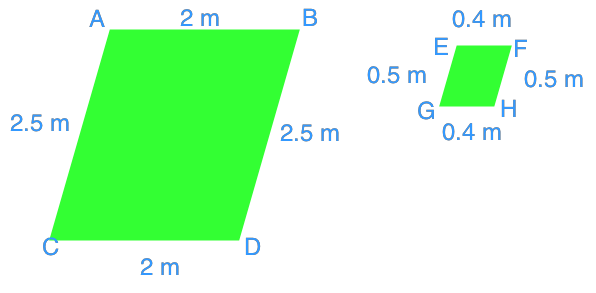
Question 1:
Is each pair of the polygons similar?
Solution:
Use the corresponding sides between the two shapes to calculate the ratio.
We get the same ratios when we take different sides of the polygon. We can therefore conclude that they are similar
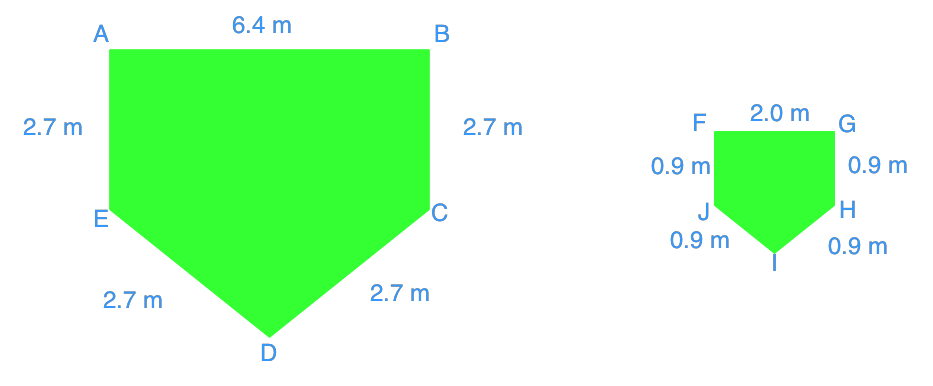
Question 2:
Is each pair of the pentagons similar?
Solution:
Once again, use the corresponding sides to calculate the ratio
We can stop from here and conclude that these are not similar pentagons because they don't have an equal ratio for all sides. Similar shapes must have the same ratio on every one of their sides. If any side breaks the scale factor, you'll know that the shapes aren't similar.
Try playing around with this online diagram that depicts two similar figures. You can scale one of the shapes so that it's enlarged or reduced while still staying similar to the original shape.
To move forward, you'll learn all about congruent triangles and proving their congruence via SSS, SAS, HL, ASA, and AAS.