General form of a line
The general form ax+by+c=0 is one of the many different forms you can write linear functions in. Other ones include the slope intercept form y=mx+b or slope-point form. We can convert the linear function among different forms. These forms of linear function can help us calculate slope, y intercept and a variety of other info.
Standard form of a line
Like the linear functions we've briefly touched on above, another one is the equation of a line in standard form: ax+by=c. In this form, you're able to get the same info as you would if you were given a general form of a line. In this section, we are going focus on these two forms of writing linear functions: the general form equation and standard form.
Practice problems
We'll be trying out some practice problems and walking you through them to help you understand general form and standard form of a line.
Question 1:
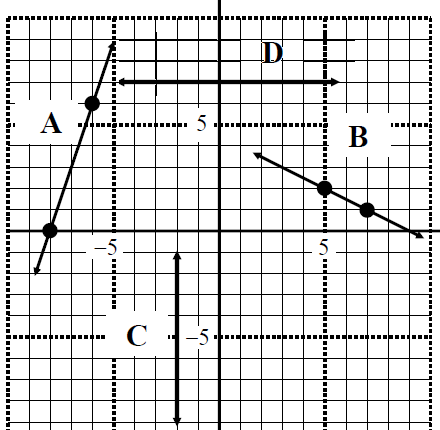
Determine the general form of the following line equations:
Solution:
In this question, we are given a graph with four lines. Let's look at line A only. In order to determine the General form of line A, we can first write the slope intercept form (y=mx+b) of line A. However, we don't have the slope (m) of the line. So, we can use the slope equation to find the slope. We notice that on the graph there are two points highlighted on line A. Let's use the coordinates of these points for the slope equation. So let the higher point (-6, 6) be point 1 and the lower point (-8, 0) be point 2. Now, plug the values into the slope equation, and we get the slope (m) = 3
Now, we put m=3 into y=mx+b, and we'll get y=3x+b. We can then look for b. In order to look for b, we can pick a point on line A and plug the x and y coordinates into y=3x+b. For example, our teacher picked (-8, 0). So, plug in the number and we'll get 0=3(-8)+b, and b=24. The complete linear function in slope intercept form is y=3x+24
Now, we can convert the slope intercept form of y=3x+24 into general from Ax+By+C=0. To convert y=3x+24, we can move everything in the equation to one side of the "=". Finally, we've got our final answer in -3x+y-24=0
We can also covert -3x+y-24=0 into standard form easily. The standard form Ax+By=C and the general form Ax+By+C=0 are similar right? We can get the standard form by just moving the C in the general form from left to the right side of "=". So, -3x+y=24 is the standard form of the linear function line A.
Question 2:
Convert this equation into general form:
Solution:
If we are given the equation of the line, we can rewrite it into general form easily. In this question, we want to rewrite into general form. However, we cannot just move the parts in the equation into Ax+By+C=0 format because we have in the equation. We need to get rid of the denominator first. To do that, we can multiply 5 to equation. We now got 5y=3x+10. In the final step, move 5y to the other side of "=". The answer is 3x-5y+10=0. And the standard form will be 3x-5y+10=0.
You can try using this fun online calculator to help you get the general form of a line from the coordinates of 2 points. Try it out yourself and spot the patterns to writing linear equations in a general form.
Moving along, you'll also eventually learn to calculate parallel and perpendicular line equations. Make sure you grasp the knowledge of the general and standard form first before you proceed!