Ferris wheel trig problems
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Examples
Lessons
- A Ferris wheel has a radius of 18 meters and a center C which is 20m above the ground. It rotates once every 32 seconds in the direction shown in the diagram. A platform allows a passenger to get on the Ferris wheel at a point P which is 20m above the ground. If the ride begins at point P, when the time t = 0 seconds:
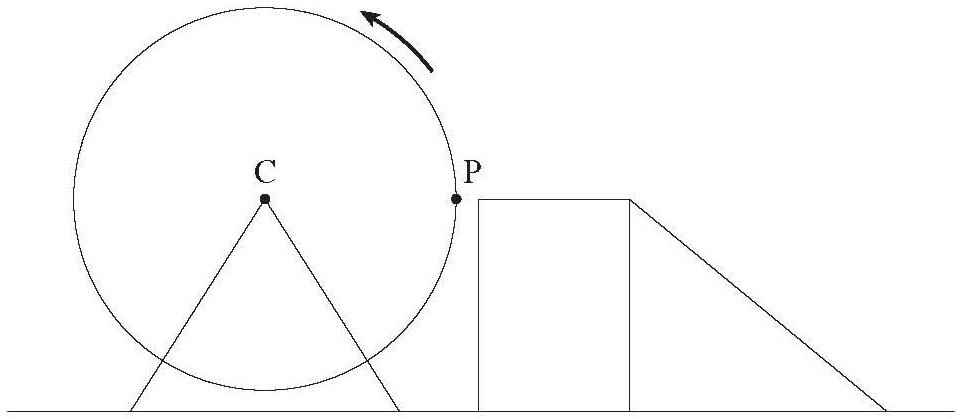
- Graph how the height h of a passenger varies with respect to the elapsed time t during one rotation of the Ferris wheel. Clearly show at least 5 points on the graph.
- Determine a sinusoidal function that gives the passenger's height, h, in meters, above the ground as a function of time t seconds.
- How high above the ground would a passenger be 18 seconds after the Ferris wheel starts moving?
- How many seconds on each rotation is a passenger more than 30m in the air?






