Combinations
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/17
Examples
Lessons
- Compare the difference between the following 2 scenarios:
- How many ways can a president, a vice president, and a treasurer be selected from a class of 20 students?
- How many different committees of 3 people can be selected from a class of 20 students?
- A standard deck of 52 cards consists of:
• 4 suits: diamonds, hearts, spades, and clubs
• each suit has 13 cards
• red cards: diamonds and hearts
• black cards: spades and clubs
• face cards: Jacks, Queens, and Kings
How many different 5-card hands can be formed containing: - Problems with "at least", "at most"
From a standard deck of 52 cards, how many different 5-card hands can be formed containing: - There are 20 members in a student council, 7 boys and 13 girls. How many ways can a committee of 5 people be selected if there must be:
- Five points are marked on a circle. By connecting the points on the circle,
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
How many choices do I have? This lesson can help you with answering this question! Combination is the process of selecting members from a set of items. Combination formula is your best friend in this lesson. Unlike permutations, order doesn't matter in combinations!
Combinations
As you know, we have already talked about the concepts and comparison of permutations vs combinations in our last lesson, still, since these are the two most important processes used in combinatorics, we are dedicating a specific lesson for each of them. Today is the case for combinations!
Let us start with a small review:
How to calculate combinations
We have already learnt that combinations are a way to select objects coming from a complete set, and while permutations are arrangements (ordering) of items, combinations just focus on the specific items selected but does not care about how they are arranged.
To demonstrate how combinations work, we use a set of four boxes:

You are asked to find how many possible combinations can you do with two (any two) boxes out of these four.
Notice that in permutations, the pairs of A B and B A are counted as different even when you have the exact same two letters involved; the same goes for the case of B C and C B, D B and B D, A C and C A, etc. This is the main difference we were referencing before when comparing combinations vs permutations, since in combinations, A B and B A are counted as one combination only! Why? Because a combination is taken as a selection of two distinct items from the set, no matter the order in which they are arranged; thus affirming, that combinations are about how we select items from a set, not how we arrange them.
A formal combination definition would be that when selecting items from a set, each combination is a group (the size of the group depending on what is asked) consisting of distinct items from a set no matter in which order they are arranged. Therefore, when using two out of the four boxes shown in figure 4 we have the following:
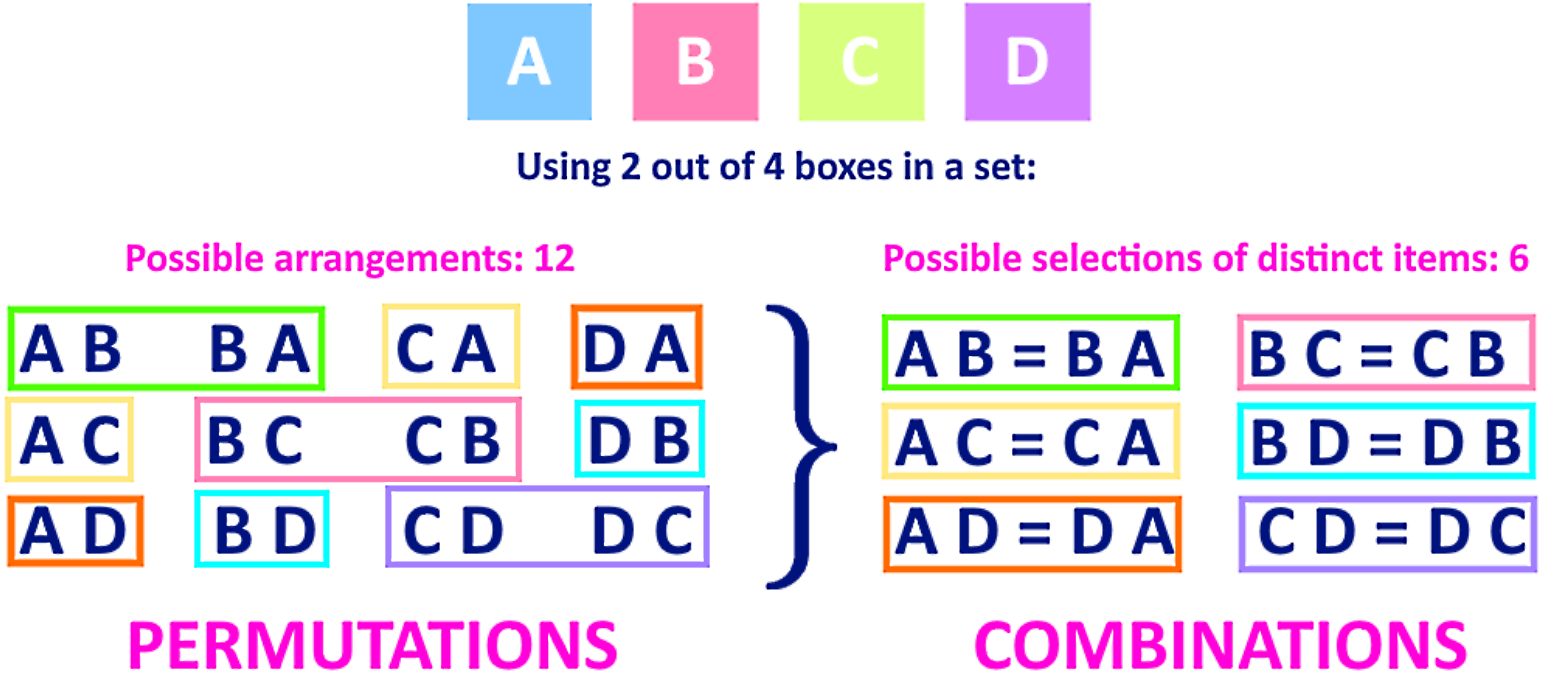
Where you can clearly see the difference between a permutation and a combination, and notice how the number of permutations for the same set and conditions is higher than that of combinations; this is because permutations double count combinations.
With that in mind, the number of combinations formula is defined as:
Where:
nCr = Combinations of r items from a set of n items
n = number of total distinct items in a set
r = items selected from the set
Notice the combinations formula shown in equation 1 is very similar to the permutations formula shown in earlier lessons, the difference comes from an extra factorial in the denominator, which takes care of eliminating the double counting of the permutations.
And so, before we move on to problem examples, let us see a few conclusions: Permutations are about arranging or ordering items obtained from a set, combinations are about selecting distinct items from a set. When looking at the results from combinations and permutations, the main difference between a permutation and combination is that the first pays attention to the order in which the subset of items picked from a total set is arranged, while how many combinations can be done in a subset are characterized by not noticing the way the objects are arranged, just the distinction between the ones selected (no matter how they are placed into positions).
Combinatorics problems
We have named this section as combinatorics problems because we will start with a problem in which permutations and combinations are compared, still, the rest of the problems are focused on our topic for today: combinations.
Example 1
Compare the difference between the following 2 scenarios:1. How many ways can a president, a vice president, and a treasurer be selected from a class of 20 students?
We have seen this problem before in our lesson for permutations, and so, notice that for this problem we are wondering who in particular would end up in each of the three possible committee positions.Therefore, you have that n = 20 and r = 3 to find the possible permutations:
Therefore, there are 6,840 different ways in which the class cabinet can be selected in a class of 20 students, where we have distinction between who ends up in each position from the committee. Now take a look at the next question to see the difference:
2. How many different committees of 3 people can be selected from a class of 20 students?
Now we want to know the different committees of the same 3 people that could be selected, without thinkin who will hold which position, therefore, we use the combination equation (equation 1) to find the fresult, where n = 20 and r = 3, so:
As you can see, this problem has been designed so you can clearly see the difference between permutations and combinations, and even, between the permutations and combinations formula! Once more, the difference relies on the importance of position arrangement for permutations, while the formula for combinations eliminates this by adding a factorial multiple on its denominator.
Example 2
A standard deck of 52 cards consists of:- 4 suits: diamonds, hearts, spades, and clubs
- each suit has 13 cards
- red cards: diamonds and hearts
- black cards: spades and clubs
- face cards: Jacks, Queens, and Kings
1. Any 5 cards (no restrictions)?
Since we have absolutely no restrictions on this case, we can simply calculate the number of combinations of any 5 cards that can result in a hand of cards. For that, we have that n = 52 and r = 5, therefore:
Without any restrictions, we have more than two and a half million combinations!
Before we pass to the next part of this problem, notice that the restrictions we are talking about, do not refer to the order of the cards but they could talk about the colors, suits, numbers or ranks, all of which can be taken into account in case of selecting a hand. For this reason, all of the questions on this example problem are dealt with the combination formula, since the order in which the cards are arranged in a hand has no importance, the distinctions on the cards are made based on their characteristics and once they have been picked in a hand, we dont care in which order they are arranged.
2. All black cards?
Black cards are half of the 52 total cards in a deck (spades and clubs suits) for a total of 26 cards; if we are talking 5-card hands, let us work the total amount of possible combinations of five cards that can be obtained from the 26 which are black ( n = 26 and r = 5):
3. 1 black card and 4 red cards?
For this case we have to pick 1 black card out of the total of 26 possible black cards on the deck; while we also have to pick 4 red cards out of the 26 possible red cards on the deck. Important part to remember is that, it doesnt matter which cards, as long as you have one black and four red. And so, for the choosing of one black card we have that n = 26 and r = 1, therefore:
And for choosing 4 red cards we have that n = 26 and r = 4, therefore:
Therefore, the total amount of combinations for 1 black and 4 red cards in a 5-card hand, is equal to the product of the combinations found above:
4. All face cards?
Since the face cards are the Jack, the Queen and the King (3 cards) in each suit, and we have 4 different suits. It means we have a total of 3 × 4= 12 face cards. Therefore, let us find all possible combinations that we have when all the five cards in a hand are face cards (n = 12 and r = 5):
5. 3 Jacks and 2 Kings?
There are a total of 4 Jacks in all of the card deck, same for the Kings, there are a total of four of them in the deck.
Let us start with the combinations for the Jacks, we need 3 of them out of 4, and so we have that n = 4 and r = 3, therefore:
And for the two Kings we have that n = 4 and r = 2, therefore:
To obtain the total amount of possible combinations of 3 Jacks and 2 Kings in a 5-card hand, we multiply the combinations obtained above and have that:
6. 3 Jacks?
In order to have 3 Jacks in our 5-card hand, this means that the 2 cards left in the hand can be anything that is not a Jack, and there are a total of 48 cards that fit that description. Therefore, we have to combine the combinations for the three Jacks and then the combinations of all of the other cards that can end up in the two positions left in the hand.
The possible combinations for 3 Jacks in a hand of cards were obtained above in equation 10, and so we know there are 4 possible combinations for this to happen.
Now, let us calculate combinations coming from the rest of the 48 possible cards to land in the 2 positions left in our 5-card hand, for which we have that n = 48 and r = 2, therefore:
And so, putting these combined results, we can obtain the total amount of possible combinations of 5-card hands when there are 3 jacks:
Example 3
On this example will take a look at problems using phrases such as "at least" and "at most", such problems can be confusing as to what are the conditions and how to tackle them, so check it out:From a standard deck of 52 cards, how many different 5-card hands can be formed containing:
1. Exactly 2 Diamonds?
If we want exactly two diamonds in our 5-card hand, we know that there are a total of 13 diamond cards on the deck, for 2 positions; then, the remaining 3 positions on a hand, are left for any other card that is not a diamond (there are a total of 39 cards on the deck that are not diamonds). Therefore, to obtain the total number of combinations for 2 diamonds on a card hand, we follow the same process as done in example 2 parts 3, 4 and 5.
Calculating the possible combinations of two diamond cards out of 13:
Now for the possible combinations of any of the 39 cards left, to fill the 3 positions left in the card hand:
And so, the total amount of combinations for exactly 2 diamonds in a 5-card hand is:
The answer to part 1 of example problem 3 is that we have a total of 712,842 possible combinations for 5-card hands with exactly 2 diamond cards.
In the same way we calculated the combinations for exactly 2 diamonds, we can calculate the total amount of combinations for having exactly 0, 1, 3, 4, and up to 5 diamond cards in a 5-card hand:
Notice on equation 18 we mentioned the combinations for two diamond cards in a hand again. Why is this important to know? Because as we have said before, this problem is focused in questions containing phrases at least and at most, and so, we will need these quantities to respond the next two questions.
Keep in mind we already know that all the possible 5-card hands from a 52-card deck are equal to:
We calculated this in the first part of our last problem (equation 4).
Now you have all you need to respond to the next two questions!
2. At least 2 Diamonds?
For the number of combinations possible to have in a 5-card hand that have AT LEAST 2 diamonds, this basically means to check all of the options from equation 18, that take into account 2 diamonds or more. The ones meeting such conditions are:
And so, to find all of the possible combinations of cards in a hand with at least 2 diamonds, we need to add the four quantities shown in equation 20:
Our final answer is: 953,940 combinations with at least 2 diamond cards.
3. At most 2 Diamonds?
For this case, we follow the same process as before, but taking those expressions from equation 18 that have at the most 2 diamonds, and so:
Therefore, we add the results for each of them to find the total we are looking for:
Our final answer is: 2,357,862 combinations with 2 diamond cards at the most.
There are two more examples included on this lessons videos that you should check up, one of them focuses in problems for at least and at most scenarios.
This is the end of our lesson, we recommend you to check out this link on permutations and combinations, which will provide with a simple and summarized explanation of the two in preparation of our last lesson on combinatorics.
We hope you enjoyed this topic, and see you in the next one!
Combination: nCr = number of selections of r items taken from a set of n distinct items (order does NOT matter!!)
= (n−r)!r!n!
= (n−r)!r!n!
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



