Inverse functions
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Intros
0/7
Examples
Lessons
- Graph an inverse
Given the graph of as shown,
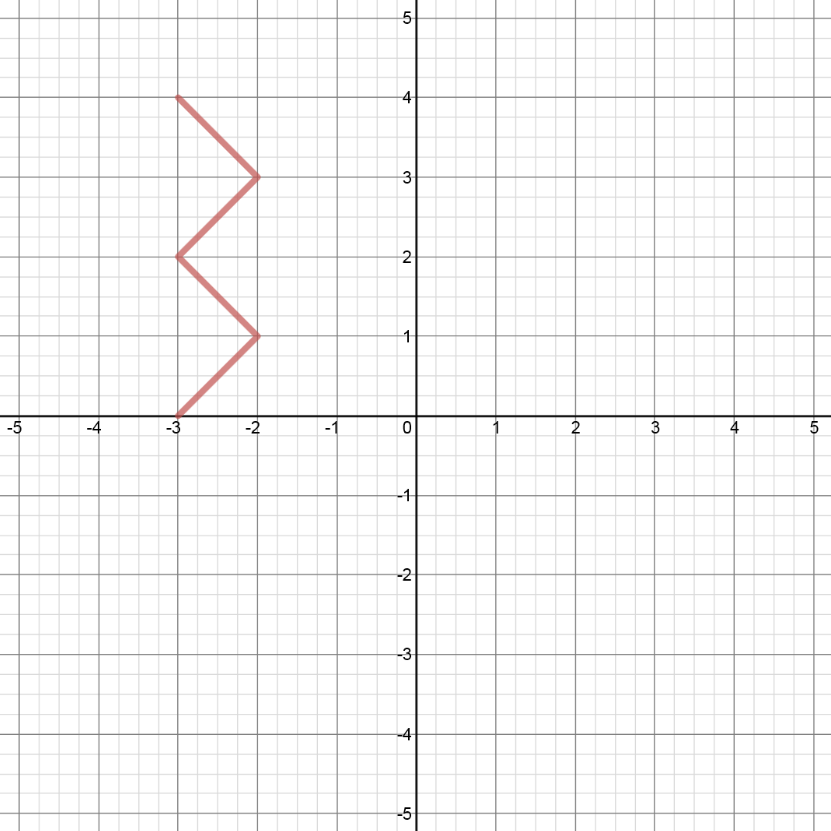
- Sketch the graph of the inverse
in 2 ways:
i) by reflecting in the line
ii) by switching the x and y coordinates for each point on - Is a function?
Is a function?
- Sketch the graph of the inverse
in 2 ways:
- Inverse of a Quadratic Function
Consider the quadratic function: - Determine the equation of the inverse.
Algebraically determine the equation of the inverse , given:






