Derivative of trigonometric functions
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Derivative of trig functions
Before we start learning how to take derivative of trig functions, why don't we go back to the basics? Going back and reviewing the basics is always a good thing. This is because a lot of people tend to forget about the properties of trigonometric functions. In addition, forgetting certain trig properties, identities, and trig rules would make certain questions in Calculus even more difficult to solve. Let's first take a look at the six trigonometric functions.
The 6 Trigonometric Functions
The first trigonometric function we will be looking at is f(x)=sinx. If we are to graph the function, we will get this:
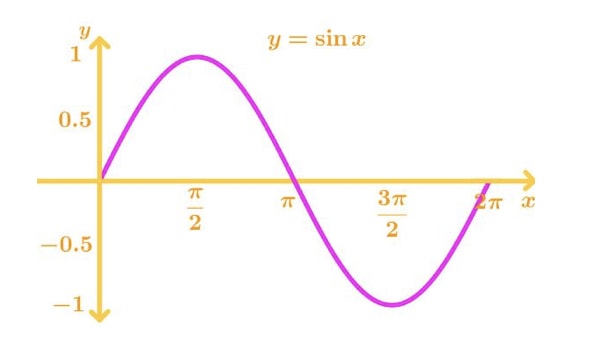
Notice that the function is continuous from [-∞,∞], and it's a nice smooth curve with no sharp turns. This means that sinx is differentiable at every point, and so we will not have to worry about getting something undefined. In addition, we know that the slope at x=2π±πn,n∈I are 0. Hence, the derivative of sinx will always be zero at those points.
Next is the function f(x)=cosx. If we were graph the function, we will get:
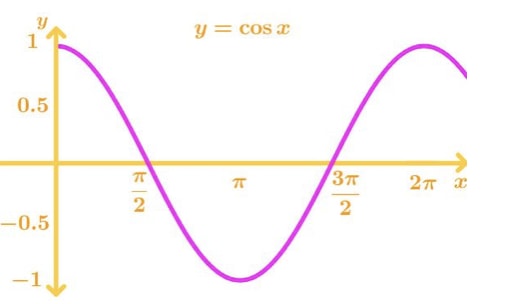
Again note that the function is continuous from [-∞,∞], and it has a nice smooth curve. So cosx is also differentiable at every point. In addition, the slope is equal to 0 at x = 0 ±πn,n∈I. Hence, the derivative will of cosx will be 0 at those points.
Now the function y=tanx is a bit more interesting. It can be rewritten as y=cosxsinx, the graph of this function looks like this:
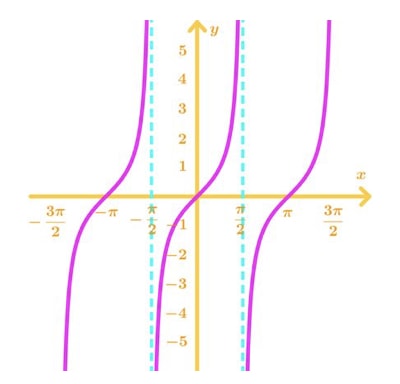
Notice the x values at x=2π±πn,n∈I are undefined, and have vertical asymptotes. This means the derivative of tanx will be not differentiable at those points. One interesting thing to note here is that the slope of tanx is never negative or 0. Hence, we should expect the derivative of tanx to always be positive.
Next are the reciprocal functions of sin cos tan. First, the reciprocal of sinx is cscx. We see the graph of f(x)=cscx looks like this:
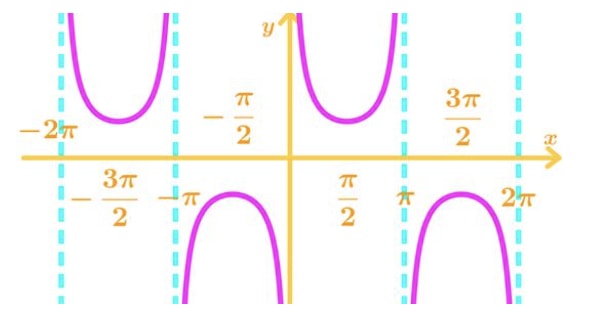
Again, there are vertical asymptotes at x = 0 ±πn,n∈I. So they are not differentiable at those points. In addition, the slope of the function at x=2π±πn,n∈I are 0. So the derivatives are always 0 at those points.
Now the next function is f(x)=secx, which is the reciprocal of cosx. Graphing gives:
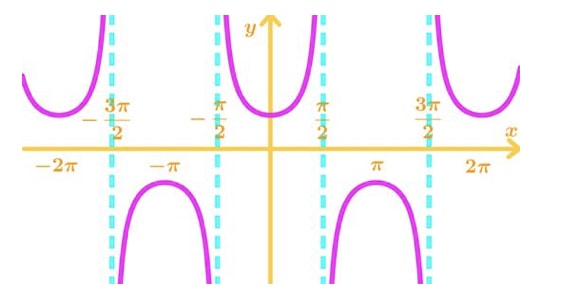
This is very similar to cscx, but the difference is that the role's of the x values has been switched. Now the x values at x=2π±πn,n∈I are the vertical asymptotes and the x value at x=0±πn,n∈I are when the tangent slopes of the function are 0. Hence the derivative of the function is not differentiable at x=2π±πn,n∈I and the derivative is 0 at x=0±πn,n∈I.
The last function is y=cotx.
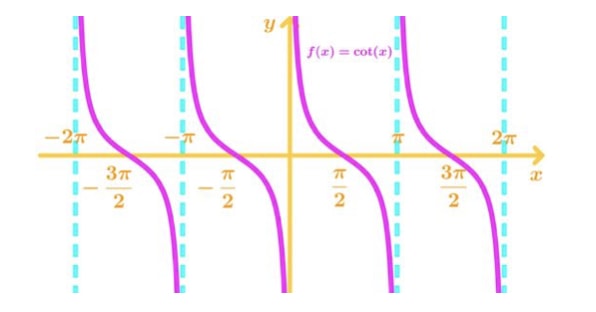
Note that the vertical asymptotes are at x=0±πn,n∈I and the slope of this never positive or 0. Hence, the derivative of this function is always positive, and not differentiable at x=0±πn,n∈I.
Now that we are finished looking at the 6 trig functions, let's now review some of the trigonometric identities that come in handy when taking derivatives.
Trigonometric identities
The first six identities are reciprocal identities, which come in handy when you want your derivatives in a certain form.

Now the most important identities are these three.
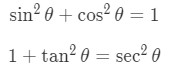
They are very useful when it comes to simplifying derivatives. Now that we've got the basics down, let's go ahead and actually take a look at the derivative of trig functions.
Trig derivatives
The six trig function derivatives are as follows:
1. The derivative of sinx is:
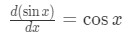
2. The derivative of cosx is:
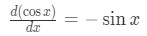
3. The derivative of tanx is:
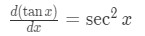
4. The derivative of cscx is:

5. The derivative of secx is:

6. The derivative of cotx is:
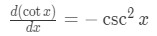
If you really want to know how we get the derivatives, then look at this article below:
Derivative of inverse trig functions
The article shows that the derivative of sin and cosine can be found using the definition of derivative, and the rest can be found with the quotient rule. Make sure you memorize these derivatives well! We will be using these to derive even harder trigonometric functions. You may also want to review the chain rule since a lot of hard trig derivatives require it.
Derivative of sin^2x
We may know that the derivative of sin is cosx, but what about the derivative of sin2x? Let's start with defining the function
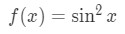
Let's move the square term so that the function becomes:
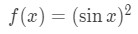
We are going to use the chain rule here. Recall that the chain rule states if you have a function within a function, call it
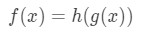
Then the derivative of this function will be
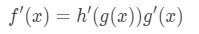
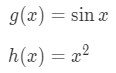
Then, the derivative of these functions will be:
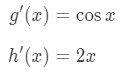
And so the derivative of the function f(x) will be:
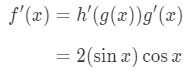
Which is the derivative of sin2x. It wasn't as hard as we thought! Let's look at around hard one.
Derivative of cos^2x
Again, we know the derivative of cosine is −sinx, but what about the derivative of cos2x? We set the function to be
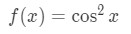
Again, if we rearrange the square in the function, then we will see that
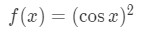
Using the chain rule again, we set:
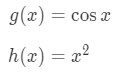
Taking the derivative of these functions gives:
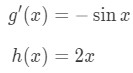
So the derivative of the function will be:
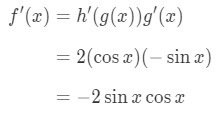
This is very similar to the derivative of sin2x, except we have an extra negative sign! Nevertheless, this is the derivative of cos2x. Let's try to find the derivative of another squared trigonometric function.
Derivative of sec^2x
Again, the key idea of taking the derivative of sec2x is using the chain rule. We define the function to be
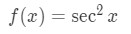
Rearranging the square in the function gives us:
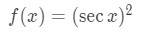
We set:
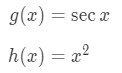
Taking the derivative of secant and x2 gives:
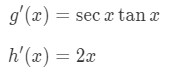
Again in case you forgot, the derivative of sec is secxtanx. Hence, the derivative of sec2x is
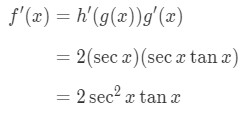
You should know by now that the procedure in taking the derivative of csc2,tan2, and cot2 are the same. So let's take a look at other trigonometric derivatives.
Derivative of sinx^2
Now before you get confused, this is a function that looks similar to sin2x. However, sin2x is different from sinx2. So of course, there derivatives will also be different. We define the function to be:
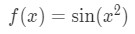
Note that we will use the chain rule here. We set
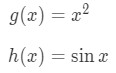
We know the derivative of g(x) is 2x and the derivative of sinx is cosx. So
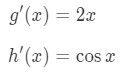
Hence the derivative of the function will be:
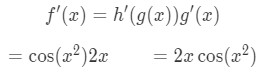
Now let's try the same thing for finding the derivative of cosx2!
Derivative of cosx^2
We define the function to be:
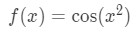
Using the chain rule we set:
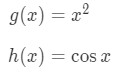
Taking the derivative of g(x) gives 2x and taking the derivative of cosine gives −sinx. So
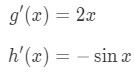
Hence the derivative of the function is:
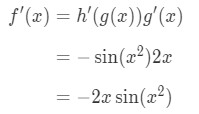
Let's do two more before we start doing even harder trigonometric functions.
Derivative of tanx^2
Again, the function we have is:
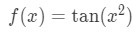
Using the chain rule, we set g(x) and h(x) to be:
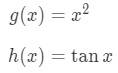
The derivative of x2 is 2x, and the derivative of tan is sec2, so
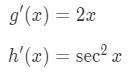
Using the chain rule formula, we get the derivative of tanx^2 is:
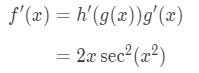
This one is a bit harder because the derivative seems to have two squares; one from secant and one from x. Lastly, let's look at the derivative of cscx2.
Derivative of cscx^2
The function we have is:
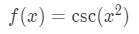
In order to do chain rule, we let two functions, g(x) and h(x), to be:
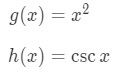
The derivative of x2 is 2x, and the derivative of csc is -cscxcotx, so
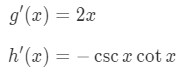
Using the chain rule formula, we get that the derivative of cscx2 is:
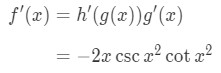
http://tutorial.math.lamar.edu/Classes/CalcI/DiffTrigFcns.aspx
Now it's time move on and take a look at some questions which have applications to the slope of a function.
Slope of a trigonometric function
Suppose we want to find the slope of the function:
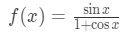
At the point x=0. How would we do it? Well, realize take find the slope of a function is just the same as taking the derivative. This will require using the quotient rule since the function is a quotient.
Recall that the quotient rule says the following:
If you have a function
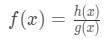
Then the derivative of this function will be:
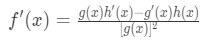
So if we were to set
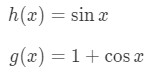
Then their derivatives will be:
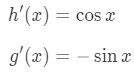
Hence, using the quotient rule gives the derivative:
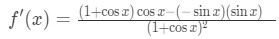
Simplifying this equation gives:
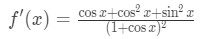
To simplify this equation, we would want to use the trigonometric identity:
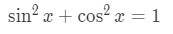
So our equation becomes:
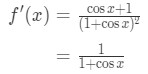
Now that we have the derivative, all we have to do is plug in the point x=0 to get the slope. Hence,
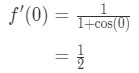
Thus, the slope of the function at the point x = 0 is exactly 21. However, what if we were given the tangent slope of a function at a specific point, and we need to find that point?
Finding the points given the slope
Suppose you are given that the function is:
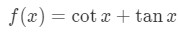
And you want to find the set of points which the slope of the tangent line is equal to 0. This means we need to take the derivative and set it equal to 0 to find the x values. Note that the derivative of tan is sec2 and the derivative of cot is –csc2, so
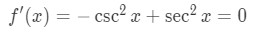
Note that the reciprocal identities state that:
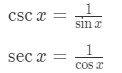
Hence, our equation becomes:
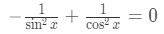
Let's try to solve for x in this equation. See that:
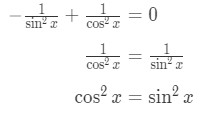
Moving the sin2x to the other side gives:
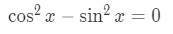
Recall the trigonometric identity
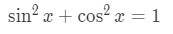
We can actually isolate sin2 by itself in the equation so that:
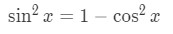
Substituting this into our equation gives:
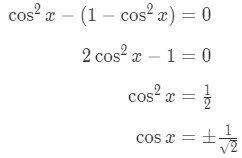
Now we need to look at the positive case and then the negative case. For the positive case we have:
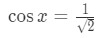
See that since x is not bounded, then were are infinitely many solutions. In fact, we know the solutions are:
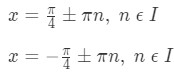
Now if we were to look at the negative case, then we have:
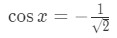
Again, there are infinitely many solutions for this. The solutions for this equation will be:
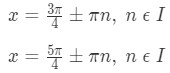
Now let's take a look at the four solutions as a whole. Notice that the two pairs are the same
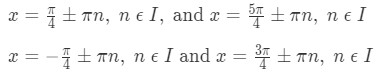
So we can just exclude the two solutions and say that the solutions are
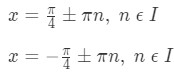
So we can conclude that these are the set of points in which the slope of the function is equal to 0.
Derivative of Inverse Trigonometric Functions
Now the Derivative of inverse trig functions are a little bit uglier to memorize. Note that we tend to use the prefix "arc" instead of the power of -1 so that they do not get confused with reciprocal trig functions. Regardless, they mean the same thing. For example, derivative of arctan is the same as the derivative of tan−1.
Here are the inverse trig derivatives that you will need to know.

Note that the arctan derivative is similar to the derivative of arccot, except there is an extra negative sign. Coincidently, we see that the derivative of arcsin is similar to the derivative of arccos. The difference again is the negative sign. We will not be doing any examples of Derivative of inverse trig functions here. However if you are interested, then please look at this article here:
Derivative of inverse trig functions
The article here gives a detailed step-by-step solution in deriving these derivatives.
dxdsinx=cosx
dxdcosx=−sinx
dxdtanx=sec2x
dxdcotx=−csc2x
dxdsecx=secxtanx
dxdcscx=−cscxcotx
remaining today
remaining today



