Double-angle identities
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Using double angle identities in trigonometry
Identities in math shows us equations that are always true. There are many trigonometric identities (Download the Trigonometry identities chart here ), but today we will be focusing on double angle identities, which are named due to the fact that they involve trig functions of double angles such as sinθ, cos2θ, and tan2θ. It's hard to simplify complex trigonometric functions without these formulas.
How to use double angle identities Firstly, what are double angle identities? Let's take a look at the trigonometry identity chart here:
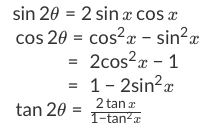
For now, let's take a look at some double angle identities examples. Using the above trig identities cheat sheet, we can go through this trigonometric identities tutorial:
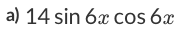
If you look at the trigonometry identity chart, you won't find a number, followed by sine, then cosine—not in quotient identities, not in reciprocal identities, not in Pythagorean identities, and not in sum and difference identities.
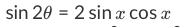
For both formulas we have a sine, cosine, which is nice. But the number in front is of our problems is 14, whereas in the double angle identity, the number in front is 2. What should be our next step? Multiply the whole expression by 7. That will give us 7(sin2θ). Multiplying this into the right side of the equation, we will get:

Let ? = 6x, which gives us:

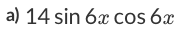

Formulas:sin2θ=2sinxcosx
cos2θ=cos2x−sin2x
=2cos2x−1
=1−2sin2x
tan2θ=1−tan2x2tanx
Basic Concepts
Related Concepts
remaining today
remaining today



