Polynomial long division
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
Examples
Lessons
- Use long division to divide polynomials
Apply long division, and then use the result to write the division statement in 2 ways. - Watch out for "Missing Terms"! → Use "Placeholder"
Operate long division. - Application of a Division Statement
Given the long division as shown:
Determine the polynomial P(x). - Determine "Factors"
(6x2+7x−5)÷(3x+5)- Operate long division.
- Write the division statement.
- Is (3x+5) a factor of (6x2+7x−5)? Explain.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Dividing Polynomials
Sometimes, most often when dealing with rational expressions, it will be necessary to divide polynomials. This process can seem daunting, especially when we have larger and larger degrees in more complex polynomials. Luckily, however, there are two tried-and-true methods to help with this task! These two methods are synthetic division and long division.
Steps in Solving Synthetic Division:
Synthetic division is a "quick" process that allows one to more efficiently divide polynomials, compared to using good ol' fashioned long division. Despite being more efficient, the synthetic division steps involve equal work, and you need to carefully keep track of all values.
In division, we use the coefficients of the divisor and the dividend, rather than the entire polynomials themselves. We define divisor as the polynomial which we are dividing by, and we define dividend to be the polynomial that we are dividing by the divisor.
Upon completion of this process, we are left with the quotient and a remainder. We define quotient as the "solution" to the division, and we define remainder to be whatever could not be further divided to give a "whole" solution, which will become more clear in the example later.
In summary, division, both by synthetic and long division, can be written in two ways:
1) dividend = (divisor) (quotient) + remainder
2) divisordividend=quotient+divisorremainder
Now that we have a firm grasp of the techniques and terminology behind division of polynomials, let's take a look at some synthetic division problems.
Example:
Divide the following polynomial by (x-4):
- Step 1: Setup the Synthetic Division
Before we can start dividing, it is important to note that we must write out terms for all terms of the quartic function, even if the coefficients are zero.
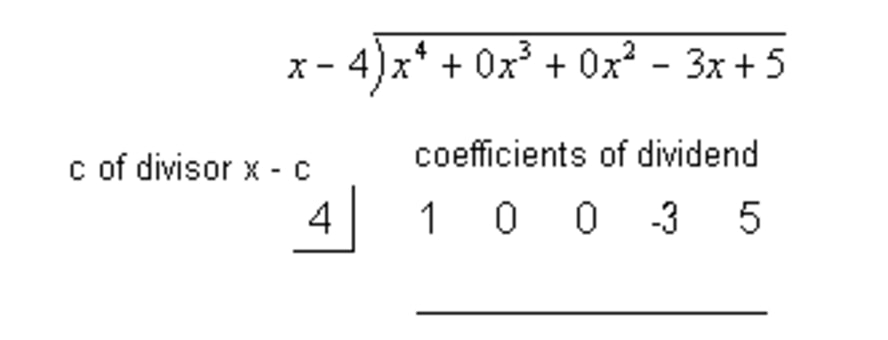
Setup the Synthetic Division - Step 2: Bring Down the Leading Coefficient to the Bottom Row
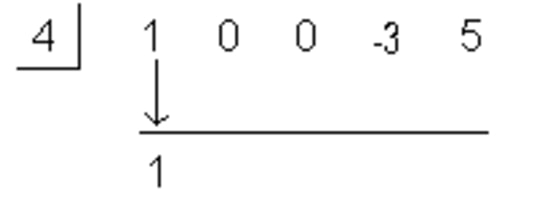
Bring Down the Leading Coefficient to the Bottom Row - Step 3: Multiply c by the Value Just Written on the Bottom Row
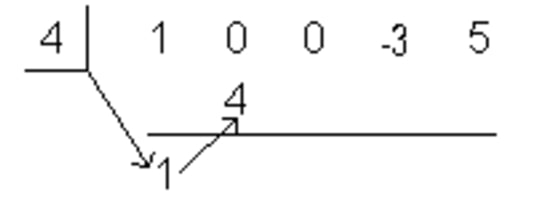
Multiply c by the Value Just Written on the Bottom Row - Step 4: Add the Column Created in Stem 3
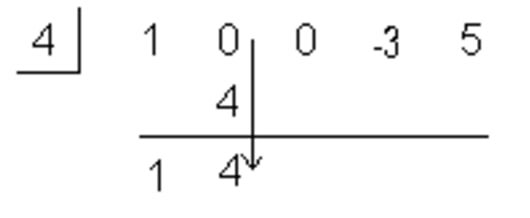
Add the Column Created in Stem 3 - Step 5: Repeat until Done
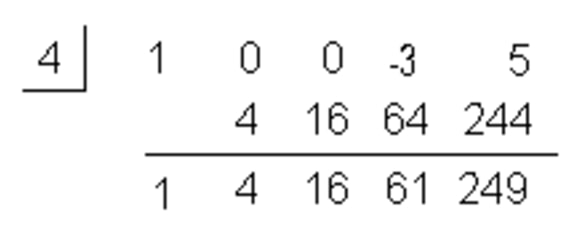
Repeat until Done - Step 6: Write out the Final Answer
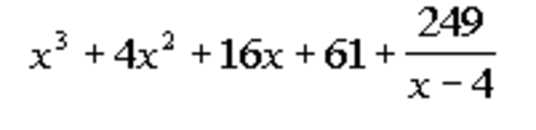
Write out the Final Answer - In this case, the division remainder is 249. We can express this by simply writing it divided by our original divisor, (x-4).
Steps in Solving Polynomial Long Division:
As discussed in the previous section on synthetic division, the terminology and theory behind long division is identical. What is different is the long division steps. This is most clear in some example problems.
Example 1:
Divide using long division: 8x3−14x2+7x−1÷2x−5
- STEP 1: Find first term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial. Pull down the remaining polynomials.

Find first term by dividing the first term of the numerator by the first term of the denominator, - STEP 2: Find second term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial then pull down the remaining polynomials.
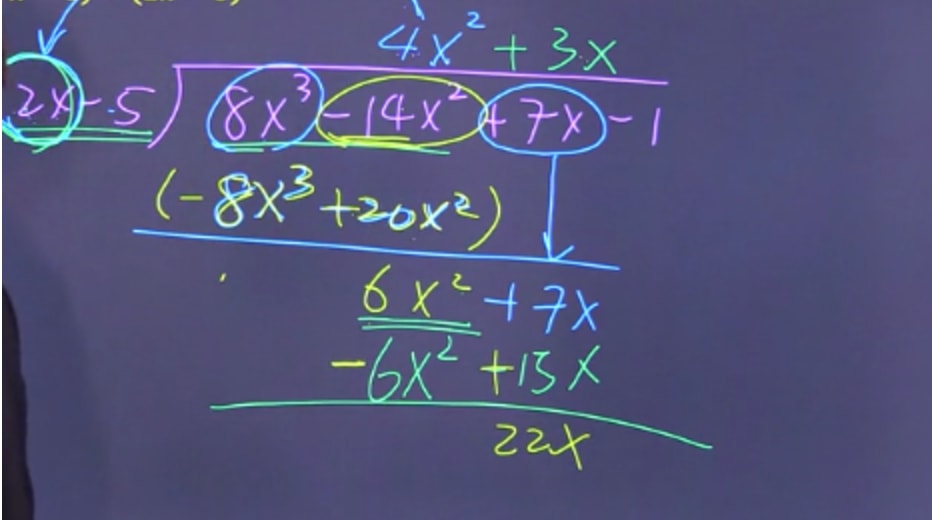
Find second term by dividing the first term of the numerator by the first term of the denominator - STEP 3: Find last term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial.

Find last term by dividing the first term of the numerator by the first term of the denominator - In summary, we are left with the following since the remainder is a smaller degree polynomial than the divisor:
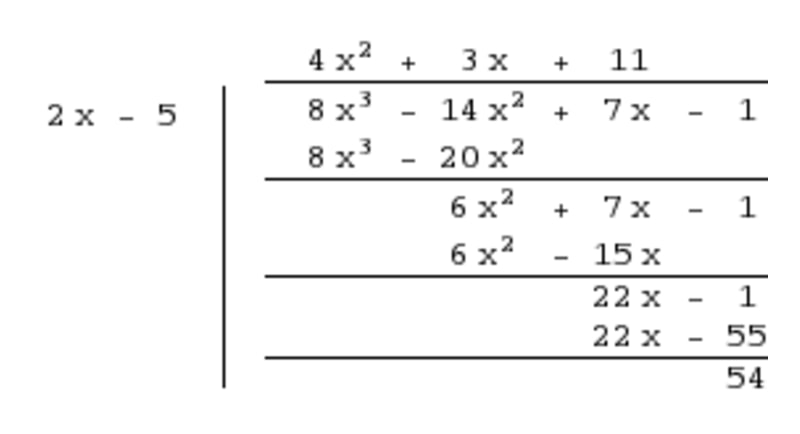
remainder is a smaller degree polynomial than the divisor 1
Example 2:
Divide using long division: (x−2)(x3+5x−11)
- STEP 1: Find first term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial. Pull down the remaining polynomials.

Find first term by dividing the first term of the numerator by the first term of the denominator - STEP 2: Find second term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial then pull down the remaining polynomials.
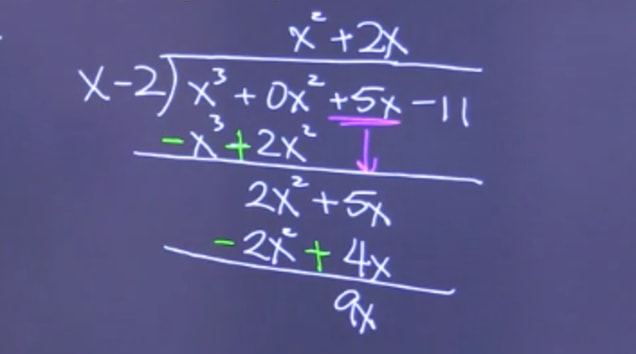
Find second term by dividing the first term of the numerator by the first term of the denominator - STEP 3: Find last term by dividing the first term of the numerator by the first term of the denominator, and put that in the answer. Then multiply the denominator by that answer, put that below the numerator and subtract to create a new polynomial.

Find last term by dividing the first term of the numerator by the first term of the denominator - In summary, we are left with the following since the remainder is a smaller degree polynomial than the divisor:
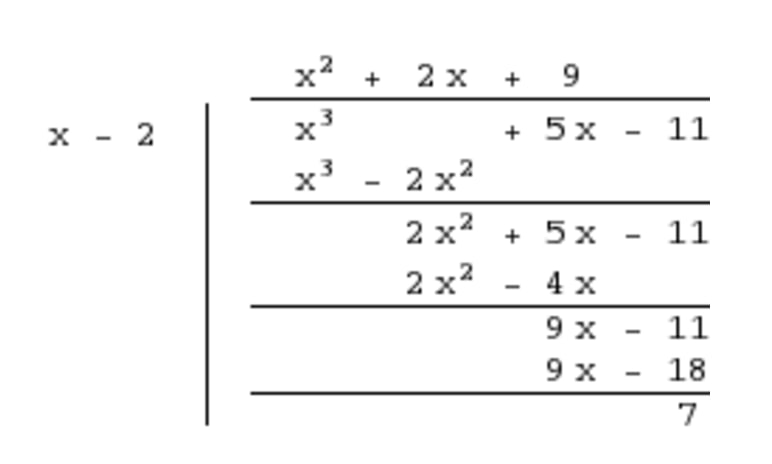
remainder is a smaller degree polynomial than the divisor 2
Remainder Theorem:
As a final topic of discussion, to save time, the remainder theorem is a powerful for dividing polynomials when things are too complicated or time is short.
According to the Remainder Theorem:
If we divide a polynomial f(x) by (x-c), the remainder of that division is simply equal to f(c).
This theorem is especially helpful because it reduces the amount of work we have to do to solve these types of problems. Without this theorem, we would have to go to the trouble of using long division and/or synthetic division to solve for the remainder, which is difficult and time consuming.
And that's everything! You now have all the tools needed to divide any pair of polynomials. Try practicing and mastering synthetic and long division before using the handy trick of the remainder theorem, first. For a useful division calculator, check out this great link here. Lastly, for further and related study, see our videos on rational expressions, dividing rational expressions, dividing polynomials, and the integration of rational functions by partial fractions.
i) dividend = (divisor) (quotient) + remainder
ii) divisordividend = quotient + divisorremainder
Basic Concepts
Related Concepts
remaining today
remaining today




