Solving polynomial equations
All You Need in One PlaceEverything you need for better marks in primary, GCSE, and A-level classes. | Learn with ConfidenceWe’ve mastered the UK’s national curriculum so you can study with confidence. | Instant and Unlimited Help24/7 access to the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
What is the zero product property
The zero product property definition tells us that if:then either a or b has to equal 0.
Logically, this makes sense. Any number multiplied by 0 gives us 0. No other combinations can give us this. Therefore, one of the two unknown numbers must be 0.
How to solve polynomials
When we're asked to solve a polynomial, we're actually being asked to find the roots where the function equals 0. You can see how the above zero product property can come in handy! So how do we start solving polynomials? We'll have to do some isolating.
How to isolate a variable
In order to figure out when a polynomial equals 0, we'll have to isolate the variable that is in the equation so that we can find its value. This is like how we solve two-step linear equations. Let's try it out with a simple polynomial equation. Do you know how to solve for x?
Since we don't know what x is, we'll have to isolate it onto one side to see what it equals. In this case, let's start with moving the 1, and then the 2 that's next to the x.
When you've got a positive on one side and you've got to move it to the other side of the equal sign, simply reverse the sign to negative. If it's negative and you've got to move it, it'll become positive. Similarly, if you have to multiply on one side and now you're trying to move it to the other side, you'll have to divide it. If you've got a division, it'll become multiplication on the other side of the equal sign.
If you've got a variable on both sides of the equal sign, you'll still have to group it to one side in order to find its value.
Example problems
Question 1:
1a) Solve the equation:
4x2−9=0
Solution:
Since we're dealing with a degree of a polynomial (in this case it's the power of 2), when you move a square to the other side of the equal sign, you'll have a square root. A note is that all positive real numbers has two square roots—one that's positive and one that's negative. Therefore, we'll put a ±sign in front of the square root to indicate we'd like both the negative and positive in our final answer.
4x2=9
x2=49
x=±49
x=±23
1b) Solve the equation:
(2x−3)2=1
Solution:
2x−3=±1
2x−3=±1
2x=±1+3
x=23±1
x=2,1
Question 2
Solving the equation:
3x2−13x−10=0
We have to factor the polynomial before solving for x so that we can get it into a form that looks like we're about to do distributive property on it.
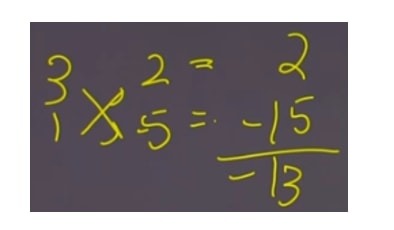
After factoring, we have:
(3x+2)(x−5)=0
To solve for x, we can separate (3x+2)(x−5)=0 into two equations using the zero product property:
(3x+2)=0,and (x−5)=0
Isolate and solve for x
3x+2=0
3x=−2
x=3−2
x−5=0
x=5
So, in this question, x=3−2 and x=5
Not sure about your answers? Here's an online polynomial equation calculator you can use to check your answer when solving polynomial equations.
Want to move on? You can take a look at these related lessons to improve on your understanding:
- Determining the number of solutions to a linear equations
- Solving systems of linear equations by graphing
Basic Concepts
remaining today
remaining today



