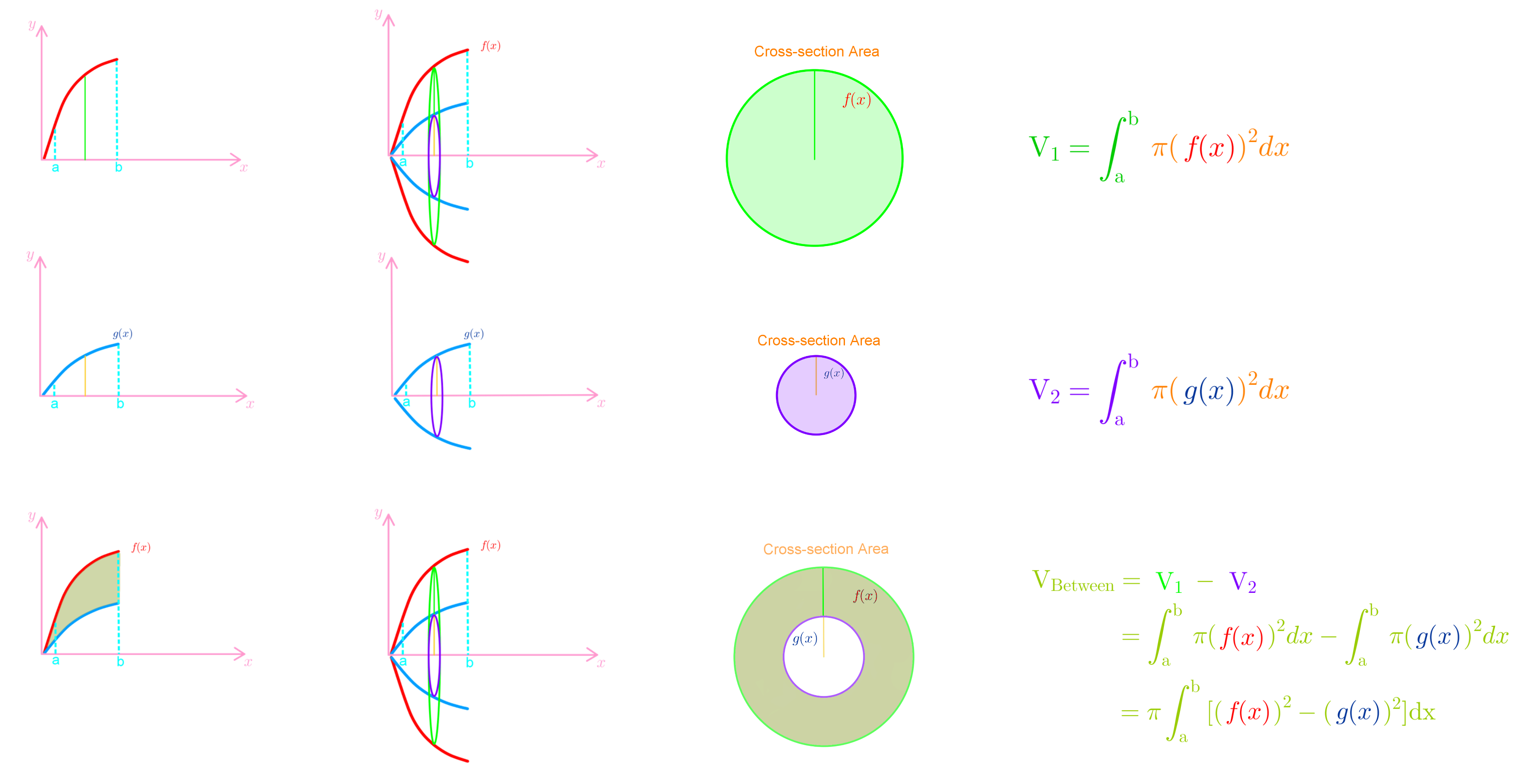
Volumes of solids of revolution - Disc method
All You Need in One PlaceEverything you need for better marks in primary, GCSE, and A-level classes. | Learn with ConfidenceWe’ve mastered the UK’s national curriculum so you can study with confidence. | Instant and Unlimited Help24/7 access to the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
0/1
Intros
0/6
Examples
Lessons
- The region bounded by the graphs of , ,, and is revolved about the
x-axis. Find the volume of the resulting solid.
- Find the volume of the solid obtained by rotating the region bounded by ,
, and about the y-axis.
- Find the volume of the solid obtained by rotating the region bounded by , and
about the x-axis.
- Find the volume of the solid obtained by rotating the positive region bounded by ,
- Find the volume of the solid obtained by rotating the region bounded by , and about .