Solving expressions using 45-45-90 special right triangles
All You Need in One PlaceEverything you need for better marks in primary, GCSE, and A-level classes. | Learn with ConfidenceWe’ve mastered the UK’s national curriculum so you can study with confidence. | Instant and Unlimited Help24/7 access to the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Table of Contents:
- Special right triangles 45 45 90
- How to solve 45 45 90 triangle
- What is the 45 45 90 triangle theorem?
- Does the pythagorean theorem work for 45 45 90 triangles?
- How to prove the 45-45-90 triangle theorem?
- What are the lengths of the sides of a 45 45 90 triangle?
- What is the hypotenuse of a 45 45 90 triangle?
- What are the ratios of a 45 45 90 triangle
- How to calculate area of 45-45-90 right triangle
- Does a rhombus make 45-45-90 triangles?
- Walk through Example and Practice with 45 45 90 triangles
Special right triangles 45 45 90
Special triangles are a way to get exact values for trigonometric equations. Most trig questions you've done up till now have required that you round answers in the end. When numbers are rounded, it means that your answer isn't exact, and that's something that mathematicians do not like. Special triangles take those long numbers that require rounding and come up with exact ratio answers for them.
There's not a lot of angles that give clean and neat trigonometric values. But for the ones that do, you will have to memorize their angles' values in tests and exams. These are the ones you'll most typically use in math problems as well. For a list of all the different special triangles you will encounter in math.
One of these triangles is the 45 45 90 triangle. It is an isosceles triangle, with two equal sides. Since you'll also find that this triangle is a right-angled triangle, we know that the third side that is not equal with the others is the hypotenuse. You also happen to know a nice formula to figure out what the length of the hypotenuse is (the Pythagorean Theorem) and we'll show you how it will be used. If you wanted to take a look at more examples of the 45 45 90 triangle, take a look at this interactive online reference for this special right triangle.
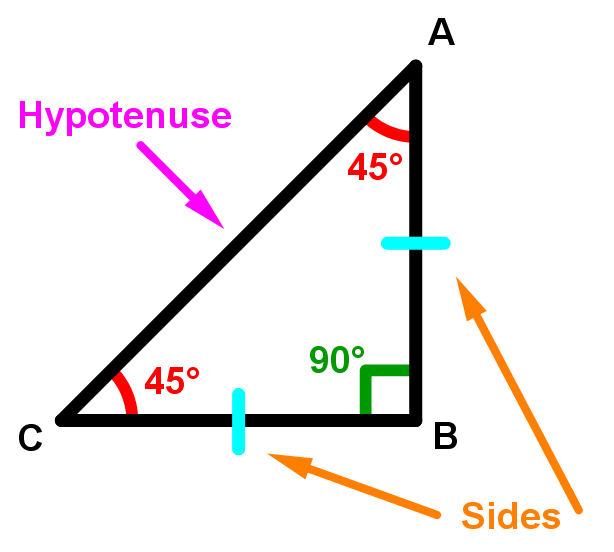
How to solve 45 45 90 triangle
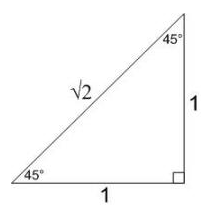
To help demonstrate what the special right triangle with 45 45 90 as its angles looks like, as well as explain the values that you'll have to work with going forward, we'll use the below example. It shows a standard 45 45 90 triangle that can help you understand the ratios that come about when this triangle is used.
1 is chosen to be used as the length of the sides that are equal in this special triangle, since that's the simplest to work with. So how do we find the hypotenuse?
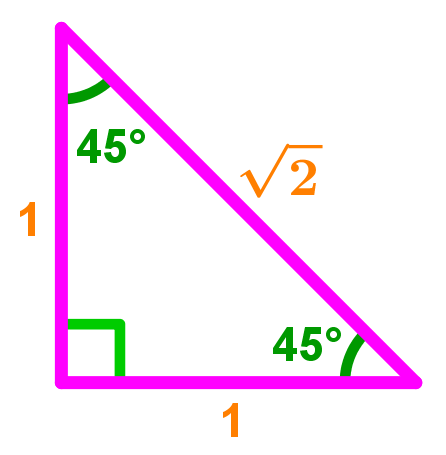
This is an isosceles right triangle. Since it is a right triangle, we can use Pythagorean Theorem to find the hypotenuse.
c2=12+12
c2=1+1=2
c=2
With the hypotenuse, we have information to determine the following:
cos45° =21
tan45° =11=1
You can see that we are looking at the "theta" of 45 degrees, and you should remember SOHCAHTOA, which helps you remember which sides you'll need to take to find the sine, cosine, and tangent. That is how we've got that the sine is 21, since 1 is the length of the side that is opposite of 45 degrees, and the hypotenuse is 2. For cosine, you'll need the adjacent over the hypotenuse, which gives you 21. Lastly, for the tangent, it's opposite over adjacent, giving you 11, or in a more simplified form, just 1.
Knowing that you'll need to memorize these values, you can opt to commit them to memory, or you can redraw this triangle and use SOHCAHTOA to help you find the angle's ratios. Either way, we hope that by explaining the components of the triangle to you, you now have a better understanding of the 45 45 90 special triangle and how its ratios came about.
What is the 45 45 90 triangle theorem?
The 45 45 90 triangle theorem states that 45 45 90 special right triangles that have sides of which the lengths are in a special ratio of 1:1:2 and two 45° angles and one right angle of 90°.
Let us take a closer look at the relationship of these ratios and ask why 45 45 90 special right triangle all share these following properties:
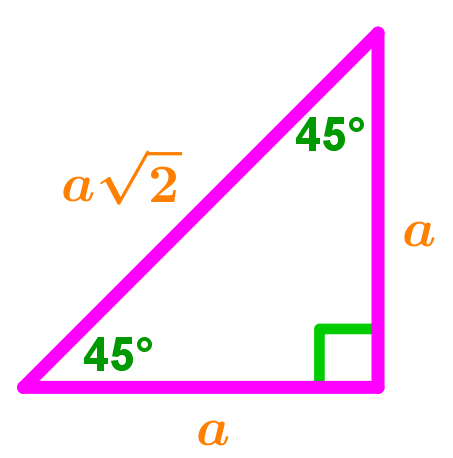
1. As an isosceles triangles, the length of 2 sides of any special 45 45 90 triangle will always be the same. This is depicted by the letter a in the diagram above. As a consequence of having equal lengths, a corresponding property of these two sides is that they have angles of the same size. This can be identified by the two 45° angles in the diagram above. Since the total sum of angles in a triangle always equal to 180°, the remaining angle, is 90°, always known as a right angle. This is where the name of this special triangle is derived.
2. The hypotenuse of any special 45 45 90 triangle will have a length of a2. This is a special relationship found in 45 45 90 triangles. This value is derived by taking the length of any of the two equal sides (i.e. a) and multiplying it by the radical 2. This radical is the simplest form of the length of a hypotenuse in a 45 45 90 triangle. It can be calculated by using the pythagorean theorem as seen earlier above when we learned how to solve 45 45 90 degrees triangles.
Does the pythagorean theorem work for 45 45 90 triangles?
As discussed by our expert tutors here at StudyPug, the pythagorean theorem describes the relationship of the lengths of each side in right angle triangles. This is just one of the many triangle equations you may recall from in Geometry. Since the 45 45 90 triangle is indeed an example of a right angle triangle, we are able to utilize the pythagorean theorem to identify the length of any of the sides. What makes the sides of a 45 45 90 special right triangle particularly easier to solve is that two of the sides are of equal length.
So yes, using the pythagorean theorem and being given just one of the lengths of any side, we are able to use the pythagorean equation, a2+b2=c2 , where c is the hypotenuse and a and b represent the two equal sides of a 45 45 90 triangle.
How to prove the 45-45-90 triangle theorem?
There are two ways we can validate the 45-45-90 triangle theorem. Remember that with 45-45-90 triangles, we are provided with the angles and the ratios of the length of the sides. This immediately tells us that what we will have to solve are simply dimensions of 45-45-90 triangle to support the 45-45-90 triangle theorem. Knowing these pieces of information, we are able to double check our work by working backwards to show that the length of the sides are in accordance to the ratios. Remember that being an isosceles triangle, half the work is done in simply finding either the length of the adjacent or opposite sides of the 45-45-90 triangle. These values will be equivalent!
The two ways to validate the 45-45-90 triangle theorem is through:
1. Using the pythagorean theorem2. Using the special ratio of 1:1:2
What are the lengths of the sides of a 45 45 90 triangle?
Using the pythagorean theorem – As a right angle triangle, the length of the sides of a 45 45 90 triangle can easily be solved using the pythagorean theorem. Recall the pythagorean theorem formula: a2+b2=c2. In any given problem you will either be given the value of a, b, or c. Since a and b, the opposite and adjacent sides of any 45 45 90 triangle are equivalent, knowing the length of side a, gives you the length of side b, or vice versa. Knowing this, we can simply plug these values into the pythagorean theorem formula to find the value of c, the length of the hypotenuse.
Now what if we are just given the length of the hypotenuse (i.e. c)? We can simplfiy the pythagorean formula to solve for the length of the both a, and b, the opposite and adjacent sides of the 45-45-90 triangle. The length of both a, and b are equal since we are dealing with an isoceles triangle.
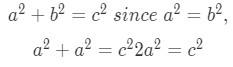
With the simplfied equation, we can simply plug in the value of c, we were given initially, and solve for both a and b, the two other sides of the 45-45-90 triangle. Knowing the 45 45 90 triangle sides lengths, we can now show that they are in the special ratio of 1:1:2.
Method 2: Using the special ratio of 1:1:2 - Now this method is a lot faster and produces exact values. If the question asks for you to leave your answers in simplified radical form or to anwer with exact values, use this method! Keep in mind that because of this special relationship, this ratio can also be generalized and written as x:x:x2 (see image below).

Now say we were given the value of one side to be 8.
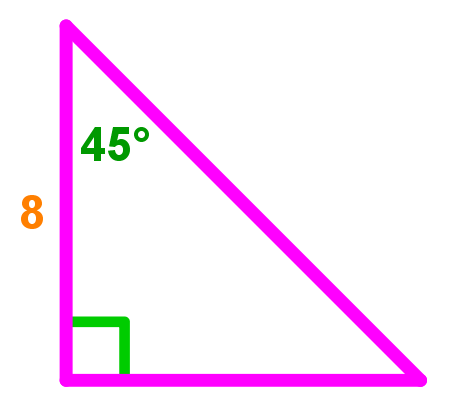
Taking this value and plugging into our standard ratio formula, x:x:x2, we see that we have quickly and easily solved for all sides of our 45 45 90 triangle – 8:8:82.
Now how do simplify these ratios to show that the dimensions of this right angle triangle is in accordance with the ratios of a 45 45 90 triangle? Since the greatest common factor between these ratios is 8, we can divide and simplify this ratio by 8.
=1:1:12
=1:1:2
We have now shown that this right angle triangle, satisfies the requirements of the 45 45 90 right angle triangle theorem.
What if we were given the value of the hypotenuse (i.e.x2) to be 2?
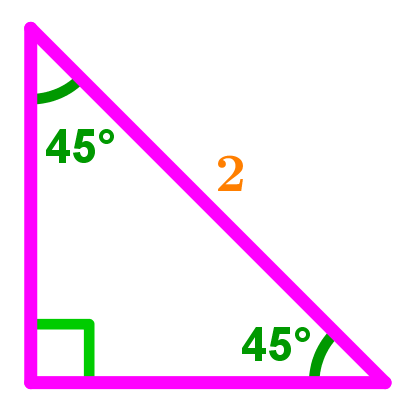
For these types of questions there is the extra step of solving for x:
x=22=22⋅22=222=2
So plugging these values into our generalized ratio formula we have 2:2:2. To simplify, we can divide by 2.
=1:1:22
To simplify 22 we multiply both the denominator and numerator by 2
This involves rationalizing the denominator:
Therefore we see that once again we yield a ratio of 1:1:2, meeting the standard ratios of the special 45 45 90 right angle triangle!
Use any of these methods or 45-45-90 triangle formulas to help you solve any 45-45-90 triangle problem!
What is the hypotenuse of a 45 45 90 triangle?
The hypotenuse of a 45 45 90 triangle could really be any number – the only thing that would matter is that the value of the hypotenuse relative to the other sides of the triangle, follows the special ratio we previously discussed: 1:1:2.
Since the value of a hypotenuse could be any rational, irrational, or real number, a 45 45 90 triangle could have the smallest hypotenuse of any triangle! However, the infinitesimal nature of these kinds of numbers makes a myriad of possibilities for the length of the hypotenuse of a 45 45 90 triangle. This makes it impossible to say that 45 45 90 triangles have the smallest hypotenuses. Check out this interactive 45 45 90 triangle to see this in action!
So how to find hypotenuse lengths of 45 45 90 triangles? Scroll up to see how we calculate hypotenuses of 45 45 90 triangles!
What are the ratios of a 45 45 90 triangle
In its simplest form, the ratios of the length of sides in a 45 45 90 special right angle triangles should be 1:1:2. Recall that the 45 45 90 special right angle triangle is an isosceles triangles with two equal sides and the one larger side (i.e. hypotenuse definition).
How to calculate area of 45-45-90 right triangle
Like many other fundamental triangle formulas, the formula to calculate the area of a triangle should be one you may remember: A=21⋅b⋅h. With special right triangles with angles of 45 45 90, this same formula can be applied.
Let's examine this in our most basic 45-45-90 right triangle:

=21⋅1⋅1
A=0.5
An alternative way to solve for the area of a 45-45-90 right triangle involves the use of a special 45 45 90 triangle formula derived from the formula used to calculate the area of a square.
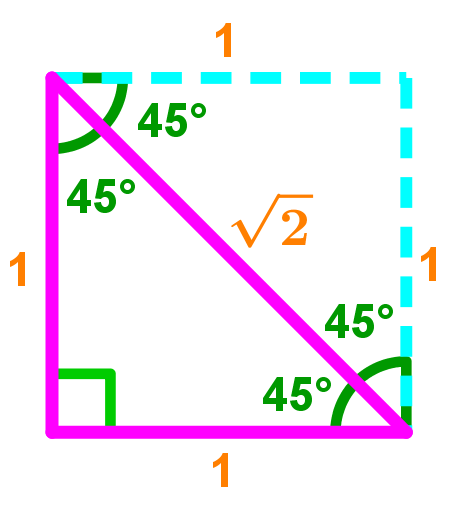
Looking at the image above, we can see that the reason why we are able to adapt the formula for calculating the area of a square is because a 45-45-90 right triangle makes up half the area of a square.
To calculate the area of a square, we typically use A=length×height. Since these dimensions are both equal in a square and in the case of 45-45-90 triangles, we can simplify this to A=s×s=s2.
Our final simplified formula however should be A=2s2 because a 45-45-90 right triangle only accounts for half the area of a square.
Use this 45 45 90 triangle calculator to check your work and examine more closely the special relationship between the dimensional ratios, perimeter and area of 45 45 90 triangles. This right triangle solver is just an aid so remember to practice on your own first!
Does a rhombus make 45-45-90 triangles?
Although the intersection of both diagonals in a rhombus can form 4 right angle triangles (see below), the other angles in these right angle triangles are not equal and are not necessarily 45°. In addition, these right angle triangles are not isosceles, so the length of the sides of the triangle (excluding the hypotenuse), are not equal. Therefore since these right angle triangles do not follow the same triangle angles of 45-45-90 triangles nor have side lengths that are in ratio of 1:1:2, a rhombus does not make 45-45-90 triangles.
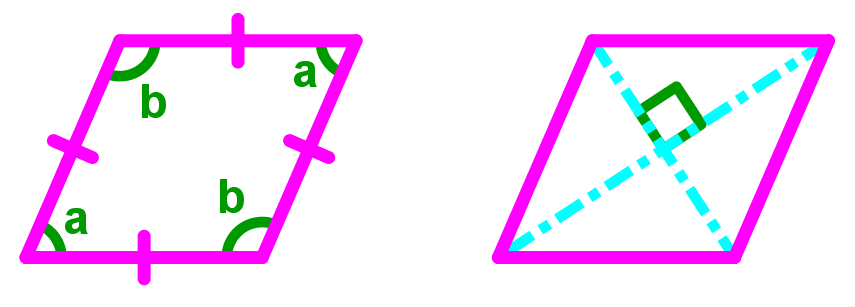
Use this interactive tool to examine the different properties of different rhombuses.
Walk through Example and Practice with 45 45 90 triangles
Before we go through an example, here are some of tips to help you when solving 45 45 90 triangles trigonometry questions:
1. If a trig question is asking for the answer to be in "exact value" form, this is likely going to require the use of a special triangle. This may be a 45 45 90 triangle of perhaps a 30 60 90 triangle. Recall that with special triangle trigonometry, we do not have to round or use decimals due to the unique ratios between the lengths of the sides. However, always remember to simplify your answer by rationalizing the denominator, simplifying the radical or fraction.
2. Commit to memory the ratios between the length of sides in 45 45 90 triangles – 1:1:2. An easy way to remember this ratio is that since you have two angles that are equivalent (i.e. 45°, 45°), the length/ratio of two sides should also be equivalent.
3. Another memory aid to keep handy is SOHCAHTOA. While we may know the basic ratio of the length of sides in 45 45 90 triangles, we need to also know how to use this information and how to plug in values into the right trig formula.
Example 1:
-
Step 1. Rewrite the equation – do not be confused by the expression "sin2"
3(sinθ)2=3(sin45)2 -
Step 2. Draw the special 45 45 90 right triangle and identify what the trig function is saying. In this case for "sin 45", the sine function and corresponding rule we follow is SOH, i.e. sin=hypotenuseopposite

Example 1. 45-45-90 special right triangle depicting special ratios and angles -
Step 3. Substitute in your values obtained from using the appropriate trig formula and simplify. Remember that the question is asking for exact values, so you can leave your answer as a fraction in this case.
Feeling confident with 45 45 90 special right triangles yet? Let us explore more special right angle triangles together and practice more right triangle trigonometry! Another type of special right angle triangle you will commonly encounter in trigonometry are 30 60 90 special triangles.
Basic Concepts
remaining today
remaining today



