Reduction of order
All You Need in One PlaceEverything you need for better marks in primary, GCSE, and A-level classes. | Learn with ConfidenceWe’ve mastered the UK’s national curriculum so you can study with confidence. | Instant and Unlimited Help24/7 access to the best tips, walkthroughs, and practice questions. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
Examples
Lessons
- Using Reduction of Order
Find the general solution to the following homogeneous linear second order differential equation:
xy′′+y′=0
Where it is known that y1(x)=c~1 is a solution
Where c~1 is a constant. - Find the particular solution to the following homogeneous linear second order differential equation:
x2y′′−xy′+y=0
Where it is known that y1(x)=x is a solution. The initial values are y(1)=2, and y′(1)=1
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Reduction of Order
The method of reduction of order to solve a second order differential equation is based on the idea of solving first order differential equations one after the other which have been derived from the original second order equation to simplify the problem. The name of this method comes exactly from this procedure, since we can literally say that by solving first order differential equations to find the solution of the problem we "reduced" the order of the original equation.
Once we have a set of first order differential equations to solve the problem, we can work through them using simpler approaches such as the method of separable equations or the Bernoulli equation, etc. Whichever approach is selected depends on the set of equations you are left to solve with, throughout this article we will go ahead and solve a few different examples to show the step by step methodology.
As mentioned before, we will be solving second order differential equations by the reduction of order technique, if you are not familiarized with these type of equations yet or if you need a quick review on the topic, we recommend you to visit the section on homogeneous linear second order differential equations in the StudyPug website before you continue with this topic.
Back to the main question for this article, how does the method of reduction of order actually transforms the original second order differential equation into a simpler one? In truth, for us to be able to work through this method we should already know one of the solutions to the original differential equation so we can find a second solution, this second solution does not need to be proportional to the solution given, or in other words, the second solution can be linearly independent, which is usually the desired case.
Solving second order linear differential equations
Generally an example containing a homogeneous second order linear differential equation of the form:
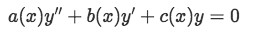
Will have two solutions named:
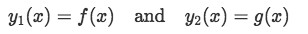
And the general solution will be of the form:
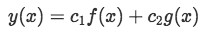
For cases like this, a problem given will contain equation 1 with its defined functions of a(x), b(x) and c(x), along with the first solution y1 already defined. The second order differential equation then will be solved by being reduced to a first order differential equation, combined and moved around along the equation for the first solution by using basic calculus and often solely algebraic methodology, such as simple substitution, so the second solution can be found. For an introduction example including the step by step explanation on how to find the general solution of a homogeneous linear second order differential equation where the first defined solution is a constant, please check out our videos at the top of this article at the StudyPug website in its section "Reduction of Order".
Now all this may seem a little confusing in words, therefore, to make this point clearer let us take a look at the next example where we use the method of reduction of order to find a second solution of the differential equation: In this case, we will find the particular solution to the following homogeneous linear second order differential equation:
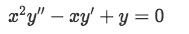
Where it is known that y1(x)=x is a solution and the initial values are y(1)=2 and y'(1)=1. Now we are going to find the second solution y(x), which we empirically know should be in the form y(x)=v(x)x=vx, by converting the original problem into a first order equation.
The reason why the second solution takes the form of v*x automatically comes from our easiest guess, which implies that the second solution should be related in some way to the first one, thus in this case we select to have a random function of x (which we call v(x)) to multiply our first solution, giving us a conventional form on how this second solution should look like. Our task here will be to find what v(x) is.
By utilizing this method, our second solution will usually be a complete general solution of the second order differential equation which will include our first solution. Because of that, although the manipulation can get lengthy, it is one of the best methods to obtain a final solution to the differential equation. In this case, the problem will be explained step by step, and most of these steps (or a simple modification of them) can be re-followed for other examples with second order homogeneous differential equations where a solution and parameters are known.
-
Step one: For this problem, we start the manipulation by obtaining the first and second derivation of our second solution in its guessed form.
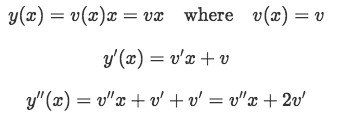
Equation 4(a): First and second derivation of our second solution Now we substitute these derivations into our second order differential equation, since we want them to be a solution of it, so our differential equation goes from:
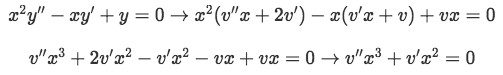
Equation 4(b): Substituting the values found for the derivations into our second solution Notice we factorized the x's in and computed vanishing terms to obtain the simplest form of the equation.
-
Step two: We convert the second order differential equation into a first order differential equation easier to solve, by substituting v'=w and v''=w'.

Equation 4(c): Converting from second order to a first order differential equation We solve this new equation by separation method:
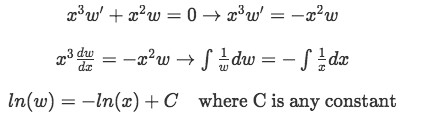
Equation 4(d): Solving by separable equations The results for these integrals were obtained assuming both w and x are bigger than zero.
Applying the exponential to both sides we obtain the final answer for w:

Equation 4(d-1): Final value of w where C1 is also any constant value, this constant is the new name we put to eC=C1
-
Step three: Having found w, we obtain the value of v(x) by computing the antiderivative of w.
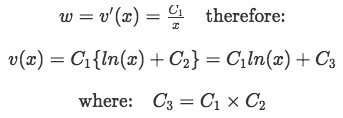
Equation 4(e): Obtaining the value of v(x) Since the constants are all any numbers, for simplicity we will equal them all to 1 and we obtain:
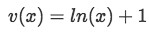
Equation 4(e-1): Simplified value of v(x) And so our second solution is:

Equation 4(f): Second solution of y in its general form Notice this is a general solution containing y1(x)=x of the form:
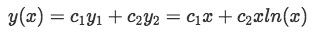
Equation 4(g): General solution of y containing the first solution Where y2(x)=xln(x) and c1 and c2 are two new constants we need to find.
-
Step four: To find the particular solution to the original homogeneous linear second order differential equation we input the initial parameters y(1)=2 and y'(1)=1.
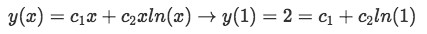
Equation 4(h): Inputting the initial conditions to find a particular solution to the differential equation We know that by definition ln(1)=0
And so the second term in the equation vanishes and we are left with: c1=2
Now we get the first derivative of y to use the second parameter:
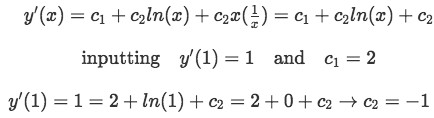
Equation 4(h-1): Inputting the initial condition to to the first derivative of y, to find a particular solution to the differential equation Therefore the final general solution of the second order homogenous differential equation is:
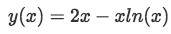
Equation 4(i): Final general solution to the second order homogeneous differential equation
To summarize the steps followed, let us list them with a small description of each. You can come back to this step list while you work through other problems with the method of reduction of order.
- Obtain the first and second derivation of the second solution in its guessed form. Then substitute these into the original second order differential equation we want to solve.
- We convert the second order differential equation into a first order differential equation by substituting v'=w and v''=w'. Then solve the first order equation using simpler methods such as separation to obtain the value of w.
- Obtain the value of v(x) by computing the antiderivative of w. Substitute this into the guessed form of the second solution to form a general solution of the second order differential equation.
- Find the particular solution of the problem by inputting the initial conditions (or parameters) given in the problem.
As you may have realized by now, there is not a unique reduction of order formula that works for every scenario, so the reduction order method is actually a combination of methods we already know on how to solve first order differential equations along with new tricks on our bag about differentiation, knowledge on the types of second order differential equations we have at hand, and some know-how or skill, which one develops through practice.
Reduction of order examples
As mentioned before, in order to solve reduction of order problems one has to develop certain empirical skill if you will, and for that, we will go through another example where we will follow the steps we listed on top. You will notice that although the main instructions are there, for every different example you will face challenges to solve on your own.
The main purpose of this example is for you to see the logic behind the proposed steps of solution, and at the end, you will be provided with a way to check if your solution is correct. Also a little reminder, we recommend you make sure to understand every step of the problems on this article so you can come back to them later to practice and even use them as reference later in your studies.
So here comes the final example, having the following homogeneous linear second order differential equation:
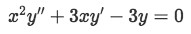
for x>0 and y1(x)=x with initial conditions: y(1)=3 and y'(1)=3/2
-
Step one: We can fairly assume the solution will have the form y(x)=v(x)×x=vx so we obtain its first and second derivative:
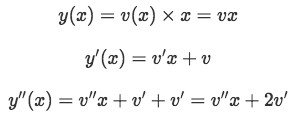
Equation 5(a): First and second derivation of our second solution Then we substitute these three equations into the original second order differential equation:
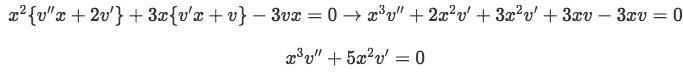
Equation 5(b): Substituting the values found for the derivations into our second solution Notice that in the last part of the equation the terms containing v cancel each other, usually this will be the case facilitating us the next step. So our equation has been simplified and we can convert it into a first order differential equation in the next step.
-
Step two: Let us make the substitution of v'=w and v''=w' in order to convert the second order differential equation into a first order differential equation.
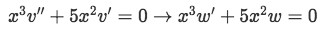
Equation 5(c): Converting from second order to a first order differential equation Now we solve for w by separation:
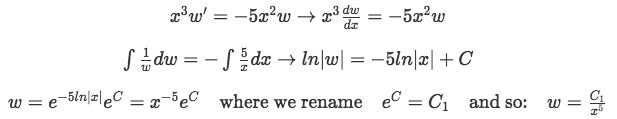
Equation 5(d): Solving by separable equations Remember C is just a constant and so we rename it.
At this point you will be seeing constants popping up every now and then, remember that these are just random numbers that we do not know, and therefore we cannot do anymore but name them to keep them in our operations. In some examples you can just simplify the equations by assuming all constants have a value of 1 (just like we have done before in this article), this can be done since the proportionality relationship remains even if you assign a value to these constants. In this example it is convenient to leave the constants just as they are, so we continue with them, naming and renaming them as they continue to transform throughout our operations, but keep in mind, every time you see a C in the operations with a new sub-index, it just means that either a new constant has come up or we have changed the name of one we already had due the operations it has gone through. We will be solving for these constants at the end.
-
Step three: Obtain the value of v(x) by computing the antiderivative of w.
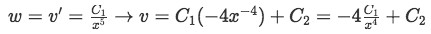
Equation 5(e): Obtaining the value of v(x) We substitute this into y(x)=vx
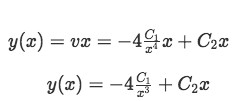
This is a general solution of the second order differential equation of the form: y(x)=c1y1+c2y2
Clarification:
Notice that in our solution the constants are written with uppercase "C" while in this last equation the names of the constants are in lowercase "c". The reason is that the formula containing the lowercase constants is just the conventional formula we use to denote the general solution of ANY homogeneous linear second order differential equation. Therefore, these lowercase "c"s are not the same constants we have found in our solution of y. Our uppercase "C's" are our particular solution constants to solve for in this example.
-
Step four: Now we can finally find the particular solution of the problem simply by inputting the initial conditions given. In this case:
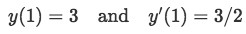
Equation 5(g): Initial conditions for the differential equation Therefore we obtain the first derivative of our solution equation and apply the conditions:
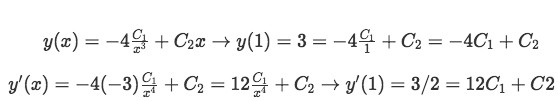
Equation 5(h): Inputting the initial conditions to find a particular solution to the differential equation So having the two equations:
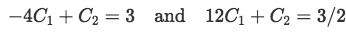
Equation 5(h-1): Two equations for two unknowns to find the values of the unknown constants We solve for the two constants using basic algebra:

Equation 5(h-2): Finding the values of the two unknown constants Substituting this into our general solution we obtain:
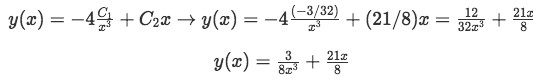
Equation 5(i): Final solution to the second order homogeneous differential equation
You can go back on your own and prove that this solution is correct.
In case you are not sure how to do this, the basic steps for the proof are to find the first and second derivative of your solution, and then plug it into the original second order differential equation. Once you have simplified as much as possible all of the terms in the equation, you will notice how all of them are going to cancel each other, since the whole equation is zero. Let us do this so you can see how it is done and can recreate it for future problems on your own:
Proof:
-
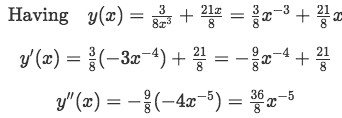
Equation 6: Obtaining the derivatives of the found expression of y to prove the solution to the differential equation -
Substituting this into equation 5:

Equation 7: Substituting the values found in equation 6, into equation 5 -
As you can see, the third and fifth terms cancel right away leaving:
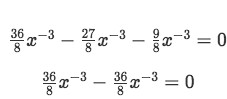
Equation 8: The solution found for the differential equation is correct, since reverse engineering produces the same answer So the answer we obtained for the second order differential equation is CORRECT!
If in any other case while you are practicing on your own, your solution does not resolve the original second order differential equation while going through the proof, then you need to start over solving for the differential equation and see where the error started. Do not get discouraged if this happens, remember, is all about practice, and you will get the hang of it in no time.
Notice that in this article we have focused on solving homogeneous second order linear differential equations, but you can also use the method of reduction of order to solve a nonhomogeneous differential equation. We will leave that discussion for other section. For now, the main purpose is for you to get acquainted with the method and understand that there are not reduction of order differential equations which will magically give you the response, is all about the mathematical manipulation of the information and the knowledge/skills we already have.
For examples using this and other methods while solving second order differential equations on physical problems, visit the section on applications of second order differential equations, where you will find a meaningful approach to differential equations' problems by looking at how useful these mathematical expressions and techniques are on our gradual understanding of the world and the development of technology.
We also recommend to take a look at the next differential equations notes and example on the reduction of order technique.
There will be two solution to the above differential equation:
y1(x)=f(x)
y2(x)=g(x)
And all general solutions will be of the form:
The method of Reduction of order assumes that one solution is already know (i.e. we know that y1(x)=f(x) is a solution the above differential equation) and uses a specific method to find another solution.
Note:
We will use interchangeably v(x)=v, and other shorthand notation of that form.
Steps to solve Reduction of Order problems:
1) Assume that your second solution is of the form y2(x)=v(x)f(x), where y1(x)=f(x) is the solution we know.
2) Find y2′, and y2′'
3) Insert y2,y2′, and y2′′ into a(x)y′′+b(x)y′+c(x)y=0
4) Get rid of the solution with y1(x)=f(x), and rearrange your equation to isolate v′ and v′′
5) Substitute w=v′, and w′=v′′
6) Solve for w in the new first order differential equation
7) Substitute w=v′ back in and then solve for v
8) The second solution to the differential equation is y2(x)=v(x)f(x), with the v found from the previous steps.
remaining today
remaining today



