Evaluating inverse trigonometric functions
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practise With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practise on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Understanding the Use of Inverse Trigonometric Functions
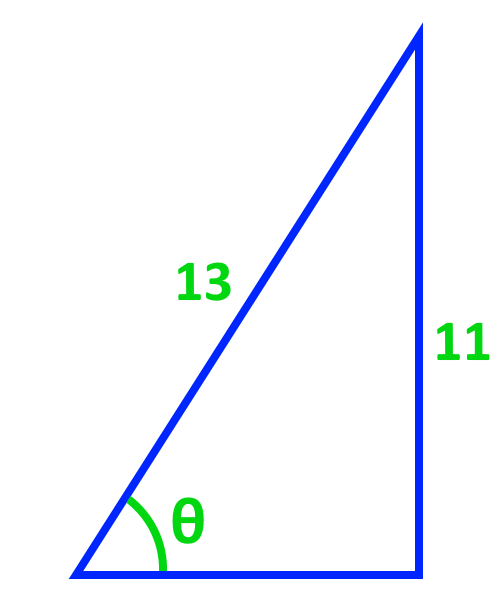
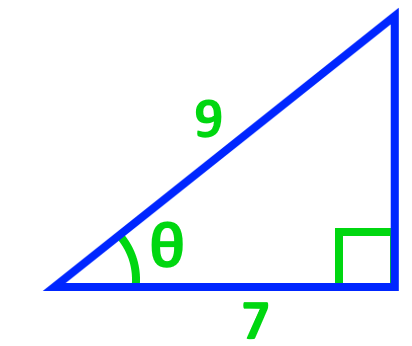
Find the angles for each of the following diagrams.
Find the angle for the following isosceles triangle.
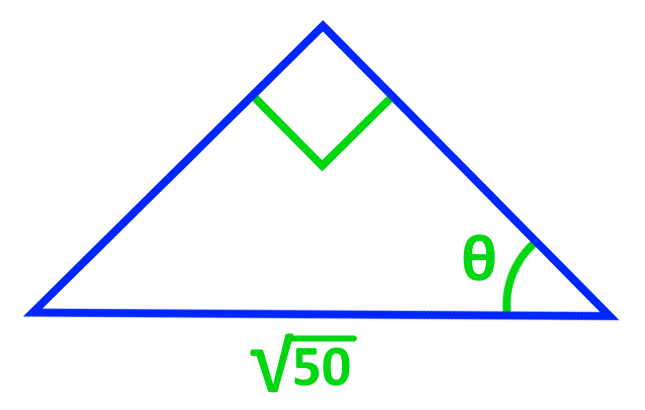
- Determining the Angles in Exact Values by Using Special Triangles
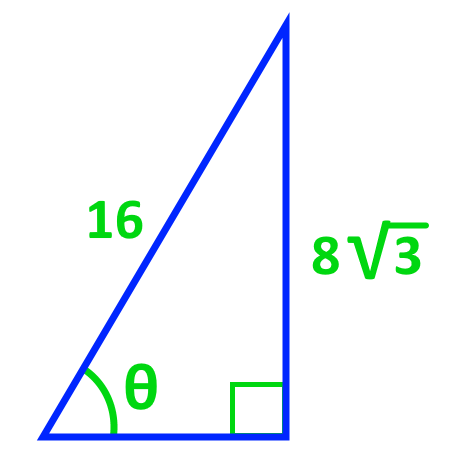
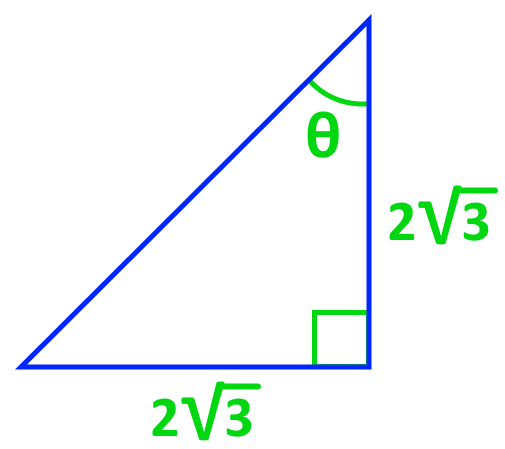
Find the angles for each of the following diagrams in exact value.
- Application of the Cancellation Laws
Solve the following inverse trigonometric functions:
- Solving Expressions With One Inverse Trigonometry
Solve the following inverse trigonometric functions:
- Evaluating Expressions With a Combination of Inverse and Non-Inverse Trigonometry
Solve the following inverse trigonometric functions:
- Special Cases: Evaluating Functions With Numbers Outside of the Restrictions
Solve the following inverse trigonometric functions: