Complex eigenvalues
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practise With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practise on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
- Complex Eigenvalues Overview:
- Review of Complex numbers
• The square root of -1
• Finding complex roots using the quadratic equation
• Re(v) and Im(v) of Complex vectors - Complex Eigenvalues and Eigenvectors
• The Characteristic Equation
• Using the quadratic formula to find the complex roots
• The corresponding eigenvectors - Finding the Argument
• Find the Eigenvalues a±bi
• Find the scale factor ∣λ∣=r=a2+b2
• Divide the scale factor of the matrix
• Compare with the rotational matrix
• Solve for the argument φ - The Formula A=PCP−1
• Get the Eigenvalue λ=a−bi and Eigenvector v
• Find Re(v) and Im(v)
• Combine them to get the invertible matrix P
• Use a and b from the eigenvalue a−bi to get matrix C
Examples
Lessons
- Finding the Complex Eigenvalues/Eigenvectors
Find the complex eigenvalues of A and their corresponding eigenvectors.
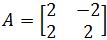
- Finding the Argument using Eigenvalues
The transformation x→Ax is the composition of a rotation and scaling. Find the eigenvalues of A. Then give the angle φ of the rotation, where −π < φ≤π, and give the scale factor r if
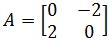
- The transformation x→Ax is the composition of a rotation and scaling. Find the eigenvalues of A. Then give the angle φ of the rotation, where −π < φ≤π, and give the scale factor r if
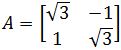
- Finding the Invertible Matrix and Matrix C
Find an invertible matrix P and a matrix C of the form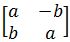 such that the given matrix has the form A=PCP−1 if
such that the given matrix has the form A=PCP−1 if
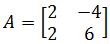
- Advanced Proofs Related to the Eigenvector
Let A be a real n×n matrix, and let x be a vector in Cn. Show that
Re(Ax)=A(Re x)
Im(Ax)=A(Im x) - Let A be a real 2×2 matrix with a complex eigenvalue λ=a−bi where b=0 and an associated eigenvector v in C2. Show that:
A(Re v)=aRev+bIm v
A(Im v)=−bRev+aIm v
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Complex Eigenvalues
What is an eigenvalue and how can it be complex?
Recalling from the lesson on eigenvalues and eigenvectors, we see again the eigenvalue definition with a little spin to include the characteristics that make it a complex equation for the cases studied on this lesson.
Given that an eigenvector is a non-zero characteristic vector (column vector) which changes by a constant factor when a square matrix is applied to it through matrix multiplication. We know that the constant characteristic factor, which scales the vector to be equal to the matrix multiplication, is what we call the eigenvalue of a matrix (usually denoted as λ).
For this lesson we will study the cases in which the eigenvalues of matrices happen to be a set of complex numbers: numbers containing a rean and an imaginary part thanks to a term containing the square root of minus one. In the next section we will see how to find such eigenvalues to them produce their proper eigenvectors.
How to find eigenvectors of a matrix
We will follow the same methodology as seen in past lessons to calculate eigenvalues and their corresponding eigenvectors, thus, in order to find the eigenvectors of a matrix we first have to compute its eigenvalues through the characteristic polynomial equation:
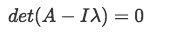
The determinant of the characteristic equation will produce an algebraic second degree expression for which we have to solve its roots. While solving the roots of such equation through the quadratic formula you will notice that the discriminant happens to be negative and so, the result of the quadratic equation will be a set of complex numbers.
From algebra we know that complex numbers originated in mathematics due to our need for an expression to write down quantities representing the square roots of negative numbers. How is that so? We have mentioned before that complex numbers contain a real part (real numbers) and and imaginary part (imaginary numbers), an imaginary number is any number which contains a multiplication of a real number and the imaginary unit, where this unit imaginary number is defined as the solution to the equation x2+1=0 or simply the square root of -1 and represented as i. Therefore, imaginary numbers arised from the need to represent and work with the square roots of negative numbers which do not exist in real numbers, and so, since they are not "real" they got called "imaginary".
And so, for this lesson we will be studying such cases in which the quadratic equation producing the roots, or in this case eigenvalues, will encounter the next conditions:
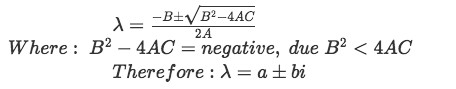
As done before in our past lesson, the main purpose of obtaining the eigenvalues of a matrix is to then produce the set of corresponding characteristic column vectors named the eigenvectors.
We know that for each eigenvalue there are corresponding eigenvectors. Their close relationship was described and explained in the past lesson as the multiplication of the matrix in question by the eigenvector which is equivalent to the product of the eigenvalues times the same vector, defined by the formula: Ax=λx, where Lambda represents one of the eigenvalues of matrix A, and x is its corresponding column characteristic vector, or eigenvector. Therefore, it is very easy to compute an eigenvector, one only has to solve for the vector in the equation:
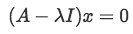
Where I is the identity matrix: a square diagonal matrix where all of the values of its main diagonal are equal to one. The zero in the right hand side of the equation represents the zero vector (a column vector with only zero values).
Remember that in this case x represents the eigenvector (a column vector) we will calculate for, and so, by following this method we usually obtain the same amount of eigenvectors as the amount of eigenvalues we found by using equations 1 and 2, and we have to solve this equation for each eigenvalue separately.
How to find eigenvectors of a 2x2 matrix? In short, when a matrix A is provided, the total list of steps to follow in order to compute the eigenvectors of the matrix coming from a resultant set of complex eigenvalues is as follows:
- Find the complex eigenvalues of a matrix using the characteristic equation described in equation 1
- Calculate the roots resulting from the determinant using the quadratic formula with the conditions shown in equation 2.
- Use the eigenvalues found in order to compute the eigenvectors through equation 3.
- Transform the original arrangement coming from equation 3 into an augmented matrix in order to solve for the vector v.
- You will need to use the row-reduction method in order to obtain the final column vector.
- Repeat step 2 for each eigenvalue we found in step 1, and so, produce at least the same amount of eigenvectors as eigenvalues found.
Finding eigenvectors from eigenvalues
Before entering full mode into the eigenvalue example exercises let is be said that the methods you will find below for calculating an eigenvalue or an eigenvector example, are the same, or very similar to the techniques and calculations done before in our past lesson. The trick here is to not forget we are obtaining and working with complex numbers, which can add a little bit of challenge for the details and all the algebraic rules they entail. This is of course nothing difficult to achieve, but is worth mentioning this lesson is more of a practice session reviewing what we have done before, with a little excitement added.
Example 1
Consider Matrix A found below. Find the eigenvalues using the formula to compute the characteristic polynomial of a matrix (equation 1).
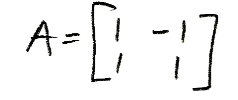
-
Now we use the characteristic polynomial equation to compute the determinant and come up with a quadratic equation in order to find all the possible values of λ (eigenvalues).
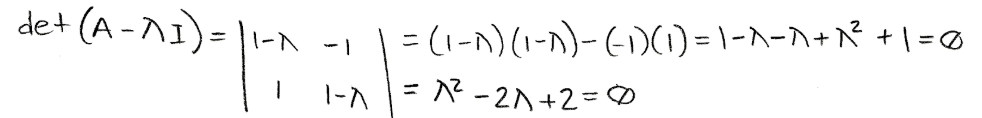
Equation for example 1(a): Solving the characteristic polynomial equation. -
Next, we use the quadratic formula to find the roots of the resultant equation (follow process shown in equation 2). These roots represent the eigenvalues of 2x2 matrix A.
And we are done finding the eigenvalues!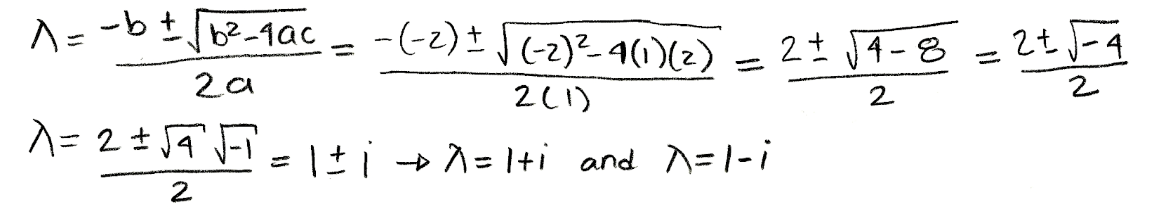
Equation for example 1(b): Calculating the eigenvalues
-
Since we are already solving for the characteristic elements of matrix A, let us follow through with this problem and calculate the corresponding eigenvectors. This is important since throughout your studies you will find out that problems will usually ask for both eigenvalues and eigenvectors to be calculated.
-
Let us calculate the corresponding eigenvector to the first eigenvalue. Thus, for λ=1+i :
(notice we have decided to call the vector "v" this time).
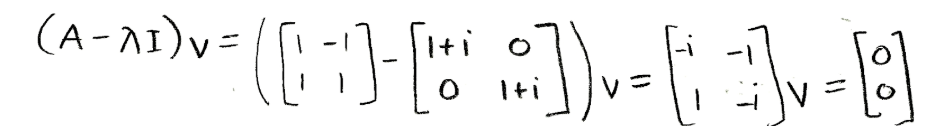
Equation for example 1(c): Solving for the first eigenvector (part 1) -
We use an augmented matrix and row reduction in order to obtain the set of linear equations to use while looking for the components of vector v:
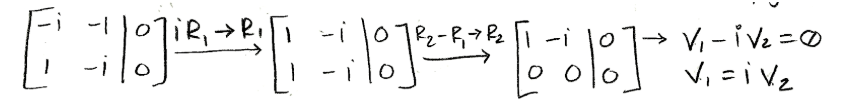
Equation for example 1(d): Solving for the first eigenvector (part 2) -
Notice how in the first row-reduction operation we multiplied the first row by its conjugate, make sure to pay close attention to this explained on the videos for the lesson.
Solving for the components, we can now find eigenvector v corresponding to the λ=1+i eigenvalue:
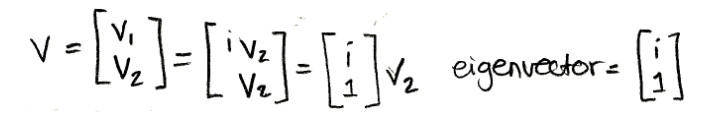
Equation for example 1(e): Solving for the first eigenvector (part 3) -
Now we repeat this same procedure in order to find the eigenvector corresponding to the second eigenvalue when λ=1+i :
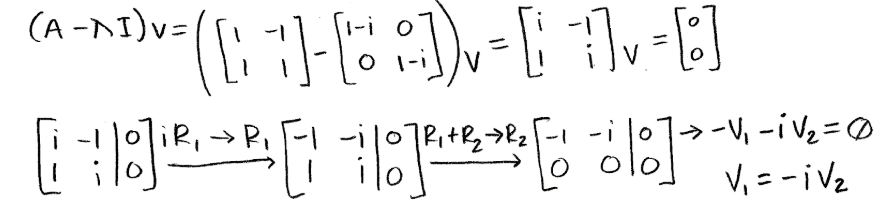
Equation for example 1(f): Solving for the second eigenvector (part 1) -
So we have used equation 3, in order to come up with the augmented matrix to solve for the components of the vector v in this case, now we are left to just put the eigenvector v together with the components found:
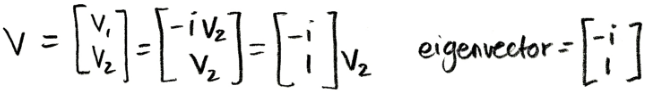
Equation for example 1(g): Solving for the second eigenvector (part 2)
And so, we have obtained the two corresponding eigenvectors for the two complex eigenvalues. Let us continue with more practice problems below!
Example 2
Find the eigenvalues of A:
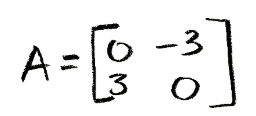
-
In order to find the argument, we first solve for the eigenvalues and eigenvectors of the matrix. Let us start doing it using equation 1 to find the eigenvalues first:
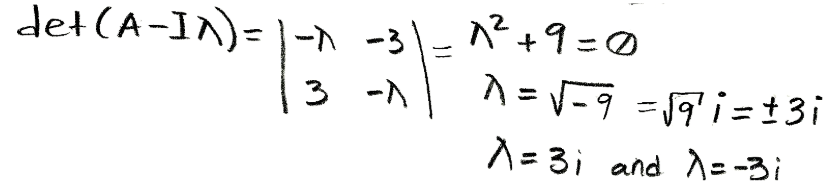
Equation for example 2(a): Solving the characteristic polynomial equation to find the eigenvalues -
Notice that for this problem it wasn't necessary to use the quadratic formula in order to find the values of the roots since the second degree algebraic equation resulting from the determinant was very simple. There is an important reminder for these kind of scenarios, whenever you solve for the roots of an equation which is as simple as the squared variable equal to a value, we know that the result will come up by just square rooting the quantity at hand. Some may be inclined to think there will be only one possible answer for this case, but whenever we take a square root of a number there will always be two possible answers: the positive and the negative numbers, which multiplied by themselves, result in the quantity inside the square root.
- And so, the eigenvalues are λ=3i and λ=-3i.
Example 3
Find an invertible matrix P and a matrix C of the form:
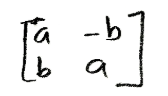
-
Such that the given matrix A has the form A=PCP−1 when A is as follows:
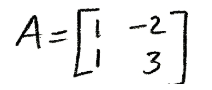
Equation for example 3(a): Matrix A -
Notice that this problem is asking for us to do a calculation very similar to those done in the diagonalization process. We will first find matrix C by computing the complex eigenvalues λ=a-bi
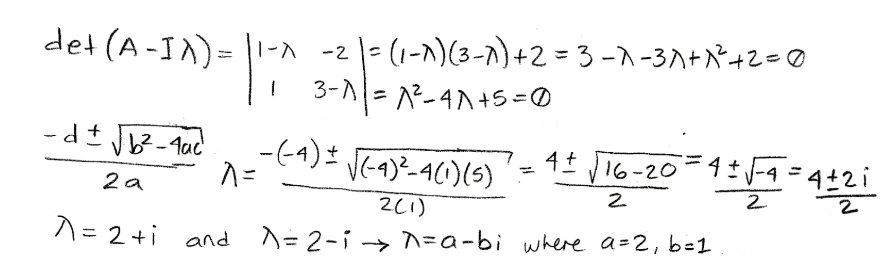
Equation for example 3(b): Obtaining the complex eigenvalues -
Using the complex eigenvectors found, we form matrix C:
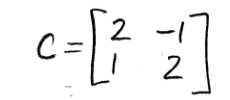
Equation for example 3(c): Matrix C -
In order to find the matrix P, and in consequence, knowing if it's possible to calculate its inverse, we need to calculate the eigenvectors associated to the complex eigenvalues found: For λ=a-bi
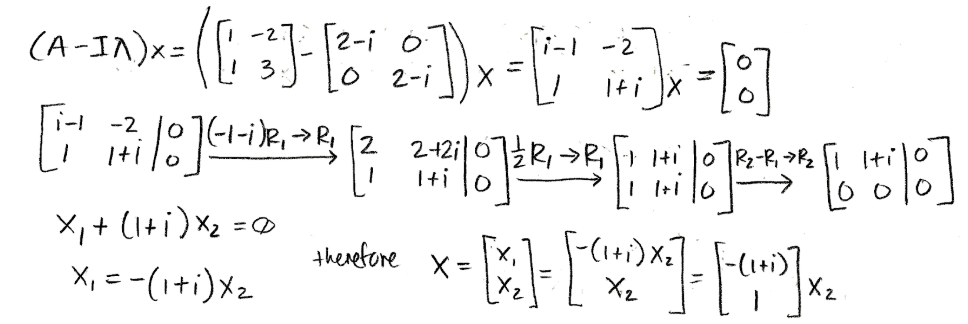
Equation for example 3(d): Computing the eigenvector (part 1) - Using the components found, we construct our eigenvector:
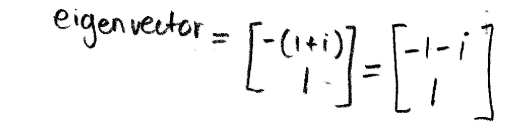
Equation for example 3(e): Computing the eigenvector (part 2) - Separating the real and imaginary parts of the eigenvector in a visual manner in order to use them to construct the matrix P:
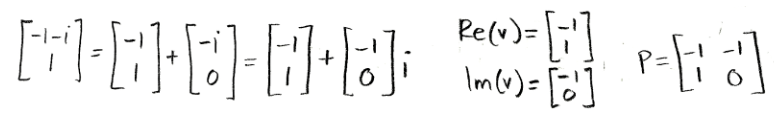
Equation for example 3(f): Computing matrix P - Notice that the general form for the eigenvalue equation in this problem contains a real part and an imaginary part, and so, we use these as the vectors which conform the matrix P.
At this point, we are done with this problem since we do not need to calculate the inverse of P and then go through the multiplication A=PCP−1 since is not asked for, but if you have time and would like to practice, we recommend you to go through the matrix multiplication and prove the results found on this lesson.
Example 4
Find the complex eigenvalues of A and their corresponding eigenvectors.
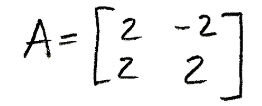
-
In order to find eigenvalues of 2x2 matrix A, our first step is to find the characteristic polynomial of the matrix:
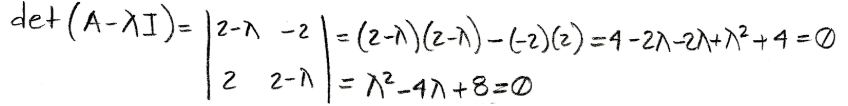
Equation for example 4(a): Calculating the characteristic polynomial of the matrix - And so, we use the quadratic formula to solve for the values of lambda:
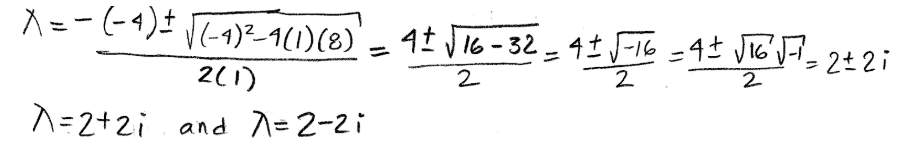
Equation for example 4(b): Finding the complex eigenvalues - Calculating the eigenvectors for λ=2+2i:
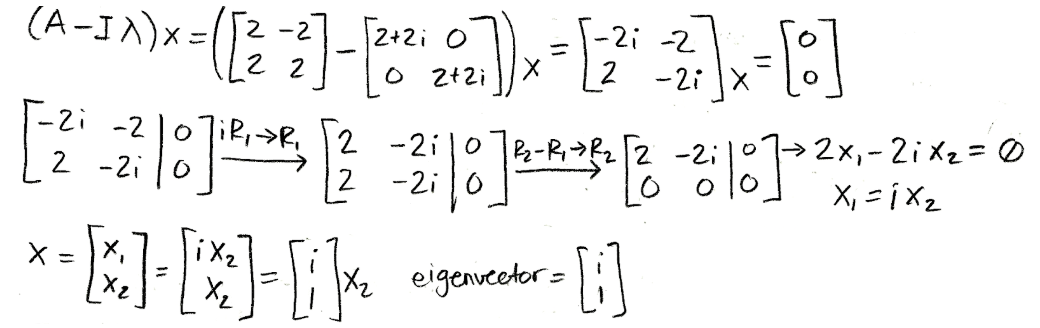
Equation for example 4(c): Calculating the corresponding first eigenvector - Following the same process to find the eigenvector for λ=2-2i:
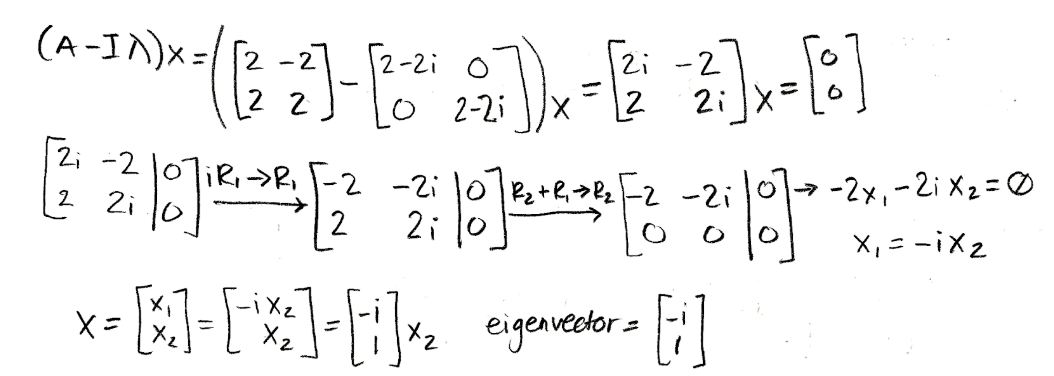
Equation for example 4(d): Calculating the corresponding second eigenvector
To finish up with our lesson we recommend you to continue your practice for calculating complex eigenvalues and eigenvectors by checking out these notes on differential equations or this interesting linear algebra lecture where you will find some in depth reading on our topic of today plus other examples to work with.
Given a complex vector
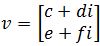 , the real part and imaginary part would be:
, the real part and imaginary part would be: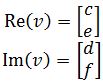
Let x→Ax be a transformation that is composed of scaling and rotation. Also, let
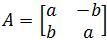 . Then we can find the angle (argument) φ in the complex plane by doing the following steps:
. Then we can find the angle (argument) φ in the complex plane by doing the following steps:1. Find the complex eigenvalues
2. Find the scale factor ∣λ∣=r=a2+b2
3. Divide the scale factor of the matrix
4. Compare with the rotational matrix
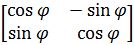 and create two equations
and create two equations5. Solve for the argument φ
Let A be a real 2×2 matrix with a complex eigenvalue λ=a−bi and associated eigenvector v in C2. Then A=PCP−1 where
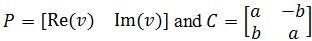
remaining today
remaining today



