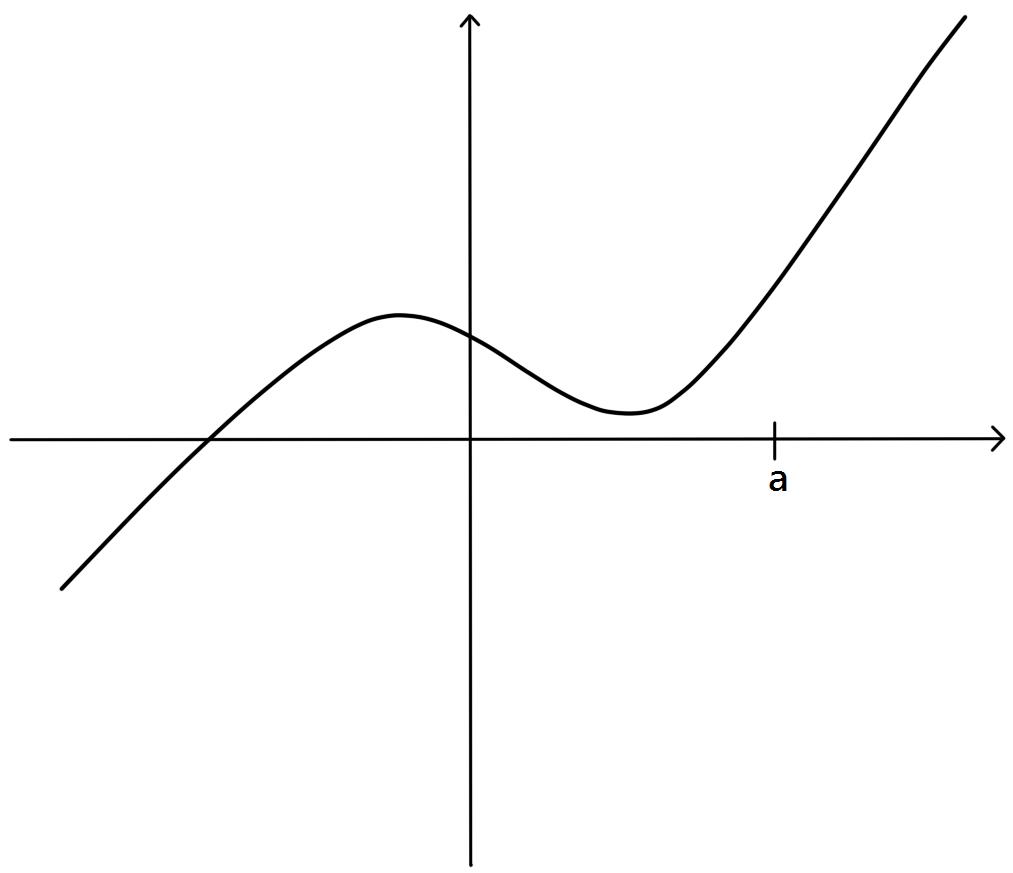
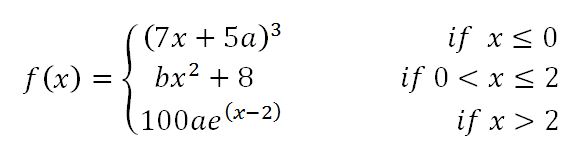Continuity
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practise With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practise on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/3
Intros
Lessons
- Introduction to Continuity
- Discuss CONTINUITY in everyday language: a function whose graph has no break in it.
- Discuss CONTINUITY in the context of Calculus:
A function is continuous at a number a, if:
Classify different types of discontinuities: removable VS. infinite VS. jump
Analyze: rational function with a hole:
VS. rational function with an asymptote:
VS. piecewise function:
- Lesson Overview - Continuity
0/4
Examples
Lessons
- Discussing "Continuity" Graphically
The graph of a function is shown below.- State the numbers at which is discontinuous.
- Explain and classify each discontinuity.
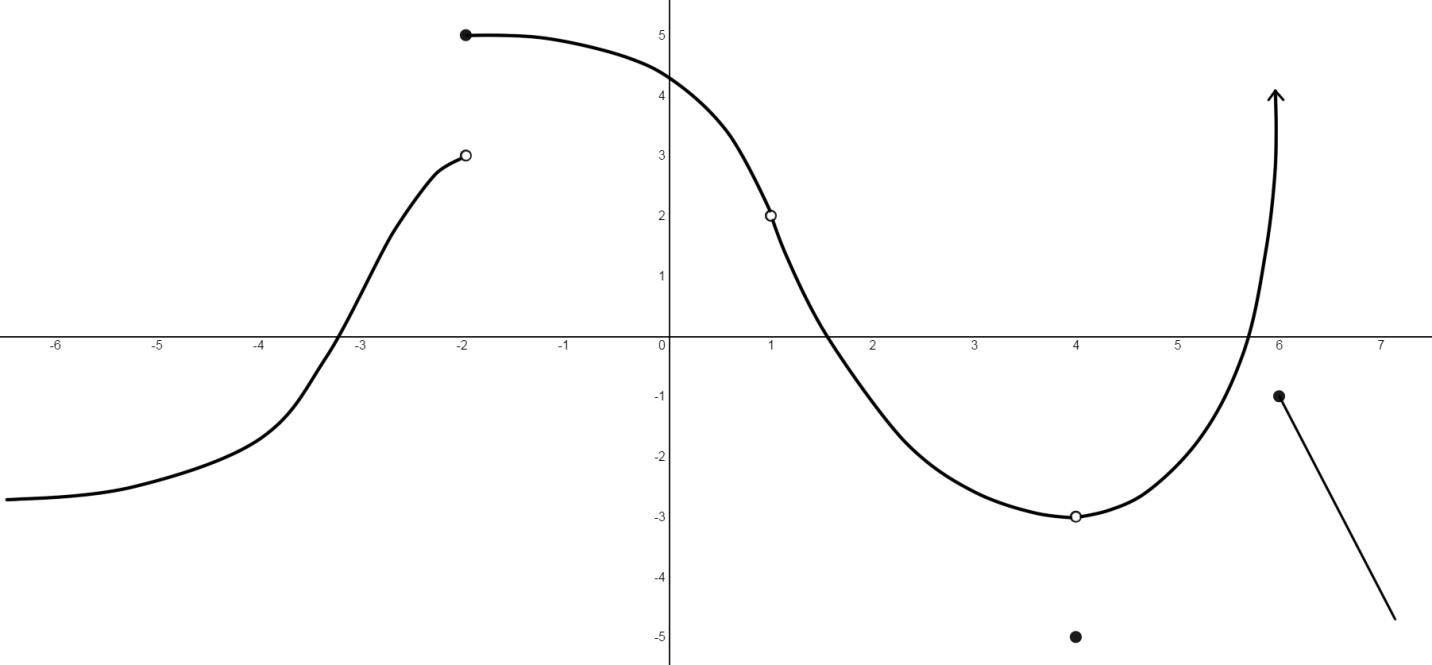
- Detecting Discontinuities
Are the following functions continuous at ?
i)
ii)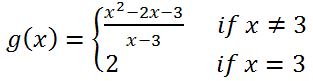
iii)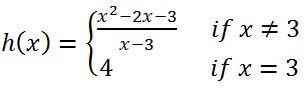
- Discontinuities of Rational Functions (denominator=0)
Locate and classify each discontinuity of the function: - Discussing "Continuity" Algebraically
Find the values of a and b that make the function continuous on (, ).