Related rates
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practise With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practise on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Examples
Lessons
- A 5-ft ladder is leaning against a wall. If the base of the ladder slides away from the wall at a rate of 2 ft/s, how fast is the top of the ladder sliding down the wall when the base of the ladder is 4 ft from the wall?
- Air is being pumped into a spherical balloon at a rate of 200cm3/s. How fast is the radius of the balloon increasing when the diameter is 1 m.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Related Rates
One of the hardest calculus problems that students have trouble with are related rates problems. This is because each application question has a different approach in solving the problem, and requires the application of derivatives. However once you know these 6 steps, then you should be able to solve any Calculus related rates problems you like.
How to Solve Related Rates
Here are the following steps in solving a related rates question:
1. If possible, draw a diagram to help visualize the problem.
2. Express the given information and rates (look for units with time in the denominator)
3. Express the asking rate (look for phrases such as "how fast", "at what", "find the rate", etc).
4. Write an equation that relates the various quantities of the problem.
5. Differentiate both sides of the equation, with respect to time, using the Chain rule.
6. Substitute the given information into the differential equation and solve for the asking rate.
Let's take a look at a few Calculus practice problems using these steps.
Related rates examples
Let's take a look at a related rates cone problem.
Question 1: A cone is 30 cm tall, and has a radius of 5 cm. Initially it is full of water, but the water level falls at a constant rate of 1cm per second. At what rate is the water draining from the cone?
Step 1:
We know that the cone is full of water, but the water is draining. So if we were to draw a picture, then it would look something like this:
Graph 1: Related rates cone picture - Step 2:
We are given information about the size of the cylinder, and the rate in which the water is draining.What is the rate constant of height? Well when the water is draining, the water level is going to change per second. This means the height is also going to change per second. Thus, expressing the given information and rate constant gives us:
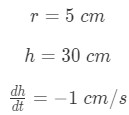
Equation 1: related rates cone problem pt.1 The reason why the rate of change of the height is negative is because water level is decreasing. Also, note that the rate of change of height is constant, so we call it a rate constant.
- Step 3:
The asking rate is basically what the question is asking for. In this case, it is asking for the rate which the water is draining from the cone. In other words, they are asking for the rate of change for the volume of the water. This leads us to write

Equation 1: related rates cone problem pt.2 - Step 4:
Since we are dealing with volumes and cones, it would be wise to use the formula for the volume of a cone.

Equation 1: related rates cone problem pt.3 - Step 5:
Taking the derivative of volume of a cone, we need to use the product rule and chain rule. First visualize the two products to be:

Equation 1: related rates cone problem pt.4 Now doing the product rule and chain rule gives:
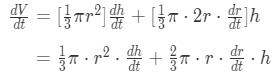
Equation 1: related rates cone problem pt.5 However, there is a problem here. We don't know what exactly dtdr is. So we have to figure out a way to get rid of this. We can do this by going back to the original equation,

Equation 1: related rates cone problem pt.6 If we can find a way to get rid of the variable r, then we can avoid getting dtdr when we take the derivative. But how does one get rid of the variable? By expressing r in terms of h. We can do this by using similar triangles. Notice that in our diagram from step 1, we can write more information about it.
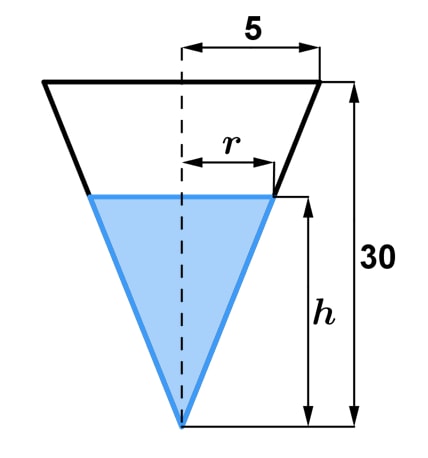
Graph 2: related rates cone 2D Notice the two triangles created from this drawing. Since the two triangles are "similar", then their ratios must be the same as well. In other words, the similar triangles formula gives:
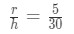
Equation 1: related rates cone problem pt.7 Isolating for r gives us:
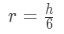
Equation 1: related rates cone problem pt.8 We just created an equation of r in terms of h using similar triangles! Now if we take this equation and substitute the r in the volume of a cone equation, then we will get:
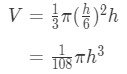
Equation 1: related rates cone problem pt.9 Now taking the derivative of this will give us:
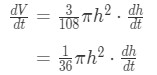
Equation 1: related rates cone problem pt.10 - Step 6:
Plugging in all the information we have to the differential equation give us:
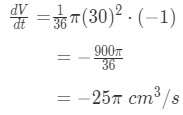
Equation 1: related rates cone problem pt.11 Hence the rate at which the water is draining from the cone is 25πcm3 per second.
Now let's take a look at another calculus problem. This one deals with a sliding ladder on a wall.
Question 2: A 12 ft ladder is resting against a wall. The distance between the floor and the top of the ladder is 6 ft. If the ladder is sliding down the wall at a rate of 2 ft per second, then how fast is the ladder moving away from the wall horizontally?
Step 1:
We see that the ladder is resting on a wall. Assuming that there is a floor, the picture would be: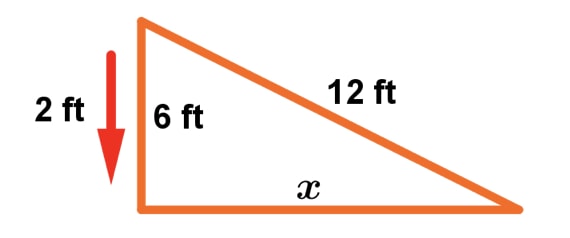
Graph 3: related rates ladder picture - Step 2:
We are given information about the size of the ladder, and the vertical distance between the ladder and the floor. We also know the rate at which the ladder is sliding down the wall. This is important because it tells us that the distance between the ladder and the floor decreases as the ladder is down the wall. In other words,
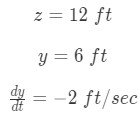
Equation 2: related rates ladder problem pt.1 However, do we know the horizontal distance between the ladder and the wall (the variable x)? We don't but we can calculate this using Pythagoras. Notice that:
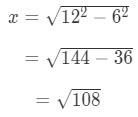
Equation 2: related rates ladder problem pt.2 Also, do we know the rate of the ladder (dtdz)? We actually do, we just need to think about. Can a ladder physically expand or shrink? No way! So in a sense, the rate of the ladder increasing or decreasing is 0 because the length of the ladder is never going to change. Hence,
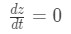
Equation 2: related rates ladder problem pt.3 - Step 3:
Again, the asking rate is what the question is asking for. In this case, it's asking for the rate of change in which the ladder is moving away from the wall. That is the rate of change of the horizontal distance (dtdx). So
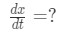
Equation 2: related rates ladder problem pt.4 - Step 4:
Since the picture we drew was a triangle, we probably want to use the formula of Pythagoras theorem.
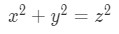
Equation 2: related rates ladder problem pt.5 - Step 5:
Using implicit differentiation and chain rule to take the derivative gives us:
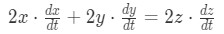
Equation 2: related rates ladder problem pt.6 - Step 6:
Plugging everything that we have found into the formula gives us:
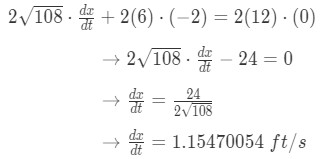
Equation 2: related rates ladder problem pt.7
Let's look at another related rates practice problems which involves a person walking away from a light pole. This is a pretty famous related rates shadow problem!
Question 3: A person is standing near a light pole. The pole is 30 ft tall and the person is 5 feet tall. The person walking away from the light pole at 21 ft per second creates a shadow behind her. At what rate is the length of the shadowing increasing when the person is 20 ft away from the pole?
Step 1:
First let's draw a picture and label some variables.Let us call the distance between the person and the light pole, the length of the shadow, and the length of the pole Also, note that dtdx is the rate at which the person is walking away from the pole.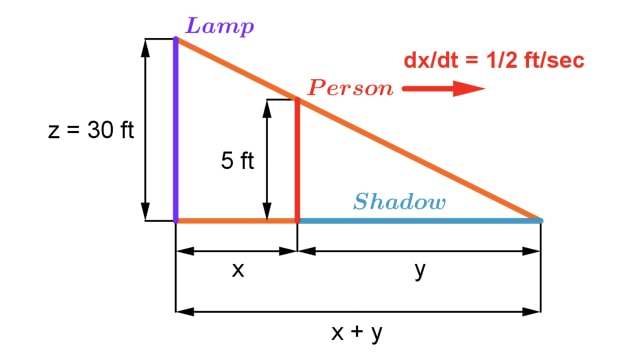
Graph 4: related rates person walking away - Step 2:
We are given that:
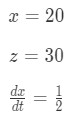
Equation 3: related rates light pole problem pt.1 We could also identify the hypotenuse of the triangle, but that would be meaningless in this question.
- Step 3:
Since we are looking at the rate at which the length of the shadowing increasing, then we are looking for dtdy. In other words,
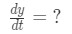
Equation 3: related rates light pole problem pt.2 - Step 4:
Many would be tempted to use the Pythagoras Theorem formula, however we see two triangles. In fact, we could see that the two triangles are similar, so it would be wise to use similar triangles here. Note that the ratio of the legs of the big triangle and the small triangle should be the same. In other words,
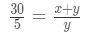
Equation 3: related rates light pole problem pt.3 - Step 5:
Even though the steps say to differentiate both sides of the equation, we first want to make the equation look nicer. Note that:
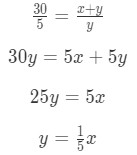
Equation 3: related rates light pole problem pt.4 Now differentiating both sides give:
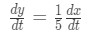
Equation 3: related rates light pole problem pt.5 - Step 6:
Plugging everything that we have found into the formula gives us:

Equation 3: related rates light pole problem pt.6 So the rate at which the shadow is increasing is 101 ft/sec.
Let's take a look at more hard calculus problems! This is one of the most famous related rates word problems that students encounter in the course. It involves a clock!
Question 4: The minute hand of a clock is 10 mm long, and the hour hand is 5 mm. How fast is the distance between the hour hand and the minute hand changing at 3 pm?
Step 1:
Imagine the clock at 4pm exactly and draw it out.Let d be the distance between the hour hand and minute hand.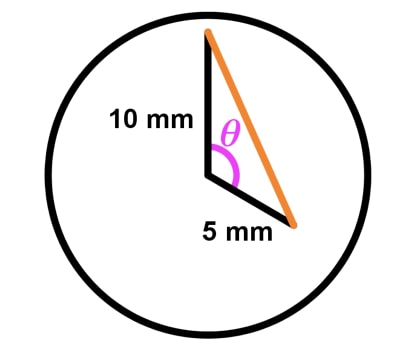
Graph 5: related rates clock picture - Step 2:
We are given information that the minute hand is 10 mm long and the hour hand is 5 mm. In other words,
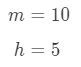
Equation 4: related rates clock problem pt.1 However, are we given the angle and the rate at which the angle is increasing/decreasing? No, but we can find those. Notice that the angle around the clock is 2π. If we were to divide this by 12, then that will be the angle difference between each hour. Hence,

Equation 4: related rates clock problem pt.2 Note that the minute hand is at 12 and the hour hand is at 4. That means the angle between them in terms of time is 4 hours. Hence multiplying the angle we found by 4 will give us the angle of the triangle we drew above.
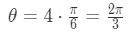
Equation 4: related rates clock problem pt.3 Now how do we find the rate at which the angle is increasing/decreasing? Well the minute hand does a full turn around the clock in 1 hour. We also know that the angle around the clock is 2π radians. So it must be true that
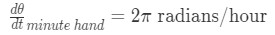
Equation 4: related rates clock problem pt.4 Where t is in minutes.
In addition, the hour hand takes 12 hours to do a full turn around the clock. Hence
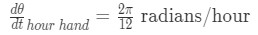
Equation 4: related rates clock problem pt.5 Now if we were to subtract them, then we will get the difference of the rates of two angles. This gives us the rate of the angle of the triangle in the picture.
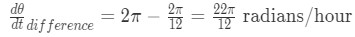
Equation 4: related rates clock problem pt.6 However, the minute hand is catching up to the hour hand, so it is actually decreasing the angle. So we actually have to put a negative in the rate of change of our angle. Thus,

Equation 4: related rates clock problem pt.7 - Step 3:
The asking rate is the rate at which the distance between the hour hand and minute hand is decreasing. In other words we are looking for:
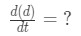
Equation 4: related rates clock problem pt.8 - Step 4:
Again, people would be tempted to use Pythagoras Theorem here. However, we are dealing with a triangle that is not always 90 degrees. Hence, we would want to use a formula that works for any triangle. The perfect formula for this would be the law of cosines. Note that the law of cosines formula for this triangle is:
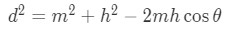
Equation 4: related rates clock problem pt.9 m and h are constant and never changes, so we can go ahead and plug those in.
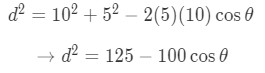
Equation 4: related rates clock problem pt.10 One thing to note here is that this formula gives us find d. Recall that:
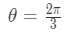
Equation 4: related rates clock problem pt.11 So that means
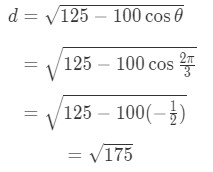
Equation 4: related rates clock problem pt.12 - Step 5:
Differentiating both sides of this law of cosines equation gives us:
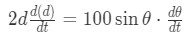
Equation 4: related rates clock problem pt.13 - Step 6:
Plugging everything into the formula we get:

Equation 4: related rates clock problem pt.14 If you want it at minmm instead, you could divide by 60, giving:
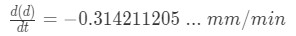
Equation 4: related rates clock problem pt.15
We have pretty much covered the most relevant questions for calculus related rates. Of course, there are many other questions for related rates calculus. However, as long as you follow the 6 steps, you should be able to do any question you like. If you want more practice problems, then I recommend you take a look at this link.
http://tutorial.math.lamar.edu/Classes/CalcI/RelatedRates.aspx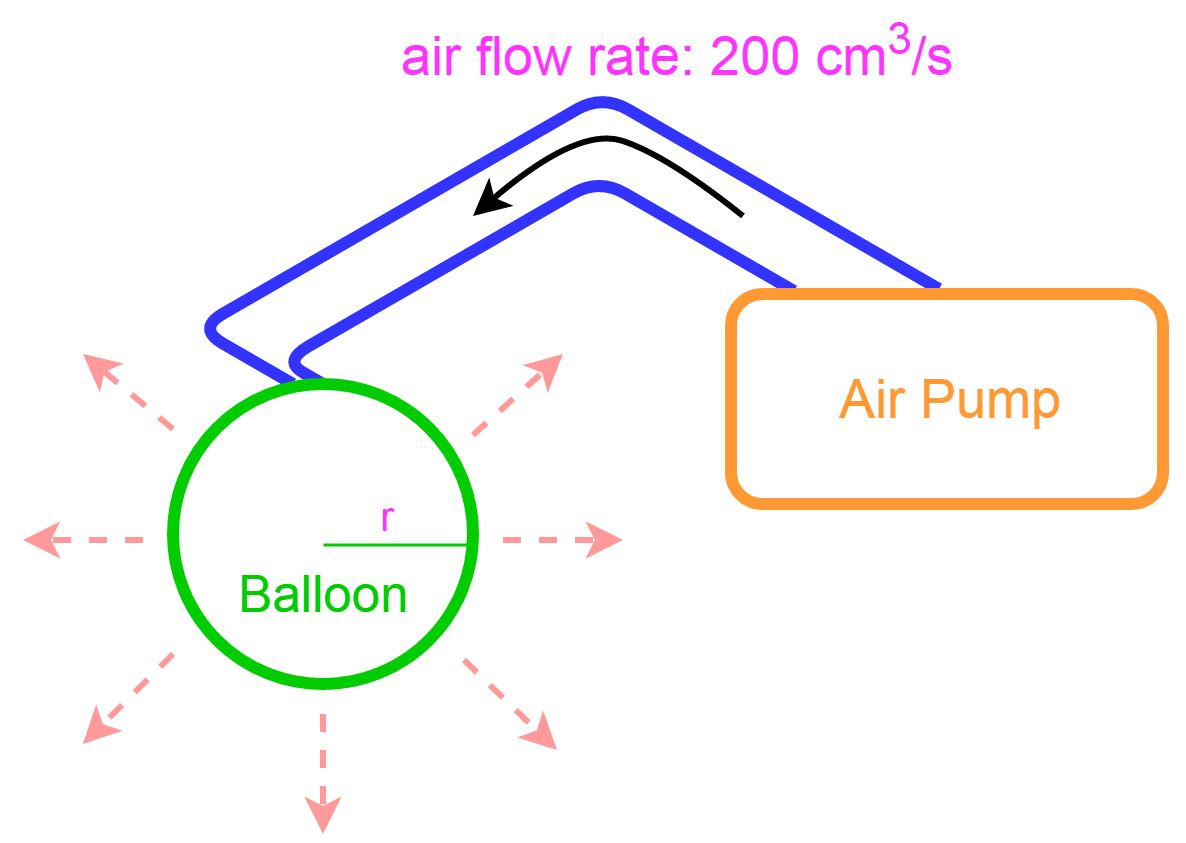 Note: Problem Solving Strategy
1. If possible, draw a diagram to help visualize the problem.
2. Express the given rates (look for units with time in the denominator).
3. Express the asking rate (look for phrases such as "how fast", "at what rate", "find the rate", etc.).
4. Write an equation that relates the various quantities of the problem.
5. Differentiate both sides of the equation, with respect to time, using the Chain Rule.
6. Substitute the given information into the differential equation and solve for the asking rate.
Note: Problem Solving Strategy
1. If possible, draw a diagram to help visualize the problem.
2. Express the given rates (look for units with time in the denominator).
3. Express the asking rate (look for phrases such as "how fast", "at what rate", "find the rate", etc.).
4. Write an equation that relates the various quantities of the problem.
5. Differentiate both sides of the equation, with respect to time, using the Chain Rule.
6. Substitute the given information into the differential equation and solve for the asking rate.
remaining today
remaining today



