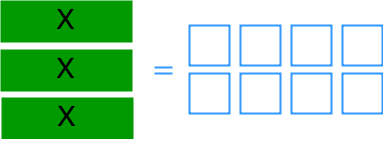
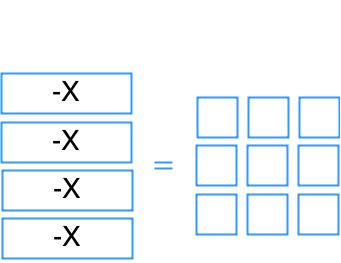
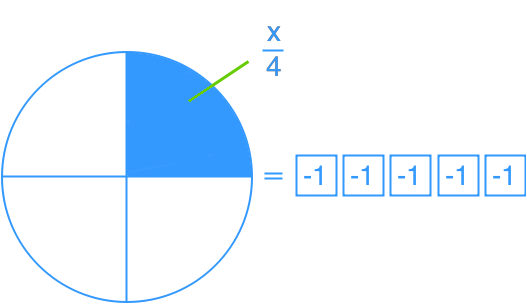Model and solve one-step linear equations: ax = b, x/a = b
All You Need in One PlaceEverything you need for Year 6 maths and science through to Year 13 and beyond. | Learn with ConfidenceWe’ve mastered the national curriculum to help you secure merit and excellence marks. | Unlimited HelpThe best tips, tricks, walkthroughs, and practice questions available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/5
Intros
0/10
Examples
0%