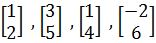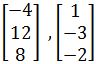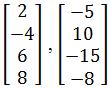Linear independence
All You Need in One PlaceEverything you need for Year 6 maths and science through to Year 13 and beyond. | Learn with ConfidenceWe’ve mastered the national curriculum to help you secure merit and excellence marks. | Unlimited HelpThe best tips, tricks, walkthroughs, and practice questions available. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Lessons
- Linear Independence Overview:
- Linearly independent
• Definition of linear independence
• Trivial solution - Linearly dependent
• Definition of linear dependence
• Non-trivial solutions - Fast ways to determine linear dependence
• Vectors are multiples of one another
• # of Vectors > # of Entries in each vector
• Zero Matrix
Examples
Lessons
- Determining Linear independence by solving
Determine if the following vectors are linearly independent:
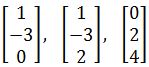
- Determine if the matrix is linearly independent by solving Ax=0:
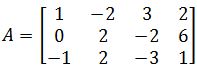
- Determining Linear dependence by inspection
Determine by inspection if the following vectors are linearly dependent: - Linear dependence/independence with unknown constant
Find the value(s) of k for which the vectors are linearly dependent.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Linear Independence
When working with a collection of vectors it is important to know how they are related to each other. There are two possibilities, a set of vectors can either be linearly dependent or linearly independent, and such characteristics can in turn let us know if we are working on a plane, or a subspace, therefore, it is time for us to study these definitions.
A set of vectors 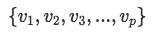 is said to be linearly independent if:
is said to be linearly independent if:
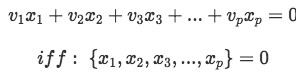
So, the vector set is only linearly independent when the components 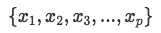 are equal to zero.
are equal to zero.
The reason behind this is that if one of the x terms is not zero, it means you can rewrite the equation solving for one of the vectors, thus, resulting in a vector being able to be written in terms of the others. This is what we call linear dependence of vectors, which means that in a set of vectors you can rewrite one as linear combinations of the others.
Therefore, linearly independent vectors are just as their name implies, they do not depend on any of the other vectors in the set, and so they cannot be written as a linear combination of the others. This can be observed clearer in the next section where we demonstrate the same condition in the form of matrices, for that, make sure you have studied the notation of matrices and representing a linear system as a matrix lessons that are found earlier on this chapter in StudyPug. If you have studied these lessons already but you think you may need a review, we recommend you to go back and check them up again so you can have the topic fresh on your mind before going into the next section of this lesson.
Test for linear independence
Before looking into the methodology to find out if our set is composed of basis vectors being linearly independent we need to make a quick review on how to solve multiplication of matrices:
Please keep in mind equation 2 for problems not only on this lesson but further through this chapter.
Now let us focus on checking for linear independence. If we have the set of vectors:
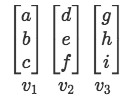
We have that the condition for linear independence of this set goes as follows:
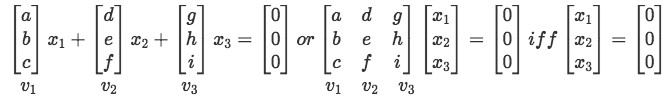
Notice that this is the same a the process represented in equation 1. And in order for us to solve for the components  we use an augmented matrix and the three types of matrix row operations (also known simply as row-reduction) until we find pivots:
we use an augmented matrix and the three types of matrix row operations (also known simply as row-reduction) until we find pivots:

This is what we call the linear independence test. If you would like to see a different approach to the way on testing for linear dependence of vectors, you can take a look at the link embedded for extra review before completing the next examples.
Examples of Linear Independence
Example 1
Determine if the vectors below are linearly independent:
-
We can think of this as a linear combination of vectors in order to test for dependence:
-
In equation for example 1(a) we have rewritten the set of vectors in matrix form following the method used in equation 4 so we can test for linear independence. Remember the set can only be independent if the result is a trivial solution, therefore, if the vectors turn out to be independent, a matrix with pivot points equal to 1 will result in the next operation. Notice how we use an augmented matrix and row-reduction to continue for our solution just as shown in equation 5:
As you notice, all of the components go to zero producing a trivial solution, therefore these vectors are linearly independent.
Example 2
Determine if A is a linearly independent matrix by solving the condition Ax=0.
-
Which is the same as having the set of vectors:
-
Notice this method is exactly the same as the one used in the first problem, the difference is that we started out with the matrix, instead of the separated vectors. Equation for example 1(a) represents the same step as this next formula for this problem:
-
Now we continue solving by row-reducing the augmented matrix until we find the unit pivots.
As you can see, we have obtained a nontrivial solution, which means that the set of vectors given initially cannot be linearly independent (thus, A is a linearly dependent matrix).
For our next four examples we will use a simple method of inspection to tell if two or more vectors are linearly dependent. In simple terms, if a set of vectors has one or more of the next three characteristics in the list below, then is a set of linearly dependent vectors.
- The vectors are multiples of one another
- There are more vectors than there are entries in each vector.
- There is a zero vector
Knowing this, let us work through the next examples, where we will finish off with an interesting and longer problem which will require of a little more robust calculations. For the moment, we concentrate on the inspection method in order to memorize the 3 characteristics above which will be useful in later lessons.
Example 3
By inspection, are the following vectors linearly independent?
-
Condition 1: For this problem, we can easily see the vectors are not multiples of one another. For that, just take a look into the first and second vector, where the first component of the second vector is 3 times the first component of the first vector. When looking at this comparison for the second components of both vectors, we see that we do not have the 1 to 3 relationship, since 2 is not a third of 5. And so, this set of vectors does not agree with the first condition for linear dependency.
-
Condition 2: On this set of 4 vectors we have that each vector contains 2 entries. And thus:
# Vectors > # Entries
Which means this set of vectors is linearly dependent!
-
Condition 3: Just for the sake of checking if the third condition also applies, we revise the set and rapidly notice there is not a zero vector among those in the set, and so, the third condition is not met.
Since the second condition for linear dependence is met, the set of these four vectors is linearly dependent.
Example 4
By inspection, are the following vectors linearly independent?
-
Condition 1: For this case, one might easily conclude these are not vectors which are multiple of each other, they look too different from one another that one might jump into that conclusion, but if we inspect carefully we might find that these are in fact multiples. Let us start with the relationship between the first component of each vector: these components are -4 and 1, if we set this relationship as:
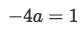
Equation for example 4: Relationship between the first two components of the vectors -
Where a is a proportionality ratio that we need to solve for in order to see if it applies to the rest of the components in the vectors. Thus, we solve for a:

Equation for example 4(a): Proportionality ratio -
So a is the proportionality ratio between the first component on each vector. In other words, if we multiply the first component of the first vector times a, we obtain as a result the first component of the second vector. Let us see now if this works with the rest of the components:
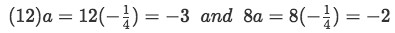
Equation for example 4(b): Applying the proportionality ratio Notice how if we apply the proportionality ratio to the last two components of the first vector, we obtain the last two components of the second vector. And thus, these vectors are multiple of one another and so they are linearly dependent.
Although we already know the solution to this problem, let us still check the other conditions. -
Condition 2: On this set of 2 vectors we have that each vector contains 3 entries. And thus:
# Vectors < # Entries
Which means condition two for linear dependency doesn't apply to this example.
-
Condition 3: The third condition is also not met since there is no zero vector in the set. Therefore, this set of two vectors is linearly dependent due to the first condition only.
Example 5
By inspection, are the following vectors linearly independent?
-
Example 5 turns out to be very simple to solve since we can observe right away that the third condition for linear dependency is met thanks to the second vector in the set, which is a zero vector. Thus, this set of vectors is linearly dependent.
Example 6
By inspection, are the following vectors linearly independent?
-
Condition 1: We look for a proportionality ratio for the two vectors involved on this set, thus, once again we start with the relationship between the first component of each vector: for this case, these components are 2 and -5:

Equation for example 6: Relationship between the first two components of the vectors -
Solving for a:
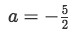
Equation for example 6(a): Proportionality ratio -
Checking if this works with the rest of the components:
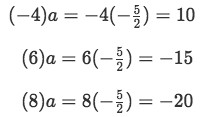
Equation for example 4(b): Applying the proportionality ratio Notice how the first three out of the four components on the second vector, are actually multiples of the first three components on the first vector. Still, the fourth components do not meet the condition for linear dependence, and so, we need to check for the other two conditions to see if one is met.
-
Condition 2: We have 2 vectors with 4 entries each. And thus:
# Vectors < # Entries
Which means condition two for linear dependency doesn't apply to this example.
-
Condition 3: There are no zero vectors among these, and so, the third condition is not met either.
In conclusion, the set of vectors presented in example 6 is linearly independent.
Example 7
Find the values of k for which the vectors are linearly dependent:
-
Since we are working with an unknown constant we cannot directly inspect the set of equations for the conditions of linear dependency, and thus we are left with using the vector equation shown in equations 3 to 5 to produce an augmented matrix that we can row reduce until we can obtain a final solution.
Thus we start by separating the vectors to write them in the equation 4 form, such as:
-
Now we write the equation as an augmented matrix:
-
At this point, we have reduced the third row so that the pivot has been left alone and has a value of k-3. In order to solve for k we need to take into consideration the two possible scenarios that such pivot can produce. One scenario is for k-3=0 or just k=3, the second scenario would then be when k is different to 3 and so we solve for each of these two cases:
-
Case 1: k=3
From this, you can observe that:

Equation for example 7(d): Finding the components of the vector Since x3 is an independent variable, it means it can have any value and thus we set it equal to 1 to obtain: x1=1 and x2=-1, which results in a vector that doesn't correspond to a trivial solution. Thus, for the case in which k=3, the matrix is linearly dependent.
-
Case 2: k ≠ 3
And so we obtain that as long as k is not equal to 3, then the set of vectors are linearly independent.
What does it mean to be linearly independent
To end this lesson and give it a more meaningful notion, let us look into the meaning of linear independence of vectors:
Remember that the second condition on the method of inspection says that if you have a quantity of vectors in a set which is bigger than the number of entries each vector has, then your set contains vectors dependent to each other. This is because we have been looking at sets of column vectors in which each entry represents a component in a different dimension.
Taking equation 3 as out example for vector set once more:
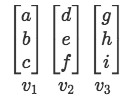
If we rewrite the first vector in the classical notation for a vector in the cartesian coordinate system, you can think of this vector as:
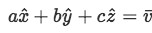
The same can be done to the other two vectors, and once you can think of these 3 vectors as each having components on the 3 dimensions of space (think on the cartesian coordinate system with the 3 axes or dimensions being x, y and z), then it will be very easy to see when they are either linearly dependent or independent of one another and what does this actually represents in physical space.
In other words, if you have a vector with 3 entries, then you have a vector with 3 dimensions, one component in each dimension.If you have a vector with 2 entries, then you have a vector with 2 dimensions or a component in each of two dimensions. And so forth.
Applying the same reasoning to a set of two vectors with two entries, then you have two vectors with two dimensions. And here is where the question arises: Do they linearly depend on each other or are they independent? Physically speaking, these two vectors will be linearly independent of each other if they have different directions. Seen the other way around, the vectors will be linearly dependent if one is the extension of the other, or in other words, if they belong to the same line and have the exact same direction.
And that is where the name of this characteristic comes: "linearly dependent" means it depends on the same line, or is part of the same line, when is not, then it must be a "linearly independent relation". Notice that two independent 2-dimensional vectors define a plane.
For vectors written using the cartesian system, this means that these two vectors have components in x and y, and thus they define the xy-plane. Therefore, if you input any other vector with two entries only, it means it has two dimensions and it will be another vector with components in x and y, belonging to the xy-plane too. Thus the set of these three 2-dimensional vectors would be a linearly dependent set, since the third vector forms part of the same plane as the first two. No matter how many more vectors you input into this set, if they continue to have two entries only, they continue to be part of the same xy-plane and so they are all linearly dependent to each other.
This is the physical meaning of the second condition for the method of inspection, you can have up to the same amount of linearly independent vectors as the amount of entries (dimensions) they have. So if you have 2 entries in each vector, you can have up to 2 independent vectors, if you have 3 entries in each vector, you can have up to 3 independent vectors in the set, if you input any other vector containing the same amount of entries it makes it a linearly dependent set since the extra vector will be defined in the same plane (for two dimensions) or space (for three dimensions) and thus, this extra vector can be represented as a combination of the other ones.
Notice that having 3 vectors with 3 entries does not automatically make a set linearly independent or dependent, it just means you can have up to 3 independent ones. And so for a 3 dimensional set, if you have 3 or 2 vectors, you need to check with other methods shown above if they are independent or not. If more than three 3-dimensional vectors are contained in the set, then you can automatically see the set is linearly dependent.
The meaning of linear independence and dependence can also be seen from the first and third conditions on the inspection method. The first condition is obvious since it says that if the vectors are multiples of each other then they are dependent. Is obvious because by being multiples you are automatically identifying they can be written as combinations of each other. But the third condition of having a zero vector included in the set might not be as direct.
If you have a set of 3 vectors with 3 entries each (3 dimensions) and one of these is a zero vector, then it means that this third vector does not contribute at all to the set (is just a point located at zero, the origin). And so that is how you end up truly with a set of two 3-dimensional vectors and thus, more vectors than dimensions mean they are linearly dependent.
To continue with an explanation on independence, basis and dimensions we recommend you to take a look a the link provided. You can also check out the notes on linear independence found on this last link, where you can see a summarized version of what has been explained on this lesson.
gives only the trivial solution. In other words, the only solution is:
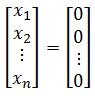
We say that a set of vectors {v1,⋯,vp} in Rn is linearly dependent if:
gives a non-trivial solution. In other words, they are linearly dependent if it has a general solution (aka has free variable).
We can determine if the vectors is linearly independent by combining all the columns in matrix (denoted as A) and solving for
Fast way to tell if 2 or more vector are linearly dependent
1. The vectors are multiples of one another
2. There are more vectors than there are entries in each vector.
3. There is a zero vector
remaining today
remaining today