The characteristic equation
All You Need in One PlaceEverything you need for Year 6 maths and science through to Year 13 and beyond. | Learn with ConfidenceWe’ve mastered the national curriculum to help you secure merit and excellence marks. | Unlimited HelpThe best tips, tricks, walkthroughs, and practice questions available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/4
Intros
Lessons
- The Characteristic Equation Overview:
- What is the Characteristic Equation?
• det(A−λI)=0
• The characteristic polynomial is det(A−λI) - Finding the Eigenvalue
• The eigenvalues of a 2×2 matrix
• The eigenvalues of a 3×3 matrix
• The eigenvalues of a triangular matrix - Shortcut to Determinants of Matrices
• 2×2 matrices
• 3×3 matrices
• Triangular matrices - Eigenvalue with Multiplicity
• Distinct eigenvalues
• Repeated eigenvalues
0/7
Examples
Lessons
- Finding the Characteristic Polynomial
Find the characteristic polynomial of A if:
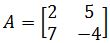
- Find the characteristic polynomial of A if:
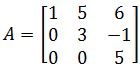
- Finding the Eigenvalues of a 2×2 matrix
Find all the eigenvalues of the matrix
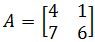
- Finding the Eigenvalues of a 3×3 matrix
Find all the eigenvalues of the matrix
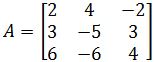
- Finding the Eigenvalues of a triangular matrix
Find all the eigenvalues of the matrix

- Proofs dealing with the Characteristic Equation
Show that A and AT has the same characteristic polynomials. - Suppose A is an n×n triangular matrix where all the diagonal entries are c. Then the characteristic polynomial is
p(λ)=(c−λ)n
Free to Join!
StudyPug is a learning help platform covering maths and science from primary all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
The characteristic equation
The term characteristic equation has various meanings throughout mathematics and its different branches.
For example, there exists a characteristic equation in calculus (also called an auxiliary equation) which is an algebraic expression emulating a homogeneous constant coefficients linear differential equation, and thus having the same order as the differential counterpart, which has as its main purpose to obtain the general solution to the original differential equation. Studypug actually dedicates a few lessons on the calculus characteristic equation depending on the roots needed to solve it, if you are interested in checking these out, the first of a series of three is our lesson on the characteristic equation with real distinct roots.
The same can be said of characteristic equations used to find the general solutions to partial differential equations. To describe the term characteristic equation in simple words, would be to say this is a particular equation containing the main characteristics (elements such as the order) of a larger or more complicated equation (usually from higher level math) in order to help solving the more complicated expression using simpler techniques. In other words, a characteristic equation is used as a trick to solve problems in a more efficient manner.
On this lesson we will focus on what we call the characteristic equation used in linear algebra as a tool while computing the eigenvalues and eigenvectors of a square matrix, so, let us take a look into the details of this next.
Characteristic equation linear algebra
For the characteristic equation linear algebra method, we refer to the characteristic polynomial of a matrix equated to zero as the characteristic equation of a matrix. Such equation is defined as:
From equation 1:
- A represents the given n×n square matrix
- λ is an eigenvalue of A
- I is the n×n identity matrix
- det(A−λI)is the characteristic polynomial
The characteristic polynomial of a 2x2 matrix happens to be equivalent to an algebraic second degree polynomial equation in terms of the variable λ . In other words, for a second order matrix, the characteristic polynomial is a quadratic equation for which we have to solve its roots, and such roots are our eigenvalues λ.
Solving for the eigenvalues of a 2x2 matrix is simple since you only have to use the quadratic formula to calculate the roots. But the task complicates itself as the dimensions of the matrix A increase, for example, the characteristic polynomial of a 3x3 matrix will be a third degree polynomial equation, where you will have to solve for more roots.
In general, the algebraic expression resulting as the characteristic polynomial will be of the same degree as the order of the given matrix A (the dimensions of A), and so, depending on the order of A is the amount of eigenvalues and their corresponding eigenvectors that you will have to calculate.
Knowing that, we can define the term multiplicity for eigenvalues of a matrix, which refers to the repetition (or not) of the found eigenvalues related to a given square matrix A. Simply said, when an eigenvalue is a distinct root of the characteristic polynomial (it is not repeated) then it has a multiplicity of 1; in the other hand, if an eigenvalue is a repeated root of the characteristic polynomial, then it has a multiplicity greater than 1 and will be the defined by the amount of times it is repeated.
Something to know about the characteristic polynomial equation is that similar matrices have the same characteristic polynomial. By definition, two square matrices A and B are similar to each other if they satisfy the next condition:
Similar matrices are matrices which are equivalent to each other in the sense that they share their linear operator and many of their properties such as determinant, trace, rank and since they also share their characteristic polynomial matrix, that means such matrices A and B also have the same eigenvalues. Although we will not dedicate much time to matrix similarity on this lesson, we wanted to introduce it because is the basis for matrix diagonalization, which is the topic of our next lesson in this course. In simple words, a matrix will be diagonalizable if there is a diagonal matrix D which is similar to A.
How to find the characteristic polynomial
In order to calculate an eigenvalue and its corresponding eigenvector for a given matrix A, we have to first find the characteristic polynomial of the matrix; so, in this section we will learn how to find the characteristic polynomial for the two most common cases: a 2x2 matrix and a 3x3 matrix.
We usually focus on matrices of these sizes because the calculations for the determinants of greater order matrices get extensive and are usually not asked for in assignments or general school lessons, but if you find yourself in front of a higher order square matrix for which you have to find its characteristic polynomial (and thus its eigenvalues and eigenvectors), check if this big matrix is a triangular matrix!
Remember there is a trick to find the determinant of a triangular matrix that says you can just multiply the elements on its diagonal and find it. Given that calculations for matrix determinants bigger than a 3x3 get very long, triangular matrices will be a common case to find if the dimensions of the matrix are high. Now, let us look at the steps for the computation of the characteristic polynomial in the two most common cases:
- How to find the characteristic polynomial of a 2x2 matrix
1. First we compute the subtraction of matrices A−λI. The result is a 2x2 matrix.
2. We calculate the determinant of this resulting matrix.
a. Remember the determinant of a 2x2 matrix is calculated with the formula:
3. The result is a quadratic equation (as mentioned before) in terms of λ.
- How to find the characteristic polynomial of a 3x3 matrix
1. First we compute the subtraction of matrices A−λI. The result is a 3x3 matrix.
2. We calculate the determinant of this resulting matrix.
a. Remember the determinant of a 3x3 matrix can be calculated in two ways, the general method and the shortcut method.
b. We recommend you to use the shortcut method to calculate this determinant.
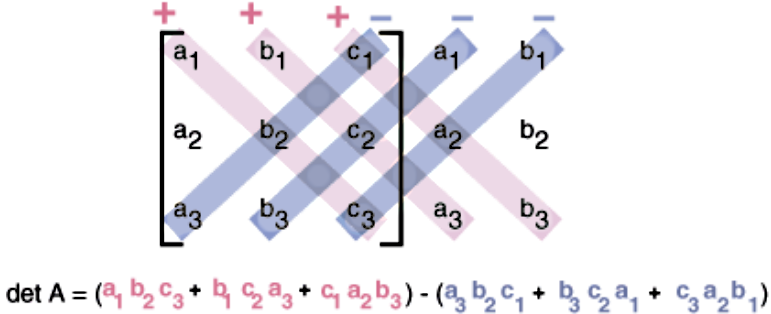
3. The result is a third degree polynomial equation (as mentioned before) in terms of λ.
And now that you have the characteristic polynomial of the matrix provided, you can calculate its eigenvalues and eigenvectors. The complete process for this can be found in our last lesson of that same name.
Finding the characteristic polynomial, example problems
Example 1
Find the characteristic polynomial of A if: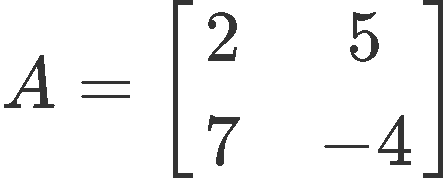
We start by computing the matrix subtraction inside the determinant of the characteristic polynomial, as follows:
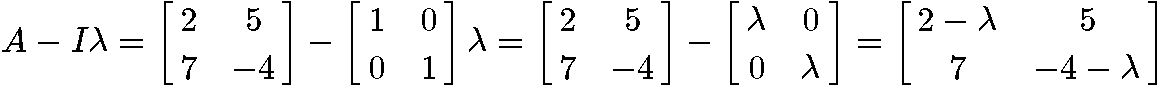
Now using the characteristic equation (equation 1) we solve the determinant of the matrix that resulted from our last step:
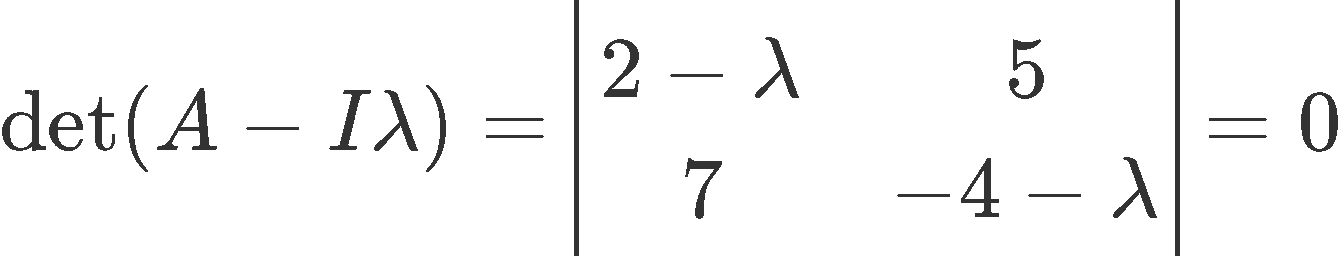
Solving the determinant we have that:
And so, the characteristic polynomial of the 2x2 matrix given on this exercise is: λ2+2λ−43
Remember that if you were asked to calculate the eigenvalues for this matrix, you would just have to use the quadratic equation to find the values of λ .
Example 2
Find the characteristic polynomial of A if:
Starting up with the matrix subtraction A−λI:
Now setting up the determinant in order to calculate the characteristic polynomial expression:
Notice that the square matrix to which we are obtaining its determinant is a triangular matrix, therefore, we can solve its determinant by simply multiplying the elements from its main diagonal. And so, we solve for the final characteristic polynomial equation as follows:
On this occasion, the characteristic polynomial is the third degree polynomial equation: −λ3+9λ2−23λ+15
Example 3
Find all the characteristic equation eigenvalues of matrix A as is defined below:
State the eigenvalues multiplicities, and what type of eigenvalues they are:
From our lesson in eigenvalues and eigenvectors, let us recall the steps to calculate the eigenvalues of a matrix:
- Perform the matrix subtraction A−λI to obtain a new n×n matrix the same size as A.
- Calculate its determinant using the characteristic equation. This determinant is the characteristic polynomial which is a quadratic equation for the case in which A is a 2x2 matrix.
- Use the quadratic formula to solve for λ from the quadratic equation.
Thus we start following the steps and calculate the matrix subtraction:
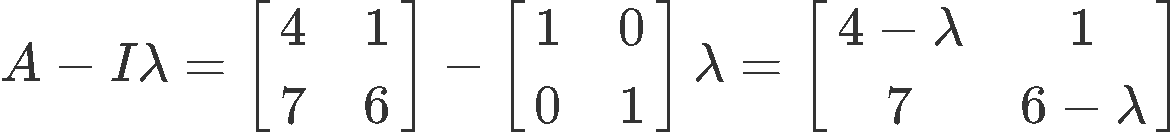
Now we calculate the determinant of the resulting matrix, which is the characteristic polynomial of matrix A:
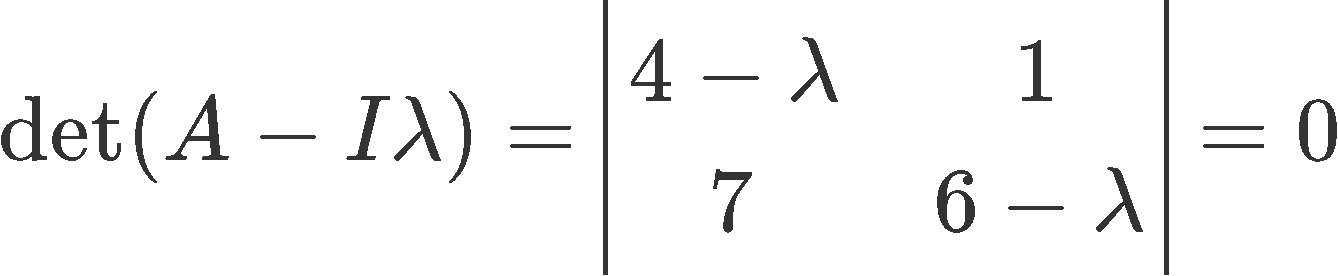
Calculating the determinant:
And so, our characteristic polynomial is:
Now using the quadratic formula to solve for λ:
And so, the eigenvalues are:
Their multiplicity is 1 because they are distinct roots, therefore, they are distinct eigenvalues.
Example 4
Find all the characteristic polynomial eigenvalues for matrix A: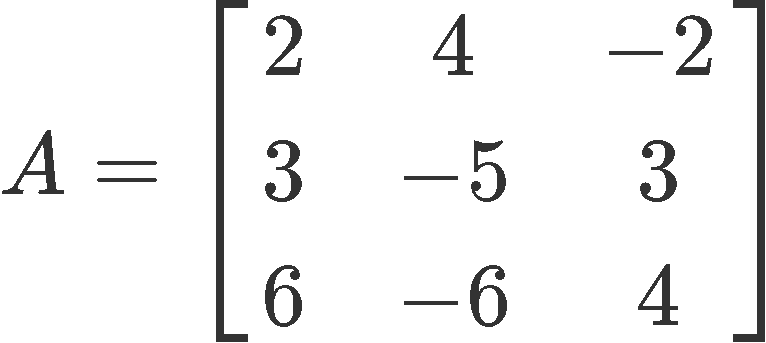
State their multiplicities and what type of eigenvalues they are:
Solving the matrix subtraction A−λI as shown below:
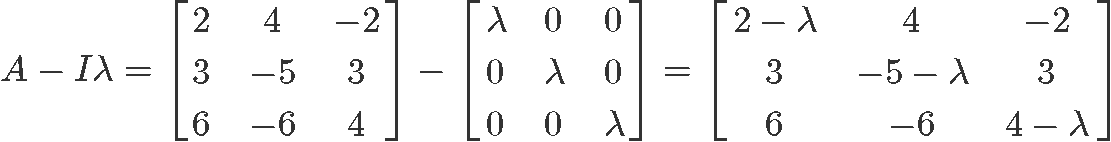
Now we solve the characteristic equation of a 3x3 matrix by obtaining the determinant as follows:
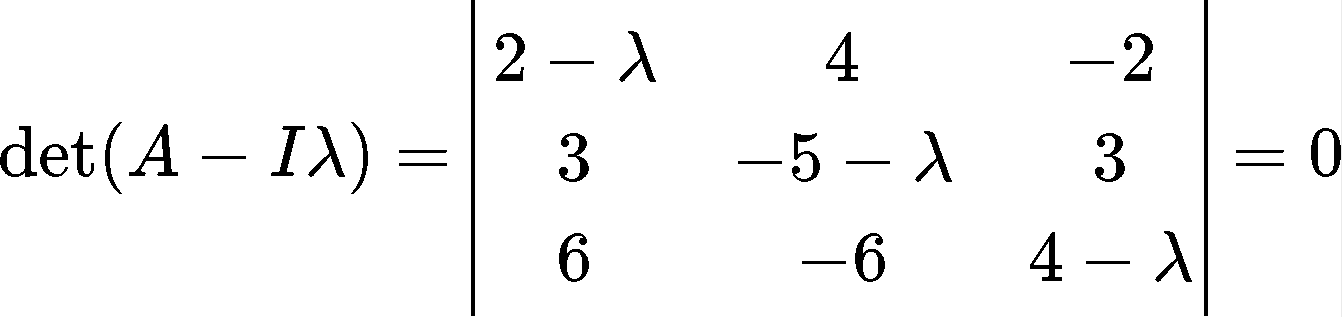
Working through the computation of the determinant in order to obtain the characteristic polynomial:
We stop right here because we will use this last expression: (2−λ)−2+λ+λ2 in a moment when we solve for the eigenvalues. Now lets continue:
The last expression on equation 24 is the characteristic polynomial for this matrix. Now, to solve for the eigenvalues we go back to the last expression we saw in equation 23:
From equation 25 we can automatically see that one of the roots is λ=2, in order to solve the other 2 roots we just solve the quadratic equation for the expression that is left inside the second parenthesis in equation 25.
And so, the eigenvalues are:
Therefore, since all the three eigenvalues λ1=2,λ2=1,λ3=−2 are distinct from each other, their multiplicity is 1, and they are distinct eigenvalues.
Example 5
Find all the eigenvalues of the matrix A as defined below, then, state their multiplicities and what type of eigenvalues they are: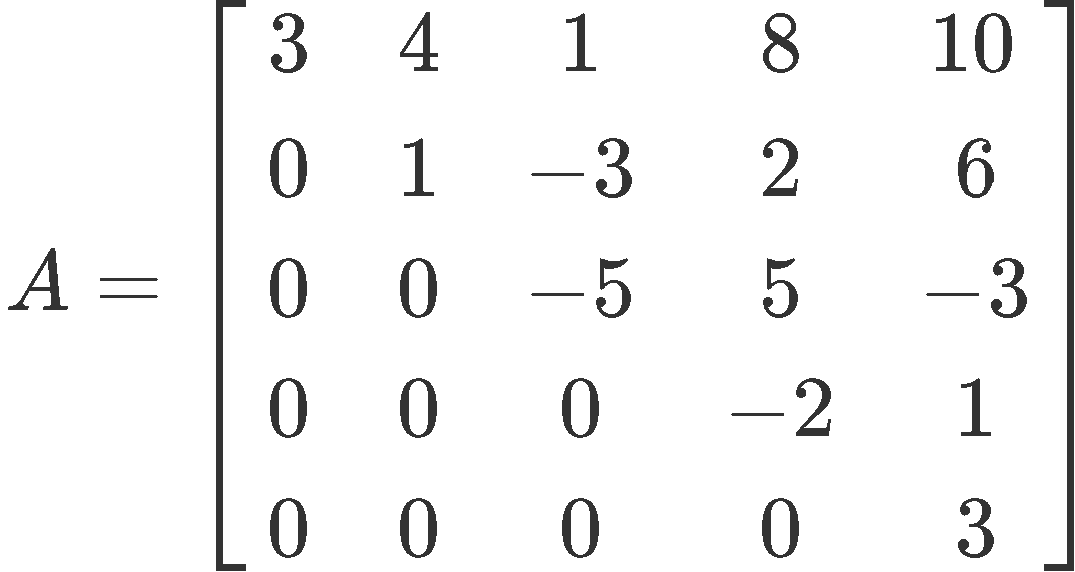
We perform the matrix subtraction A−λI:
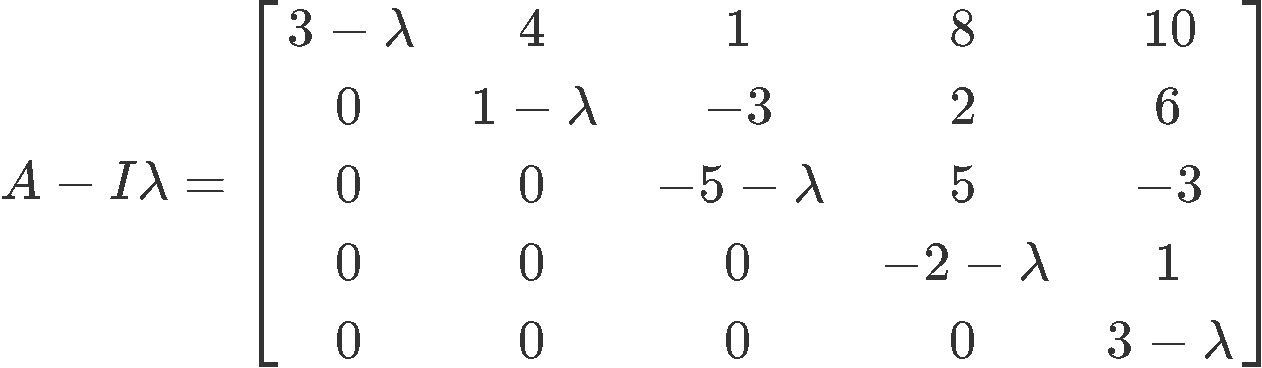
And now we set up the characteristic equation:
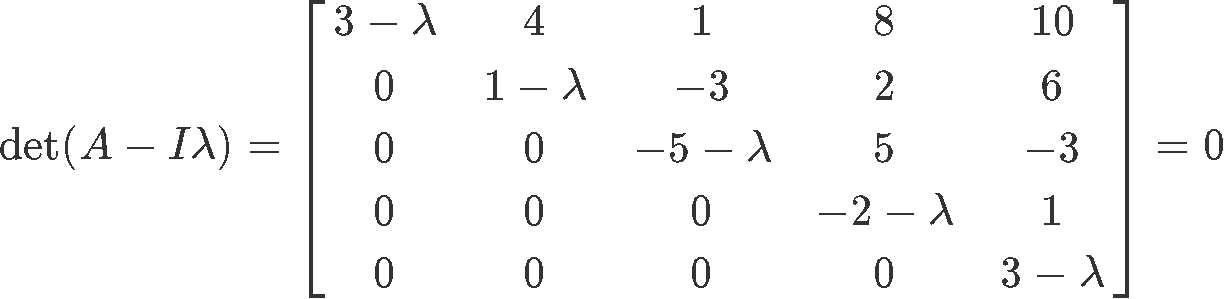
And now, to find the eigenvalues we just compute the determinant shown in equation 30. Notice that since this matrix happens to be a triangular matrix, the only thing to do is to multiply the diagonal components of it to obtain the determinant and so the characteristic polynomial is:
As lucky will have it, there is no need to make anything else on equation 31 in order to obtain the roots for the multiple values of λ. The roots are already given there as factors, and so, the eigenvalues are:
Notice that the eigenvalue equal to 3 repeats itself, therefore =3 is a repeated eigenvalue with multiplicity equal to 2, while the rest of the eigenvalues: λ=1,−5,−2 are all distinct eigenvalues with multiplicity of 1.
To finish off this lesson we recommend you to visit this lesson on eigenvalues and eigenvectors which expands on the importance of the characteristic polynomial equation and its usage while calculating them; we also recommend you to visit this lesson on the characteristic equation which makes sure to define a theorem on algebraic multiplicity and related it with example problems.
This is it for our lesson of today, see you in the next one!
We say that a scalar λ is an eigenvalue of an n×n matrix A if and only if λ satisfies the following characteristic equation:
det(A−λI)=0
We say that det(A−λI) is a characteristic polynomial.
Useful ways to find eigenvalues
When dealing with a 2×2 matrix, use the formula det(A)=ad−bc.
When dealing with a 3×3 matrix, use the shortcut method.
When dealing with a triangular matrix, know that the determinant is just the product of the diagonal entries.
Note that:
1. An eigenvalue is a distinct root if it has a multiplicity of 1
2. An eigenvalue is a repeated root if it has a multiplicity greater than 1
We say that det(A−λI) is a characteristic polynomial.
Useful ways to find eigenvalues
When dealing with a 2×2 matrix, use the formula det(A)=ad−bc.
When dealing with a 3×3 matrix, use the shortcut method.
When dealing with a triangular matrix, know that the determinant is just the product of the diagonal entries.
Note that:
1. An eigenvalue is a distinct root if it has a multiplicity of 1
2. An eigenvalue is a repeated root if it has a multiplicity greater than 1
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



