What are decimals?
Topic Notes
In this lesson, we will learn:
- How to understand decimals using number lines
- How to understand decimals using place values
- How to represent decimals using standard form, expanded form, and written forms
- How to use base ten (block) models to represent decimals
Notes:
- When we look at a number that has multiple digits, each place value is 10 times MORE than the place on its right, and 10 times LESS than the place on its left.
- For example, when we look at the ones place value, we start counting until 10 which starts the tens place value:
- Then, we group ten 10s to get to the next place value of hundreds:
- Continuing, we can then group ten 100s to get to the thousands place value and ten 1000s to get to the ten-thousands place value…etc.
- The same rule applies for decimals! Decimals are place values that are even smaller than the ones place (to the right of the decimal point), and the numbers (place values) are further split into ten parts (divisions).
- This can be shown on a number line, splitting into tenths:



- If we split the number line even further, each tenth can be divided into hundredths and thousandths:


- Standard form shows all the numbers written from left to right, with a decimal point after the ones place
- Ex. 165.407
- Expanded form shows the value of the digit multiplied by how much each place value represents.
- Ex. (1×100) + (6×10) + (5×1) + (4×0.1) +
(0×0.01)+ (7×0.001) - Place values that hold a zero can be left out of expanded form
- Written form shows how to write out decimals as words! Name the number of each digit followed by the name of the place value:
- Ex. one hundred sixty-five and four tenths,
zero hundredths, and seven thousandths
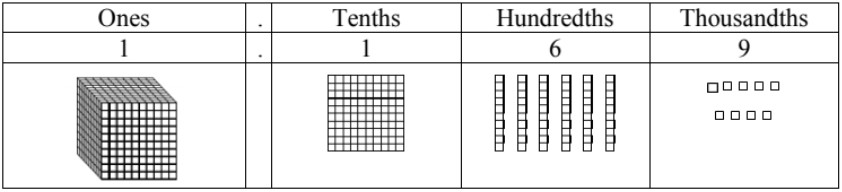
- Our whole numbers will always refer to the ones place value (or greater)
- If our number only represents until the hundredths place, then one whole is one-hundred block:

Introduction: What are Decimals?
Decimals are a fundamental concept in mathematics, representing numbers with fractional parts. They play a crucial role in everyday calculations, scientific measurements, and financial transactions. In the introduction video, we'll explore the basics of decimals and their significance. This article delves into the world of decimals, covering their concept, place values in decimals, and various forms of representation. Decimals extend our number system beyond whole numbers, allowing for precise expressions of quantities between integers. Understanding decimals is essential for advanced mathematical operations and real-world applications. We'll examine how decimals relate to fractions and percentages, and how they're used in different fields. By mastering decimals, you'll enhance your mathematical skills and problem-solving abilities. Join us as we unravel the intricacies of decimal numbers, their structure, and their importance in mathematics and everyday life.
Understanding Decimal Place Values
Place values in decimals are a fundamental concept in mathematics that helps us understand the relative value of each digit in a number. Just as whole numbers have place values, decimals also have a systematic way of representing fractional parts of a whole. Let's explore the concept of place values in decimals, starting from the ones place and moving to the right of the decimal point.
To begin, it's essential to understand that the decimal point serves as a crucial marker. It separates the whole number part from the fractional part of a number. The digits to the left of the decimal point represent whole numbers, while those to the right represent fractions of a whole.
Let's start with the ones place, which is immediately to the left of the decimal point. This place value represents whole units, just like in whole numbers. For example, in the number 5.678, the 5 is in the ones place and represents 5 whole units.
Moving to the right of the decimal point, we encounter the tenths place. This is the first decimal place and represents one-tenth of a whole unit. In our example of 5.678, the 6 is in the tenths place and represents 6/10 or 0.6 of a whole unit.
The next place value to the right is the hundredths place. As the name suggests, this represents one-hundredth of a whole unit. In 5.678, the 7 is in the hundredths place and represents 7/100 or 0.07 of a whole unit.
Following the hundredths, we have the thousandths place. This third decimal place represents one-thousandth of a whole unit. In our example, the 8 is in the thousandths place and represents 8/1000 or 0.008 of a whole unit.
To illustrate how each place value represents a fraction of the whole, let's break down our example number 5.678:
5 (ones) = 5
6 (tenths) = 0.6
7 (hundredths) = 0.07
8 (thousandths) = 0.008
When we add these values together (5 + 0.6 + 0.07 + 0.008), we get 5.678.
It's important to note that as we move to the right of the decimal point, each place value represents a smaller fraction of the whole. The tenths are larger than the hundredths, which are larger than the thousandths, and so on.
Comparing decimal place values to whole number place values can help reinforce this concept. In whole numbers, as we move to the left, each place value is ten times greater than the one to its right. For example, in the number 123, the 1 represents 100, the 2 represents 20, and the 3 represents 3.
Similarly, in decimals, as we move to the right of the decimal point, each place value is one-tenth of the one to its left. This pattern continues indefinitely, with each subsequent place value representing a smaller fraction of the whole.
Understanding place values in decimals is crucial for various mathematical operations, including adding decimal values, subtraction, multiplication, and division of decimal numbers. It also plays a vital role in rounding decimals and comparing their relative sizes.
In practical applications, decimal place values are used extensively in measurements, financial calculations, and scientific notation. For instance, when measuring length, we might use meters (whole units), centimeters (hundredths), and millimeters (thousandths). In finance, currency is often expressed using two decimal places to represent cents.
As you work with decimals, remember that each digit's position relative to the decimal point determines its value. This understanding will help you manipulate and interpret decimal numbers accurately in various mathematical and real-world contexts.
Decimal Representation on a Number Line
Representing decimals on a number line is a fundamental concept in mathematics that helps visualize the relationship between whole numbers and their fractional parts. A number line is a powerful tool for understanding how decimals fit into the numerical system, allowing us to see their relative positions and values clearly.
To begin, let's consider a basic number line with whole numbers. Between any two consecutive whole numbers, there exists an infinite number of decimal values. To represent these decimals, we need to divide the space between whole numbers into smaller, equal parts.
The process of representing decimals starts by dividing the space between whole numbers into tenths. This means that the distance between any two consecutive whole numbers is split into ten equal parts. Each of these parts represents one-tenth (0.1) of the distance. For example, between 0 and 1, we would have markings for 0.1, 0.2, 0.3, and so on up to 0.9.
To represent hundredths, we further divide each tenth into ten equal parts. This creates a finer division where each small segment represents one-hundredth (0.01) of the distance between whole numbers. For instance, between 0.1 and 0.2, we would have markings for 0.11, 0.12, 0.13, and so forth.
For even more precise representations, we can divide the hundredths into ten equal parts to show thousandths. Each of these tiny divisions represents one-thousandth (0.001) of the distance between whole numbers. This level of detail allows us to pinpoint very small decimal values on the number line.
Let's look at an example of locating a specific decimal on the number line. To place 0.375 on the number line, we would first identify that it falls between 0 and 1. Then, we'd locate the third tenth (0.3), move to the seventh hundredth after that (0.37), and finally to the fifth thousandth (0.375).
The concept of zooming in is crucial when working with decimals on a number line. As we zoom in, we can see finer divisions, allowing us to represent smaller decimal values more accurately. For instance, zooming in on the section between 0.3 and 0.4 would reveal the hundredths, making it easier to place numbers like 0.35 or 0.38.
This zooming process can be continued indefinitely, theoretically allowing us to represent any decimal number, no matter how many decimal places it has. It's important to note that as we zoom in, the scale of the number line changes, but the relative positions of the numbers remain the same.
Understanding how decimals are represented on a number line is essential for grasping concepts like ordering decimals, comparing their values, and performing operations with them. It provides a visual aid that helps in comprehending the dense nature of decimal numbers and their relationship to whole numbers and fractions.
In practical applications, such as measurements or scientific calculations, the ability to visualize decimals on a number line becomes invaluable. It allows for precise positioning and helps in estimating values between marked points. This skill is particularly useful in fields like engineering, physics, and finance, where accurate decimal representations are crucial.
By mastering the representation of decimals on a number line, students and professionals alike can develop a stronger intuition for numerical values and improve their overall mathematical reasoning. This foundational skill paves the way for more advanced mathematical concepts and real-world problem-solving abilities.
Forms of Writing Decimals
Understanding the different forms of writing decimals is crucial for mastering mathematical concepts and real-world applications. Decimals can be represented in three primary forms: standard form, expanded form, and written form. Each of these forms provides a unique way to express decimal numbers, emphasizing different aspects of their structure and value.
Standard form is the most common way of writing decimals. In this form, digits are arranged in order from left to right, with a decimal point separating the whole number part from the fractional part. For example, 3.14 is a decimal in standard form. The digits to the left of the decimal point represent whole numbers, while those to the right represent fractions of one. Understanding place values is essential when interpreting decimals in standard form. Each digit's position relative to the decimal point determines its value.
Expanded form breaks down a decimal into the sum of its individual place values. This form clearly shows the value of each digit based on its position. For instance, 3.14 in expanded form would be written as 3 + 0.1 + 0.04. This representation helps in visualizing the composition of the decimal number. To convert from standard form to expanded form, identify the place value of each digit and express it as a sum. For example, 45.678 in expanded form would be 40 + 5 + 0.6 + 0.07 + 0.008.
Written form expresses decimals using words rather than numerals. This form is particularly useful in contexts where clarity is paramount, such as in legal documents or when writing checks. For example, 3.14 in written form would be "three and fourteen hundredths." When writing decimals in this form, it's important to use the correct place value terminology. The whole number part is written as usual, followed by the word "and," and then the fractional part is expressed as a fraction over its place value.
Converting between these forms requires a solid understanding of place values. When moving from standard form to expanded form, each digit is multiplied by its corresponding place value. For instance, in 23.45, the 2 represents 20, the 3 represents 3, the 4 represents 0.4, and the 5 represents 0.05. To convert from expanded form to standard form, simply add up the individual components and align the decimal point accordingly.
The importance of understanding place values cannot be overstated when working with decimals. Each digit's position relative to the decimal point determines its value, with each place to the right of the decimal point representing a power of 1/10. For example, in 0.123, the 1 is in the tenths place (1/10), the 2 is in the hundredths place (1/100), and the 3 is in the thousandths place (1/1000).
Mastering these different forms of decimal representation enhances mathematical fluency and problem-solving skills. Standard form is efficient for calculations and everyday use. Expanded form aids in understanding the composition of decimal numbers and is particularly useful in teaching and learning contexts. Written form ensures clear communication of decimal values in non-technical settings.
Practice converting between these forms to reinforce your understanding of decimals and place values. Start with simple decimals and gradually increase complexity. Remember that regardless of the form used, the value of the decimal remains the same. This versatility in representation allows for flexibility in mathematical communication and problem-solving approaches.
Base-10 Models for Decimals
Base-10 models are powerful tools for representing and understanding decimal numbers. These visual aids help students grasp the concept of place value and the relationship between whole numbers and fractions. By using different blocks to represent ones, tenths, hundredths, and thousandths, base-10 models provide a tangible way to explore decimal representation.
In a base-10 model for decimals, each block represents a specific place value. The largest block typically represents one whole unit. This "ones" block serves as the foundation for understanding smaller decimal parts. It's crucial to identify and recognize this whole unit as it forms the basis for all other decimal representations.
Moving to the right of the ones block, we encounter smaller blocks representing tenths. In a physical model, these are often depicted as flat squares that are one-tenth the size of the ones block. Ten of these tenth blocks would be equivalent to one whole unit. This visual representation helps students understand that 0.1 is one-tenth of 1, and that it takes ten of these parts to make a whole.
Continuing further, we find even smaller blocks representing hundredths. These are typically shown as thin rods or long rectangles, each being one-hundredth the size of the ones block. It takes 100 of these hundredth blocks to equal one whole unit. This visual aids in comprehending that 0.01 is one-hundredth of 1, and that 10 hundredths make up one tenth.
The smallest blocks in most base-10 decimal models represent thousandths. These are often depicted as tiny cubes, each being one-thousandth the size of the ones block. It requires 1,000 of these minuscule blocks to equal one whole unit. This representation helps students visualize that 0.001 is one-thousandth of 1, and that 10 thousandths constitute one hundredth.
Using these models, students can easily visualize and understand decimal values. For example, to represent 1.234, one would use one "ones" block, two "tenths" blocks, three "hundredths" blocks, and four "thousandths" blocks. This physical or visual arrangement clearly shows the composition of the number and how each digit relates to the whole.
Base-10 models are particularly useful for comparing decimal numbers. By placing two different decimal representations side by side, students can visually determine which is greater. For instance, comparing decimal numbers like 0.5 and 0.25 becomes intuitive when students see that five tenth blocks take up more space than two tenth blocks and five hundredth blocks.
These models also excel at demonstrating equivalent representations. Students can physically or mentally manipulate the blocks to show that 0.5 is the same as 0.50 or 0.500. This hands-on approach reinforces the concept that adding zeros after the last non-zero digit in a decimal doesn't change its value.
Moreover, base-10 models facilitate understanding of decimal addition and subtraction. Students can combine or remove blocks to perform these operations visually. For example, adding 0.3 and 0.12 can be done by combining three tenth blocks with one tenth block and two hundredth blocks, resulting in 0.42.
The importance of identifying the 'whole' in these models cannot be overstated. It serves as a reference point for all decimal parts and helps students maintain perspective on the relative sizes of decimal fractions. Understanding that all the smaller parts relate back to this whole unit is fundamental in grasping the concept of decimals.
As students become more comfortable with base-10 models, they develop a stronger intuition for decimal place value. This foundation is crucial for more advanced mathematical concepts, including decimal multiplication, division, and conversion between fractions and decimals.
In conclusion, base-10 models offer a concrete, visual method for representing decimals. By utilizing blocks to represent ones, tenths, hundredths, and thousandths, these models provide a tangible way to understand and manipulate decimal values. The ability to visualize these relationships strengthens students' overall comprehension of the decimal system, setting a solid foundation for future mathematical learning.
Practical Applications of Decimals
Decimals play a crucial role in our everyday lives and various professional fields, making them an essential concept to understand for practical problem-solving. These real-world applications of decimals are far-reaching and impact numerous aspects of our daily routines and specialized industries.
One of the most common uses of decimals is in measurements. Whether we're cooking, constructing, or conducting scientific experiments, precise measurements often involve decimal notation. For instance, when following a recipe, we might need to measure 0.5 cups of sugar or 2.25 teaspoons of vanilla extract. In construction, architects and engineers rely on decimal measurements to ensure structural integrity, using dimensions like 10.75 inches or 3.2 meters.
Money is another area where decimals are ubiquitous. Our financial systems are built on decimal currency, with dollars and cents represented as decimal values. When shopping, we encounter prices like $19.99 or calculate discounts such as 15% off. In personal finance, understanding decimals is crucial for budgeting, calculating interest rates on loans or savings accounts, and managing investments.
Scientific notation, which uses decimals, is indispensable in fields like astronomy, physics, and chemistry. It allows scientists to express very large or very small numbers efficiently. For example, the speed of light can be written as 3.0 × 10^8 meters per second, and the mass of an electron as 9.1 × 10^-31 kilograms. This notation enables researchers to work with extreme values and perform complex calculations with ease.
In the medical field, decimals are vital for accurate dosing of medications. Pharmacists and healthcare professionals must precisely measure and administer drugs, often in milligrams or milliliters, using decimal notation. A slight error in decimal placement could have serious consequences, highlighting the importance of decimal proficiency in healthcare.
The use of decimals extends to many other professions and daily activities. Meteorologists use decimals to report temperature, rainfall, and wind speed. Athletes and fitness enthusiasts track their performance using decimal measurements for time, distance, and weight. In retail, pricing strategies often involve decimal points to create psychological pricing effects.
Understanding decimals is also crucial in data analysis and statistics. Percentages, which are essentially decimals multiplied by 100, are used to represent everything from election results to market share. In business, decimals are used in financial reports, inventory management, and performance metrics.
As we navigate an increasingly data-driven world, the ability to interpret and work with decimals becomes even more critical. From understanding the nutritional information on food labels to analyzing energy consumption in our homes, decimals are integral to informed decision-making and problem-solving in our daily lives.
In conclusion, the real-world applications of decimals are vast and varied, touching nearly every aspect of our personal and professional lives. From precise measurements and financial calculations to scientific notation and data analysis, decimals provide the foundation for accurate quantification and problem-solving across numerous fields. Mastering decimals is not just an academic exercise but a practical skill that enhances our ability to understand and interact with the world around us.
Conclusion
In this comprehensive guide on decimals, we've explored the fundamental concepts that form the backbone of decimal understanding. We've delved into the crucial role of place values in decimals, emphasizing how each digit's position determines its value. The article has covered various forms of decimal representation, including decimal fractions and mixed numbers, providing a well-rounded view of how decimals can be expressed. Understanding these concepts is essential for mathematical proficiency and real-world applications. To truly master decimals, regular practice is key. We encourage readers to engage with the exercises provided and seek out additional problems to reinforce their skills. For those looking to deepen their knowledge, the introduction video offers a visual explanation of decimal basics. Remember, a solid grasp of decimals is fundamental to more advanced mathematical concepts, making it a worthwhile investment of your time and effort.
By understanding place values in decimals, students can better comprehend the significance of each digit in a number. Additionally, practicing with mixed numbers can enhance their ability to handle more complex mathematical problems. These foundational skills are crucial for success in higher-level math courses and everyday financial literacy.
Introduction to Decimals: What are Decimals and How Do You Read Decimals on a Number Line?
Decimals are a way of representing numbers that are not whole. They are used to express values that fall between whole numbers, allowing for more precise measurements and calculations. Understanding decimals involves knowing place values and how to read them on a number line. This guide will walk you through the basics of decimals and how to interpret them on a number line.
Step 1: Understanding Place Values
To understand decimals, it's essential to first grasp the concept of place values. Place values determine the value of a digit based on its position in a number. For example, in the number 1111, the place values from left to right are thousands, hundreds, tens, and ones. Each place value is ten times greater than the one to its right. This means that:
- The thousands place represents 1000s.
- The hundreds place represents 100s.
- The tens place represents 10s.
- The ones place represents 1s.
When we write numbers, each digit can only be between 0 and 9. Once we reach 10, we move to the next place value. For example, 10 in the ones place becomes 1 in the tens place and 0 in the ones place.
Step 2: Introducing Decimals
Decimals extend the place value system to represent values smaller than one. The decimal point separates the whole number part from the fractional part. For example, in the number 1111.111, the digits to the right of the decimal point represent fractional values:
- The first place after the decimal point is the tenths place (0.1).
- The second place is the hundredths place (0.01).
- The third place is the thousandths place (0.001).
Each place value to the right of the decimal point is ten times smaller than the one to its left. This means that 0.1 is ten times smaller than 1, 0.01 is ten times smaller than 0.1, and so on.
Step 3: Counting with Decimals
Counting with decimals is similar to counting whole numbers, but it involves fractional values. For example, starting from 0, you can count in tenths: 0.1, 0.2, 0.3, and so on, up to 1.0. When you reach 1.0, you have counted ten tenths, which equals one whole number. You can continue counting: 1.1, 1.2, 1.3, and so on.
Similarly, you can count in hundredths: 0.01, 0.02, 0.03, and so on, up to 0.10 (which is the same as 0.1). This process can be extended to thousandths and beyond.
Step 4: Reading Decimals on a Number Line
Decimals can be represented on a number line, which helps visualize their values. A number line typically shows whole numbers, but the spaces between these numbers can be divided into smaller parts to represent decimals. For example, the space between 0 and 1 can be divided into ten equal parts to represent tenths:
- 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0
Each of these points represents a tenth of the distance between 0 and 1. You can further divide these tenths into hundredths by splitting each tenth into ten equal parts:
- 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10
This process can be repeated to represent thousandths and smaller values. By zooming in on the number line, you can see increasingly smaller divisions, allowing for precise placement of decimal values.
Step 5: Practical Application
Understanding decimals and their place values is crucial for various real-world applications, such as measuring lengths, weights, and volumes. For example, when measuring length, you might use a ruler that shows centimeters and millimeters. Each centimeter can be divided into ten millimeters, representing tenths of a centimeter. Similarly, in financial transactions, decimals are used to represent cents, with 100 cents making up one dollar.
By mastering the concept of decimals and how to read them on a number line, you can accurately interpret and work with fractional values in everyday situations.
FAQs
-
What is the difference between a decimal and a fraction?
Decimals and fractions are both ways to represent parts of a whole, but they use different notations. Decimals use a decimal point to separate whole numbers from fractional parts and are based on powers of 10. For example, 0.5 is a decimal. Fractions use a numerator and denominator separated by a line, like 1/2. While they represent the same value, decimals are often easier to use in calculations and are more common in everyday contexts like money and measurements.
-
How do you convert a decimal to a percentage?
To convert a decimal to a percentage, multiply the decimal by 100 and add the % symbol. For example, to convert 0.75 to a percentage:
0.75 × 100 = 75%
Conversely, to convert a percentage to a decimal, divide by 100 or move the decimal point two places to the left. For instance, 25% as a decimal is 0.25.
-
What is the importance of place value in decimals?
Place value is crucial in decimals as it determines the value of each digit based on its position relative to the decimal point. Each place to the right of the decimal point represents a power of 1/10. For example, in 0.234:
- 2 is in the tenths place (2/10 or 0.2)
- 3 is in the hundredths place (3/100 or 0.03)
- 4 is in the thousandths place (4/1000 or 0.004)
Understanding place value is essential for reading, writing, and performing operations with decimals accurately.
-
How do you round decimals?
To round decimals, look at the digit immediately to the right of the desired rounding place. If this digit is 5 or greater, round up; if it's less than 5, round down. For example, to round 3.14159 to two decimal places:
- Look at the third decimal place (1).
- Since 1 is less than 5, we round down.
- The result is 3.14.
Rounding is useful for simplifying numbers and estimating calculations.
-
What are some common real-world applications of decimals?
Decimals are widely used in everyday life and various professions:
- Finance: Money calculations, interest rates, and financial reports
- Measurements: Cooking recipes, construction, and scientific experiments
- Sports: Recording times, distances, and statistics
- Technology: Computer programming and digital storage sizes
- Science: Precise scientific notation and data analysis
Understanding decimals is crucial for interpreting and working with numerical information in these and many other areas.
Prerequisite Topics
Understanding decimals is a crucial concept in mathematics, but to fully grasp this topic, it's essential to have a solid foundation in certain prerequisite areas. Two key concepts that are fundamental to understanding decimals are place value and basic arithmetic operations, particularly addition and subtraction.
Let's start with place value. This concept is the cornerstone of our number system and is especially important when working with decimals. In the decimal system, each digit's position determines its value. When we move to the right of the decimal point, we enter the realm of fractional parts, where understanding place value becomes even more critical. For instance, the concept of the thousandths place value is essential for reading and writing decimals accurately.
Consider a number like 3.456. The digit 3 is in the ones place, 4 is in the tenths place, 5 is in the hundredths place, and 6 is in the thousandths place. Without a solid grasp of place value, it would be challenging to understand what these numbers truly represent and how they relate to whole numbers and fractions.
Moving on to arithmetic operations, addition and subtraction form the basis for working with decimals. While these operations might seem straightforward with whole numbers, they require extra care and understanding when applied to decimals. The ability to perform decimal addition and subtraction accurately is crucial for more advanced mathematical concepts and real-world applications.
For example, when adding or subtracting decimals, it's essential to align the decimal points correctly. This alignment is directly related to understanding place value. Without this foundation, students might struggle with tasks like balancing a checkbook or calculating discounts, where precise decimal calculations are necessary.
Furthermore, these prerequisite skills pave the way for more complex operations with decimals, such as multiplication and division. They also form the groundwork for understanding percentages, ratios, and even algebraic concepts involving decimal coefficients.
In conclusion, mastering place value and basic addition and subtraction operations is not just about ticking off items on a curriculum checklist. These skills are fundamental building blocks that enable students to work confidently with decimals, preparing them for more advanced mathematical concepts and real-world problem-solving. By ensuring a strong foundation in these prerequisite topics, students can approach the study of decimals with greater understanding and success.

