Characteristic equation with repeated roots
All You Need in One PlaceEverything you need for Year 6 maths and science through to Year 13 and beyond. | Learn with ConfidenceWe’ve mastered the national curriculum to help you secure merit and excellence marks. | Unlimited HelpThe best tips, tricks, walkthroughs, and practice questions available. |
Make math click 🤔 and get better grades! 💯Join for Free
Intros
Examples
Lessons
- Determining the Characteristic Equation with Repeated Roots
Find the particular solution to the following differential equation:
y′′−6y′+9y=0
With initial values y(0)=3,y′(0)=2 - Find the particular solution to the following differential equation:
4y′′−12y′+9y=0
With initial values y(2)=e3,y′(2)=21e3
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Characteristic equation with repeated roots
The characteristic equation
Reviewing what we saw in the past two lessons on real distinct roots and complex roots, remember that the characteristic equation of a differential equation is an algebraic expression which is used to facilitate the solution of the differential equation in question. And so for these three lessons (the two mentioned and this one) where we are looking for the particular solutions of second order constant coefficients linear homogeneous differential equations we can transcribe a second order linear differential equation into a second degree algebraic equation and thus solving for the values of this equation in simpler math.
This auxiliary conversion from differential math to algebra produces an expression we call a characteristic equation. For this particular lesson, we will be looking into second order differential equations which produce repeated roots from their characteristic equation. That means, the discriminant resulting from such characteristic equations is equal to zero.
Having a second order constant coefficients linear homogeneous differential equation of the form:
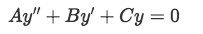
We know that we can rewrite this equation as a characteristic algebraic expression form such as:
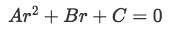
As mentioned before, for the method we are studying today, repeating roots means that when you solve the characteristic equation you will find there is only one possible value of r. If we think of it in terms of the characteristic equation, its constant coefficients and their arrangement in the quadratic formula while solving for r, we find that the term inside the square root vanishes, and thus vanishing the chances of obtaining a set of two values for r.
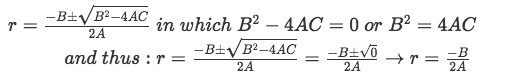
And so, this agrees with the conditions we have talked about in the two past lessons for different types of roots that can be found while solving second order differential equations like the one in equation 1.
| Discriminant | Roots |
|
B2−4AC=positive B^{2} > 4AC |
Real and distinct roots |
|
B2−4AC=negative B^{2} < 4AC |
Complex roots |
|
B2−4AC=0 B2=4AC |
Repeated roots |
Once more, before we continue onto heavier computations, we recommend that if you have not studied the past two lessons or if it has been awhile since you last studied these topics, please go back and check a few lessons before continuing to our next section. Topics we recommend to look out for review are the quadratic function in general form, quadratic equations, the quadratic formula, the discriminant, solving quadratic equations by completing the square, etc so you are prepared for what is coming next.
Double roots
The resultant repeated roots for the characteristic equation where we find the discriminant to be equal to zero, are sometimes called double roots. This name becomes quite obvious when we take a look at the next section in problem example 1, where you will obtain a characteristic equation from the 2nd order differential equation and you can easily obtain the value of the root by factoring this characteristic equation into a notable product called a binomial squared. That means, your quadratic equation which is characteristic of the differential equation you are trying to solve, can be simplified as the multiplication of a binomial by itself, or "seeing the binomial double".
Sometimes this particular approach is not visible as easily as in problem example 1, like in example 2. Therefore, in example 2 we will use the quadratic equation to solve for the repeated root. This doesn't mean the "double root" characteristic does not apply to the equation in example 2, it does! If you do some reverse engineering by computing the square of the binomial r-3/2, you will see that multiplying this binomial by itself you get back a quadratic function which is a multiple of the characteristic equation for that problem.
In conclusion, a repeated root is also called a double root because it solves a quadratic equation that can be factorized including a product that is a binomial squared.
How to solve second order differential equations when they have repeated roots:
By having only one root value coming out of the characteristic equation it would be easy to think that this would facilitate the way we solve these type of problems since intuitively, this would shorten the form of the general solution to the differential equation in relation to the problems where you find real roots or complex roots. In reality this actually complicates a little bit our way since we cannot rely on having only one term in the general solution form to comply with a set of two initial conditions every time, and thus, we need to, look for a way to find the other term in our general solution.
Notice that in this case the single value of r is a real number, and thus, is a real root. Now think back on the method to solve a differential equation with real distinct roots where you have a general solution in the form of:
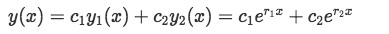
Relating this equation to our topic of today, since you only have one real r, then you could say you only have the part of the general solution corresponding to y1(x) and so, we need to find the term for y2(x)). For that, our best bet is to define this second term as the first term multiplied by a function of x, which we will call v(x). And so we define both terms as:
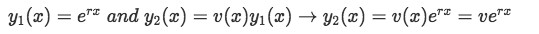
So our general solution for our differential equation with repeated roots would end up being the addition of the y terms shown in equation 5, accompanied by some constant coefficients. If this is true, it means that if we find the expression for v(x) we can completely write the general solution form for a differential equation with repeated roots… Let us find v then!
We start by substituting the known expression for r into the equation for y2(x) (plug r in terms of the constant coefficients as shown in equation 3) and then we obtain the first and second derivatives of it:
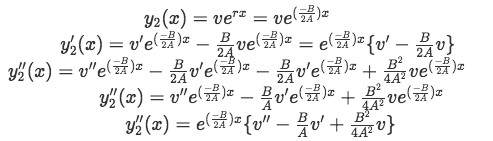
Then we plug all of these into the general form of the second order constant coefficients linear homogeneous differential equation in order to solve for v(x) as follows:
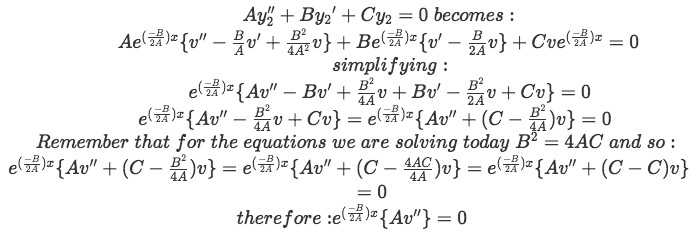
From the result in equation 7 we can conclude that v''=0 for two main reasons: For one, e to any power cannot be zero, even when elevated to the power of 0 you will obtain a 1 as a result, therefore the term containing e cannot be equal to zero. Our second reason is that A cannot be zero either. Take a look at equation 1 and observe that if you make A equal to zero this converts the equation from second order to first order, and therefore is a completely different methodology to find its result; and so, since we are looking for the solution to a second order differential equation here, A cannot be zero. Thus, the second derivative of v(x) is equal to zero.
With all this in mind, what is v(x) then? For that, we can easily obtain the next results:
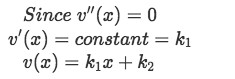
If the second derivative of v is zero, it means that the first derivative is a constant (which we decided to name k1). This result is gotten through a simple integration.
We integrate again to obtain the value of v(x) and notice we have put names to the unknown constants just to keep an eye on them. Remember that whenever you find many constants operating on each other you can combine them into a new one (it doesn't matter since it just means you have a new unknown number), and that is exactly what we will do in our next step to simplify when obtaining the formula for the general solution of a differential equation.
So we come to the important result which is our final expression for the general solution of a second order differential equation with repeated roots. Looking back at equations 4 and 5 we use them to write it in a similar form:
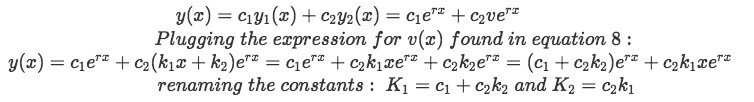
So we finally find our final expression for the solution to second order differential equations with repeated roots:
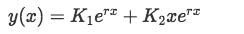
If you notice, this final expression is very similar to that found in the lesson for real distinct roots.
At this point is important to note that you do not have to work through all of the calculations shown after equation 3 and until equation 9. We only worked through these expressions in order to find v(x) and prove it is a good fit to complete our general solution. In truth, the method you need to follow in order to solve a differential equation with repeated roots is simple once you have the complete form of the general solution, it starts with equations 1 through 3, and then jumps until equation 10. As always, we have taken the time to decompose this process into simple steps in the next paragraphs for you to follow. So relax and take equation 10 as your tool to solve these problems in an easy and fast way.
Steps to solve second order constant coefficient linear homogeneous differential equations where you find repeated roots through their characteristic equation:
- Transcribe the equation in the characteristic equation form.
- Obtain the repeated roots value (which by definition is r=−2AB)
- Remember that depending on the characteristic equation found, the root can be found by factorization, by using the quadratic equation or simply by calculating the value from the definition. Use whichever method you prefer, just keep in mind that the very last option (the one using the definition r=−2AB might not be practical since many problems will ask you to solve for a differential equation but will not tell you if it has repeated roots, therefore, this can only be used when you know the equation will contain repeated roots beforehand.
- Plug the values of r into the general form of the differential equation shown in equation 10.
- Obtain the first derivative of the general solution to the differential equation and then apply the initial conditions in order to solve for the two unknown constants.
- Obtain the particular solution to the differential equation by plugging the found values of the unknown constants.
Now let us work through some examples:
Example 1
Find the particular solution to the differential equation below having the initial values of y(0)=3 and y'(0)=2.
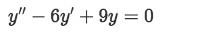
- Step 1:
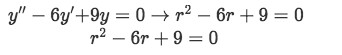
Equation for example 1(a): Characteristic equation -
Step 2:
Notice that our characteristic equation is a notable product, in other words, this is a recognized special binomial product called a binomial squared, therefore is very easy to obtain the value of the repeated roots by factorization:

Equation for example 1(b): Finding the repeated root -
Step 3:
Plugging the value of the repeated root into our equation 10 we find the general solution of the differential equation:
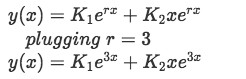
Equation for example 1(c): Finding the general solution to the differential equation -
Step 4:
We compute the first derivative of the general solution and having that, we apply the initial value conditions of y(0)=3 and y'(0)=2 to both, the general solution and its derivative, in order to find the values of the two unknown constants on the equation above:
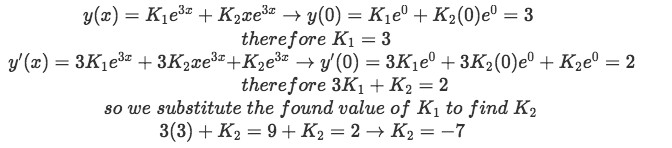
Equation for example 1(d): Finding the values of the unknown constants in the general solution -
Step 5:
We substitute the found values of the unknown constants into the general solution, and our result is the particular solution to the second order constant coefficients linear homogeneous differential equation:
Now let us pass into a second example which contains a little more difficult set of initial conditions. As always, do not get discouraged, just follow the simple steps listed above and you should be able to arrive to the answer easily.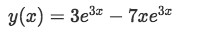
Equation for example 1(e): Particular solution to the differential equation
Example 2:
Compute the particular solution to the given differential equation with initial conditions of y(2)=e3 and y'(2)=(\frac{1}{2})e^{3}
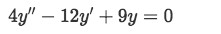
-
Step 1:
Finding the characteristic equation: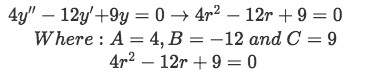
Equation for example 2(a): Characteristic equation -
Step 2:
For the characteristic equation found in this example is more practical to use the quadratic equation in order to find the value of r:
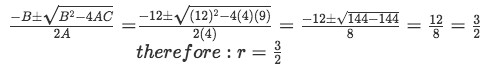
Equation for example 2(b): Finding the repeated root -
Step 3:
Now we plug this value into our equation 10 to obtain the general solution to differential equation for example 2:

Equation for example 2(c): Finding the general solution to the differential equation -
Step 4:
Let us calculate the first derivative of the general solution so we can apply the initial conditions of y(2)=e3 and y'(2)=(\frac{1}{2})e^{3} to both, the general solution and its derivative, to find the values of the two unknown constants on the general solution equation:
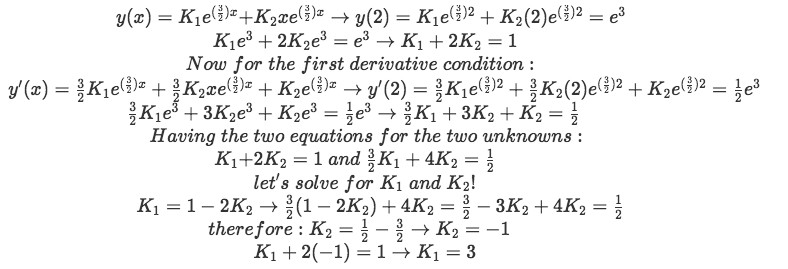
Equation for example 2(d): Finding the values of the unknown constants in the general solution -
Step 5:
And thus, using the found values for the unknown constants we plug them into the general solution to obtain the particular equation solution to the second order constant coefficients linear homogeneous differential equation:
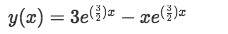
Equation for example 2(e): Particular solution to the differential equation
After working through the examples, you probably noticed what we discussed at the beginning of this lesson: this and the two lessons before are all very similar because they are actually solving the same type of differential equations and looking for the same quadratic form of characteristic equations! Thus, the methodology is very similar, the only differences come from the type of roots one finds on the characteristic equation, and thus is the type of root the one that sets the tone on which method to follow.
In conclusion, when trying to find the solution to a second order constant coefficients linear homogeneous differential equation, the first thing to do is to transcribe it as a characteristic equation, then finding its roots. Depending on which roots you find: real distinct roots, complex roots or repeated roots, you can then decide how to continue and which methodology is the proper one to use in each case.
For more on repeated roots we recommend you to take a look into these notes on differential equations so you can observe a little bit of different methodology and get a different perspective for these problems.
By using the characteristic equation:
Using the quadratic formula:
But what if B2=4AC?
Throughout the videos it will be shown that our solutions are:
y1(x)=e2A−Bx y2(x)=xe2A−Bx
Or in full generality:
Where r1=r2=−2AB
remaining today
remaining today



