Calculating Laplace transforms
What is a Laplace transform?
Reviewing the past lesson, let us talk again briefly about the Laplace transform definition and the Laplace transform properties. We know already that the Laplace transform is a particular integral formula which is useful while solving linear differential equations with certain conditions. We also know that the reason why you will prefer to use the Laplace transformation instead of any other method while solving certain linear differential equations directly, is because this method actually simplifies the process by being algebra-based instead of calculus-based.
In mathematics, we refer as a "transformation" to a method we use to simplify the way we solve a problem, sometimes this means going from the techniques used in a higher level of math to a lower level of the field. In this case, the integral transform which we sometimes might refer as the Laplace integral, is a tool to convert a linear differential equation which is a function of time into an algebraic expression in terms of frequency.
In mathematical notation, the definition of Laplace transform or Laplace integral can be simply put as follows:
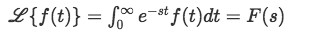
As you may have noted in formula 1, we are dealing with an improper integral in the Laplace transform since the interval of the integration is unbounded. Remember that when one (or both) of the extremes of an integration is infinite we truly do not know the value itself (because is not a real number) and so, we cannot evaluate the integration using the classical Riemann technique.
From our lessons on limits you may remember that you can know the behaviour of a function even though you may not know its value by evaluating its limit as it approaches a particular point. We will use this knowledge when solving improper integrals.
To take the issue of the unbounded interval in the integration out, we take the limit of the integration giving the unbounded side of the integral a constant value, which will approach infinity in the limit operation. In this way, we can easily use regular integration techniques to solve the problem without being worried to evaluate to infinity until we are able to toss away those variables. In simpler words, we want to solve the integration in a way that we get rid of all the t's of the function, so we don't have to worry about evaluating it to infinite, and thus, simplifying the problem by now having the function in other terms.
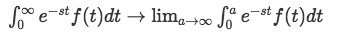
The importance of the Laplace transform will be more obvious to us if we think on the whole process of solving a differential equation with it. A Laplace transform is an operator, this operator will be applied to a differential equation that in principle is difficult to solve for, so the steps go as follows:
First you have a differential equation to which you apply the operator called the Laplace integral (figure 1), this will produce an algebraic expression which is much simpler to solve and obtain a result. After obtaining the information needed from the first equation (say the value of a variable, etc) we can even work backwards to check if our process (and result) is correct, thus giving us a complete cycle of information. For this last step we use the operator called the inverse Laplace transform, and we will dedicate a complete article on it later.
Find the Laplace transform of the following functions:
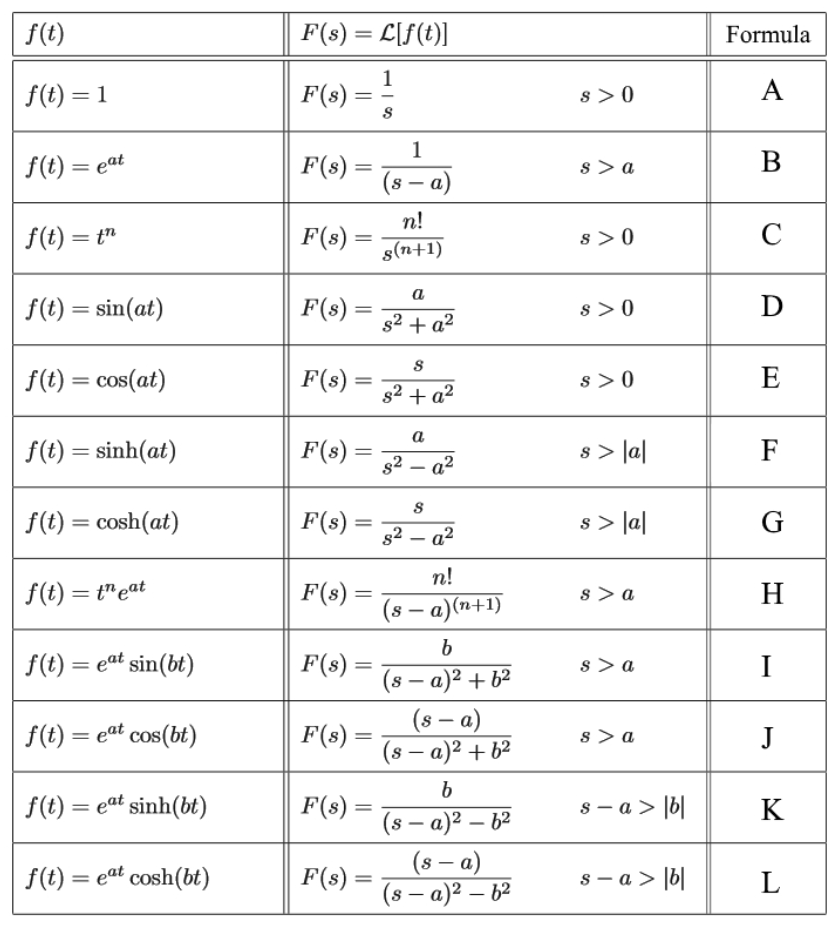
For this lesson we will be using a new methodology to solve Laplace transforms, and that is by comparison with table 1. In the past lesson you learned how to calculate these kind of transformations by working out through the integral operations, but the thing is that these operations can be gathered together in a table where we can come back and check the established result for different types of functions being transformed. This will actually accelerate the way you compute Laplace transformations even more, and with time, you may not even need to go back and look at the table since you may get used to and memorize the results of the Laplace transform of certain functions.
In order to follow the method of comparison with the table, one needs to follow the next steps to solve a Laplace transform:
- Having the Laplace transform to resolve, simplify by linearity if addition or subtraction signs are found inside the function to be transformed.
- Use the Laplace transforms table to solve each of the parts from the separated Laplace function from last step
- Identify the formula from the table which contains the same operation as the one we find in each function to solve
- Once sure of what equation to use from the table, identify element values such as n, a or b (depending on the equation you are using).
- Ordered Item 3
- Transcribe the result, by following the answer on the table, using your values for n, a or b according to the type of function you have.
- After each separated Laplace transform has been solved, put the complete solution to the initial Laplace transform by adding (or subtracting, depending on the signs you had originally) each of the results found per each separated transform.
Next we have a series of Laplace transform problems with answers for you to study, we do recommend that you try to solve them on your own and then come back later to check if your answers are correct.
Laplace transform examples
Now let us work through a few Laplace transform examples using the common Laplace transforms results from our table. As always, we recommend you to try and solve all of the problems on your own first and then come back and check your results.
At this point, we have assumed that you have already studied the lesson on the introduction to the Laplace transform, if you have not done so already, please go back to that section first so you can have a better understanding of the mathematical procedure of calculating the integrals for a Laplace transform. It is important you know that methodology beforehand, although you will be using the comparison method with the table above for the next problems, a deeper understanding will come from having looked at both methods.
Example 1
Calculate the following Laplace transform:
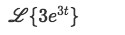
Following the steps listed, notice that in this case there is no need to simplify for linearity, and this we jump right onto step number 2, and so, we identify we need to use formula B form the table of Laplace transforms:
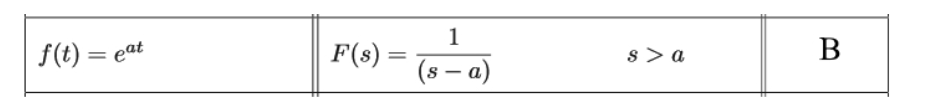
Remember that any constant coefficients can be taken out of the transformation without affecting the result:
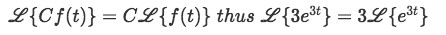
Identifying that for this case a is equal to 3 we work through the solution:
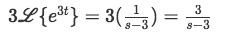
Example 2
Calculate the following Laplace transform:
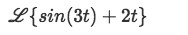
Now that the problem got a little bit lengthier, let us explicitly use the steps listed in the last section to solve the problem:
-
Step 1:
By linearity the Laplace transform can be rewritten as:
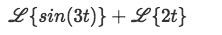
Equation for Example 2(a): Laplace transform separated by linearity -
Step 2:
We use the Laplace transform table to solve each of the resulting transformations separated by linearity through the last step. And so, for the first Laplace transform we select formula D from the table:Where we can easily identify that a=3, and so:
Equation for example 2(b): Identifying the general solution of the Laplace transform from the table For the second Laplace transform of this problem, we can right away notice that we just need to solve for the Laplace transform of t using formula C: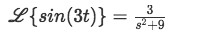
Equation for example 2(c): Solving the first Laplace transform Where n=1, therefore: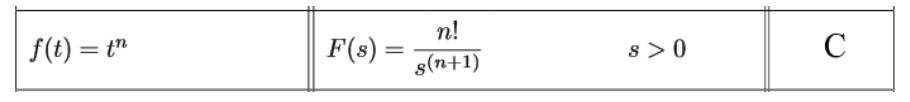
Equation for example 2(d): Identifying the general solution of the Laplace transform from the table 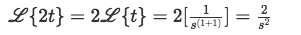
Equation for example 2(e): Solving the second Laplace transform -
Step 3:
We can now form the complete solution to the initial Laplace transform:Although our job is done, we can still play a little bit more with the solution to rearrange it in a way that we have a common denominator for the two expressions, so, this next step is optional, but usually nice to see and sometimes this might be the kind of "elegant" solution you are asked for during a test.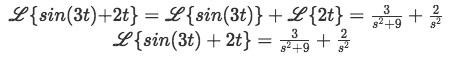
Equation for example 2(f): Complete solution to the Laplace transform 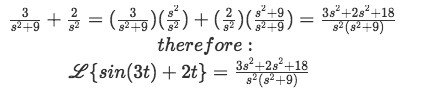
Equation for example 2(g): Final solution for the Laplace transform
Example 3
Calculate the following Laplace transform:
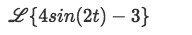
-
Step 1:
By linearity the Laplace transform can be rewritten as:Notice how for the second Laplace transformation is equivalent to taking the transform of 3 times 1, and so, we can take one of the constant factors out to facilitate the operation. Therefore is convenient to take the 3 out because then you are left to solve just for the Laplace transform of 1. This is the same for any other Laplace transform of a constant, you just take the constant out and leave the one inside (which is solvable with formula A from the table).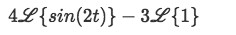
Equation for Example 3(a): Laplace transform separated by linearity -
Step 2:
Again we use our table to solve each of the resulting transformations from the last step. Once more, we use formula D for the first Laplace transform:We identify that a=2, so: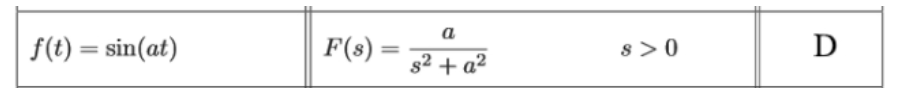
Equation for example 3(b): Identifying the general solution of the Laplace transform from the table For the second Laplace transform we use formula A: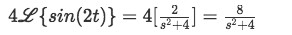
Equation for example 3(c): Solving the first Laplace transform Where you don't need to identify any variable since this is just the Laplace transform of constant 3, so, we just multiply the constant coefficient we took out of the transform in our problem:
Equation for example 3(d): Identifying the general solution of the Laplace transform from the table 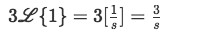
Equation for example 3(e): Solving the second Laplace transform -
Step 3:
We can now form the complete solution to the initial Laplace transform:And once more, we rearrange it in a way that we have a common denominator for the two expressions: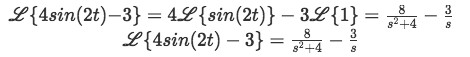
Equation for example 3(f): Complete solution to the Laplace transform 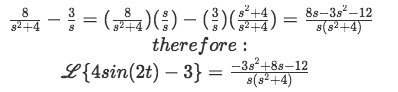
Equation for example 3(g): Final solution for the Laplace transform
Example 4
Calculate the following Laplace transform:
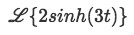
-
In this case, there is no separation we need to do through linearity, so we jump to the second and third steps faster. Using formula F:
We can identify that for this case, a=3, and so we solve the Laplace transform rapidly:

Equation for example 4(a): Identifying the general solution of the Laplace transform from the table 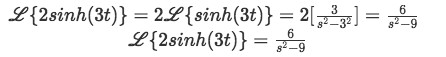
Equation for example 4(b):Final solution for the Laplace transform
Example 5
Calculate the following Laplace transform:
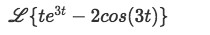
-
Step 1:
By linearity the Laplace transform can be rewritten as: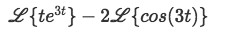
Equation for Example 5(a): Laplace transform separated by linearity -
Step 2:
Using our table to solve each of the resulting transformations, we grab the Laplace transform formula H to solve the first Laplace transform:We identify that n=1 and a=3, so: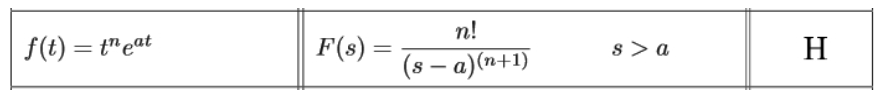
Equation for example 5(b): Identifying the general solution of the Laplace transform from the table For the second Laplace transform we use formula E: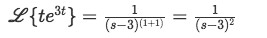
Equation for example 5(c): Solving the first Laplace transform Where a=3, therefore: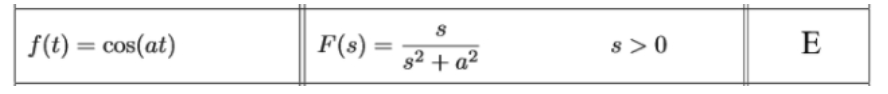
Equation for example 5(d): Identifying the general solution of the Laplace transform from the table 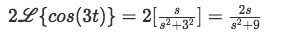
Equation for example 5(e): Solving the second Laplace transform -
Step 3:
The complete solution to the initial Laplace transform is:Using some simple algebra to put the whole expression together with the same denominator: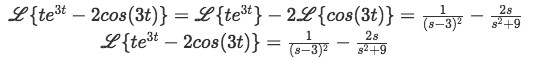
Equation for example 5(f): Complete solution to the Laplace transform 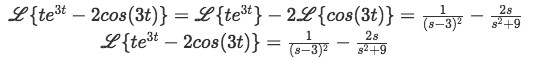
Equation for example 5(g): Final solution for the Laplace transform
Example 6
Calculate the following Laplace transform:
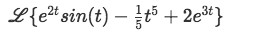
-
Step 1:
Rewriting the Laplace transform due linearity: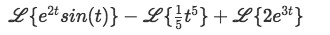
Equation for Example 6(a): Laplace transform separated by linearity -
Step 2:
Using formula I from the table to solve the first of the three Laplace transforms:We obtain that a=2 and b=1, therefore: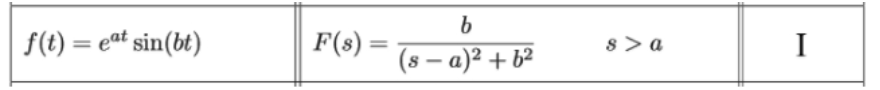
Equation for example 6(b): Identifying the general solution of the Laplace transform from the table For the second Laplace transform we use formula C: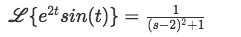
Equation for example 6(c): Solving the first Laplace transform Where n=5, therefore: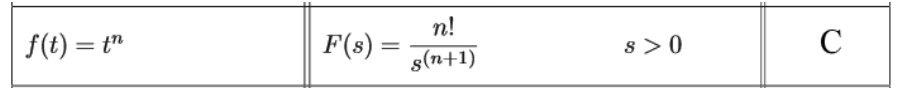
Equation for example 6(d): Identifying the general solution of the Laplace transform from the table And finally for the third Laplace transformation we use formula B: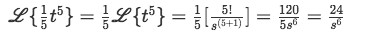
Equation for example 6(e): Solving the second Laplace transform Where a=3, thus: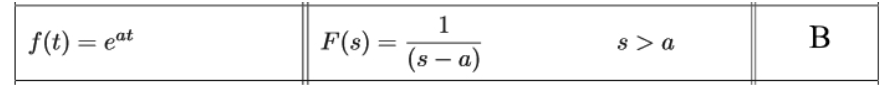
Equation for example 6(f): Identifying the general solution of the Laplace transform from the table 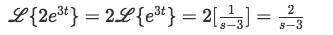
Equation for example 6(g): Solving the second Laplace transform -
Step 3:
Putting the complete solution to the initial Laplace transform together we obtain:Since we are dealing with a lengthy expression of three terms and each with a different denominator, we think is better to just leave it this way in this case, there is just one small simplification we will do and that is in the denominator of the first term in the right hand side: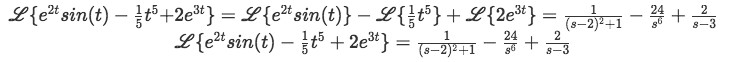
Equation for example 6(h): Complete solution to the Laplace transform 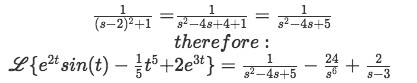
Equation for example 6(i): Final solution for the Laplace transform
After all of this practice you are now ready for our next section where you will be solving differential equations with the Laplace transform.
Before going to the next section, we recommend you to take a look at the flow chart included on this article about the method of solving initial value problems with the Laplace transform. And also, just so you can have an overall view of the topics that we have done recently and the ones that are coming, you can check these Differential equation notes with some perspective on the topic.
Theorem:
If we have the Laplace Transform of two functions:






