Orthogonal sets
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/4
Intros
Lessons
- Orthogonal Sets Overview:
- Orthogonal Sets and Basis
• Each pair of vector is orthogonal
• Linear independent → Form a Basis
• Calculate weights with Formula - Orthonormal Sets and Basis
• Is an orthogonal set
• Each vector is a unit vector
• Linear independent → Form a Basis - Matrix U with Orthonormal columns and Properties
• UTU=I
• 3 Properties of Matrix U - Orthogonal Projection and Component
• Orthogonal Projection of y onto v
• The component of y orthogonal to v
0/5
Examples
Lessons
- Orthogonal Sets and Basis
Is this an orthogonal set?
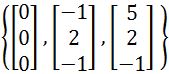
- Verify that
 is an orthogonal basis for R2, and then express
is an orthogonal basis for R2, and then express 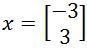 as a linear combination of the set of vectors in B.
as a linear combination of the set of vectors in B. - Orthonormal Sets/Basis
Is set B is an orthonormal basis for R3?
- Let
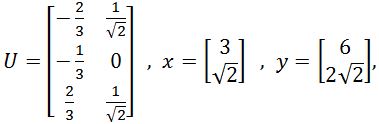 where U has orthonormal columns and UTU=I. Verify that
where U has orthonormal columns and UTU=I. Verify that
(Ux)⋅(Uy)=x⋅y - Orthogonal Projection
Let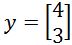 and
and 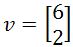 . Write y as the sum of two orthogonal vectors, one in Span{v} and one orthogonal to v.
. Write y as the sum of two orthogonal vectors, one in Span{v} and one orthogonal to v.
Free to Join!
StudyPug is a learning help platform covering math and science from grade 4 all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Orthogonal sets
What does orthogonal mean?
Remember from our past lesson on the inner product, length and orthogonality that we defined two vectors as orthogonal if they were perpendicular to each other (in general, any orthogonal lines happen to be lines which are perpendicular, and so, orthogonal vs perpendicular is just the same). For linear algebra we focus on the concept in the sense that we are now not only thinking in two dimensions (thus orthogonal lines) but we want to expand our view into three dimensions (due to the scenarios which can be encountered in our world given that we live in a tridimensional space), and so we start using the word orthogonal meaning the perpendicularity of not only lines but planes and spaces, opening the field for the mathematical calculations we can compute and the cases that can be studied.
In the next diagram, you can see an example of orthogonal vectors:
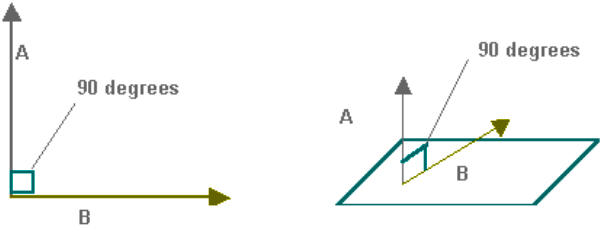
Mathematically speaking, orthogonal means that when you compute the inner product of two vectors, the result must be zero for the vectors to be orthogonal. For example, if any set of two vectors each lying in a different plane (without being an axis for the panes) of the orthogonal planes shown below, will be automatically orthogonal since their components can be observed to be orthogonal.
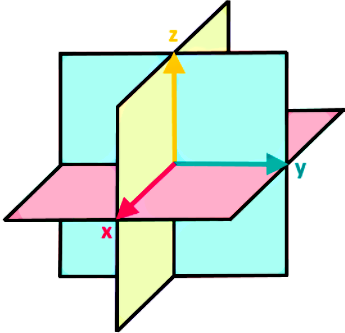
Before we continue, let us remind you that the inner product of two vectors is the same as the dot product, or scalar product between two vectors, and thus, we will be using these terms interchangeably during the lesson.
How to find orthogonal vector set
So, answer quickly: how to tell if two vectors are orthogonal to each other? The dot product! Keep this fresh in your head!
To formally define orthogonal sets with this in mind: A set of vectors {v1,v2,...,vn} in Rn are orthogonal sets if each pair of vectors from the set are orthogonal to each other. And this means that the inner product (dot product) of the vectors within the set is equal to zero as:
Note that for equation 1, the subindexes i and j cannot be equal, so this equation works when i ≠ j since them being equal would mean that we are multiplying the vector with itself and would result in the magnitude of the vector squared.
With this in mind, if the set of vectors {v1,v2,...,vn} in Rn is an orthogonal set, then this is enough to prove linear independence for these vectors. Thus, the vectors form a basis for a subspace S, and this basis is what we call the orthogonal basis.
To check if a set is an orthogonal basis in Rn, we can simply verify if this is an orthogonal set.
Remember from our lesson about the linear combination and vector equations Rn that a linear combination of vectors v1,v2,...,vp is defined as:
Where i=1,2,...,p and the constants c1,c2,...,cp can be calculated using the formula:
Since it is said that an orthogonal set of vectors is a set where all the vectors are linearly independent, we can use this formula for a linear combination to solve for the vector x defined in equation 2. Therefore, for finding orthogonal vectors within a set, being able to define a set as orthogonal and find the orthogonal basis, we need to follow the next steps:
- Determine if the vectors given in the set are orthogonal by computing the dot products of them by pairs.
- If the result of each pair of vectors dot product was zero, then the vector set is an orthogonal set.
- If the set is orthogonal, then is forms and orthogonal basis.
- We can prove this by writing the vector of the linear combination containing the vectors from the set.
We will take a look at a few examples of such operations in our next section. For exercise example 1 we will need to follow only steps 1 and 2; while for exercise example 2 we will need to follow all three steps, it just depends on whatever you are asked but the process itself is pretty straightforward.
Now, what happens if you are asked for an orthonormal basis? Notice: NOT orthogonal.
Well, a set of vectors {v1,v2,...,vn} is an orthonormal set if is an orthogonal set of unit vectors, in other words, all of the vectors within the set must be orthogonal to each other, plus, they must all have a magnitude (length) of one. Having a subspace S spanned by such orthonormal set we say that the vectors inside of it form an orthonormal basis, and this is easily understood because we already know that all of the vectors inside the set are linearly independent of each other since this is a condition for an orthogonal set.
Following with the definition of orthonormal, we can check if the column vectors belonging to the columns of a matrix are orthonormal by performing the next matrix multiplication:
Where U is a m×n matrix with columns that are orthonormal vectors. And I is the identity matrix.
With equation 4 in mind, if we have this m×n matrix U containing orthonormal columns and a pair of vectors x and y in Rn, then we have the following three equation identities to be true:
Now that you know what is orthogonal (and non orthogonal for that matter), how to tell if two vectors are orthogonal and even know how to find orthogonal vectors and sets of them, it is time we work through a few examples.
Finding orthogonal vectors
During the next four problems we will use our knowledge on the orthogonal definition applied to vectors, sets, basis and then how it develops into orthonormality. So have fun solving the exercises!
Example 1
Having a set of three vectors as shown below: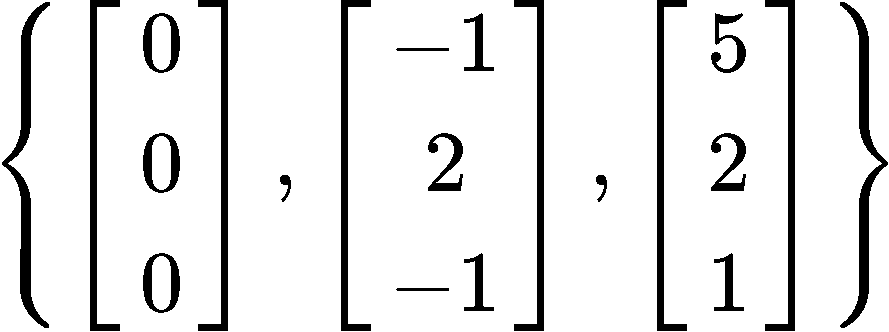
Is this an orthogonal set?
In order for us to prove if the set is orthogonal, we have to determine whether the given vectors are orthogonal, parallel, or neither. And how do we do that? With the dot product! Remember that the dot product of orthogonal vectors is equal to zero, therefore, we just have to obtain the dot product of all of these vectors with each other and see the results.
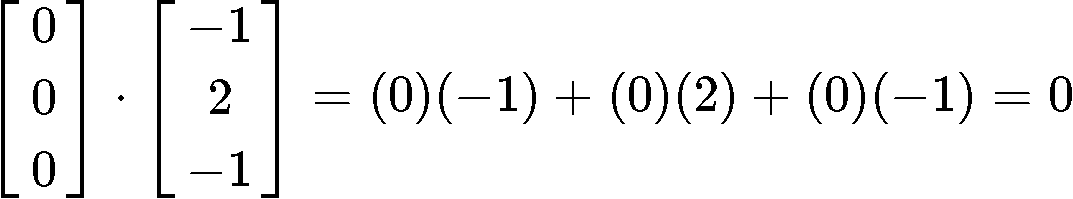
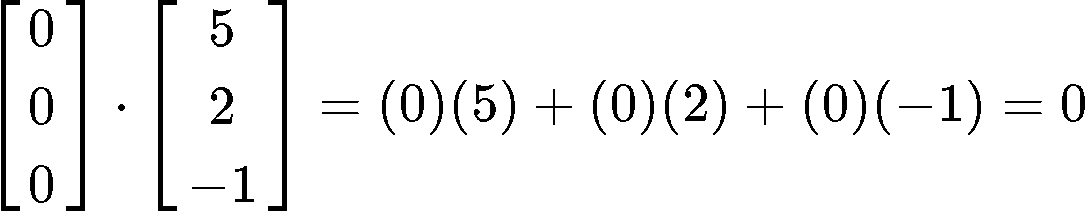
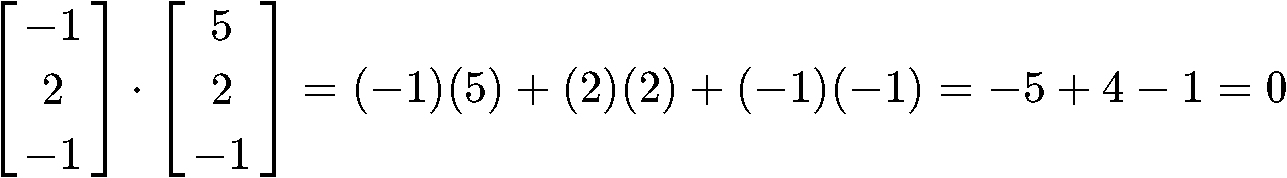
Since all of the dot product operations resulted in zeros, then it means that the three vectors in the set are all orthogonal to each other, and therefore, this is an orthogonal set of vectors.
Example 2
Given the set B and the column vector x as defined below:
Verify that B is an orthogonal basis for R2, and then express x as a linear combination of the set of vectors in B.
So we start by verifying the orthogonality of v1 and v2, the two vectors in the set called B; for that, we get the dot product v1⋅v2:
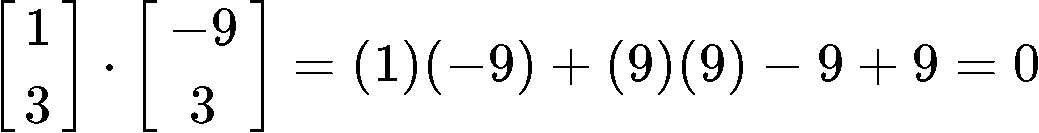
A result of zero for the dot product tells us that the set B is a set of orthogonal vectors.
Then, our next step is to express x as a linear combination of the set of vectors in B. Using equation 2 we write the linear combination of the vectors from set B and express it as vector x:
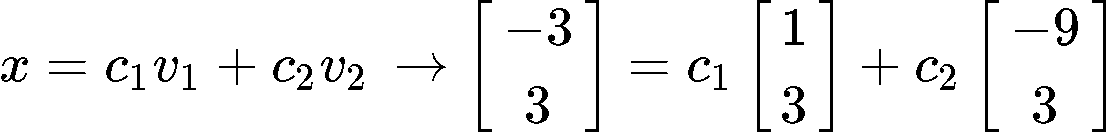
All that is left to complete this expression is to find the values of the constants c1,c2. Using equation 3 we have that:
And so, we rewrite the linear combination including the found values of c1 and c2:
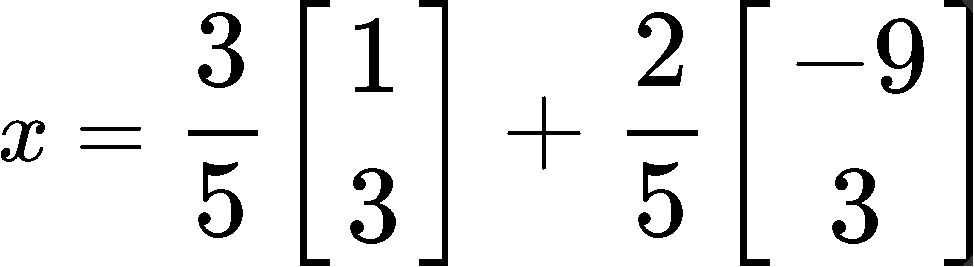
Example 3
Having set B of vectors (as defined below), is set B an orthonormal basis for R3?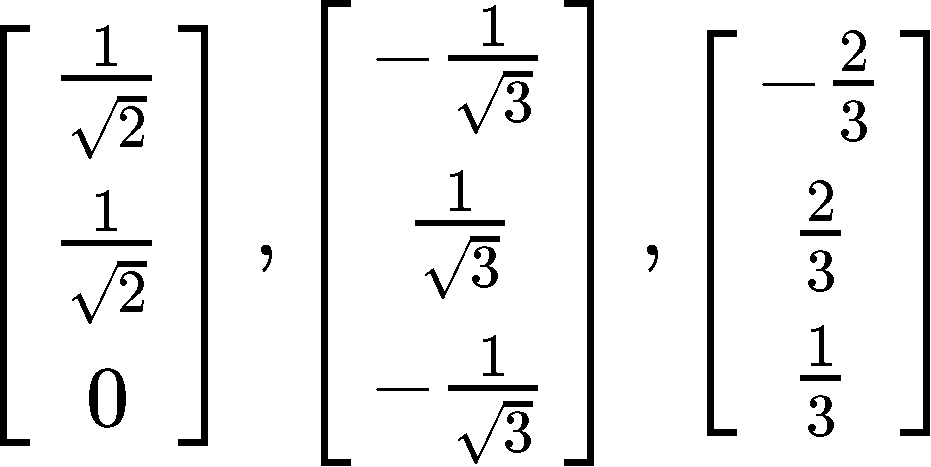
In order to prove that this is an orthonormal basis for R3, we need to prove this is an orthonormal set. Remember that a set of orthonormal vectors is that which is composed of vectors which are orthogonal to each other and at the same time, they are all unit vectors. So, let us prove the orthogonality of the vectors in the set first:

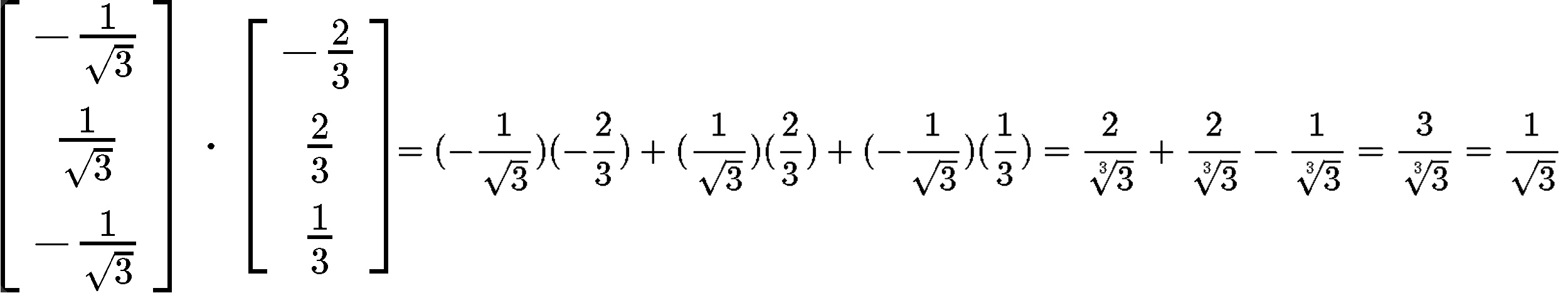

Example 4
Let U, x and y be as defined below, where U has orthonormal columns and UTU=I.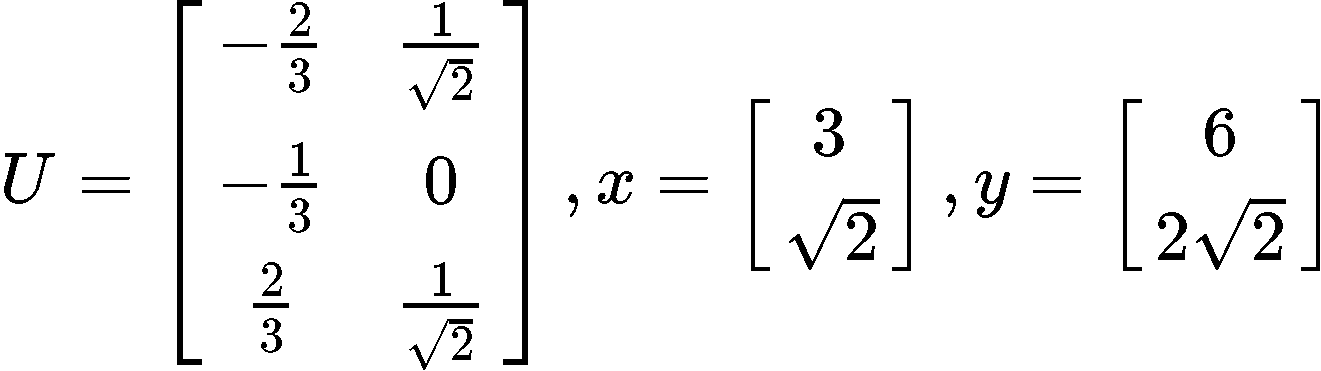
Now, verify that:
We will solve this problem by parts, the left hand side and the right hand side. Since the right hand side will be shorter to solve, lets start by doing that dot product first:
Now working through the right hand side of the equation to verify:
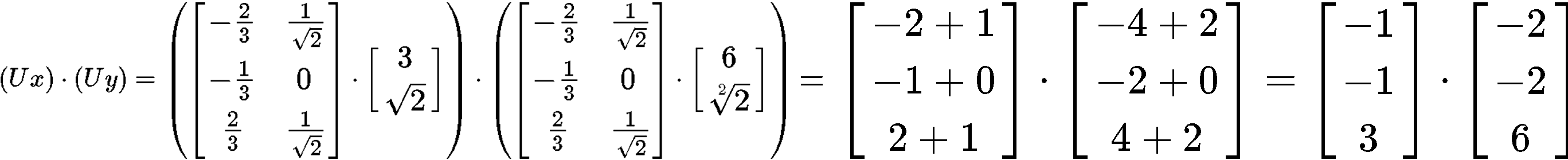
Notice the results from both sides of equation 15 yield the value of 22, and therefore, the expression is proved correct.
Now that you have learnt about orthogonality and vector sets with this characteristic, we recommend you to visit this lesson on orthogonal sets which includes a variety or detailed problems that can supplement your studies.
In our next lesson we will introduce the concept of orthogonal projection, which of course is closely tied to the definitions we saw during this lesson. So we hope that you have enjoyed our lesson of today, and this is it, see you in the next one!
A set of vectors {v1,⋯,vn} in Rn are orthogonal sets if each pair of vectors from the set are orthogonal. In other words,
vi⋅vj=0
Where i=j.
If the set of vectors {v1,⋯,vn} in Rn is an orthogonal set, then the vectors are linearly independent. Thus, the vectors form a basis for a subspace S. We call this the orthogonal basis.
To check if a set is an orthogonal basis in Rn, simply verify if it is an orthogonal set.
y=c1v1+c2v2+⋯+cpvp
Are calculated by using the formula:
ci=vi⋅viy⋅vi
where i=1,⋯,p.
A set {v1,⋯,vp}is an orthonormal set if it's an orthogonal set of unit vectors.
If S is a subspace spanned by this set, then we say that {v1,⋯,vp} is an orthonormal basis. This is because each of the vectors are already linear independent.
A m×n matrix U has orthonormal columns if and only if UTU=I.
Let U be an m×n matrix with orthonormal columns, and let x and y be in Rn. Then the 3 following things are true:
1) ∥Ux∥=∥x∥
2) (Ux)⋅(Uy)=x⋅y
3) (Ux)⋅(Uy)=0 if and only if x⋅y=0
Consider L to be the subspace spanned by the vector v . Then the orthogonal projection of y onto v is calculated to be:
y^=projLy=v⋅vy⋅vv
The component of y orthogonal to v (denoted as z) would be:
z=y−y^
If the set of vectors {v1,⋯,vn} in Rn is an orthogonal set, then the vectors are linearly independent. Thus, the vectors form a basis for a subspace S. We call this the orthogonal basis.
To check if a set is an orthogonal basis in Rn, simply verify if it is an orthogonal set.
Are calculated by using the formula:
A set {v1,⋯,vp}is an orthonormal set if it's an orthogonal set of unit vectors.
If S is a subspace spanned by this set, then we say that {v1,⋯,vp} is an orthonormal basis. This is because each of the vectors are already linear independent.
A m×n matrix U has orthonormal columns if and only if UTU=I.
Let U be an m×n matrix with orthonormal columns, and let x and y be in Rn. Then the 3 following things are true:
1) ∥Ux∥=∥x∥
2) (Ux)⋅(Uy)=x⋅y
3) (Ux)⋅(Uy)=0 if and only if x⋅y=0
Consider L to be the subspace spanned by the vector v . Then the orthogonal projection of y onto v is calculated to be:
The component of y orthogonal to v (denoted as z) would be:
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



