Sign In
Sign Up
flag-us

Subtracting decimals

Topic Notes

In this lesson, we will learn:

  • How to subtract decimal numbers using base ten (block) models
  • That subtracting decimal numbers is the same as subtracting whole numbers, which involves lining up the right place values and exchanging

Notes:

  • To subtract decimals with base ten (block) models:
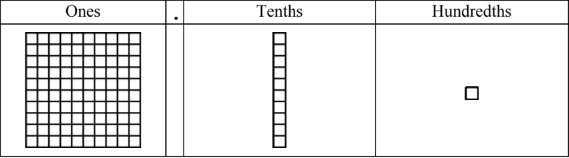
    • Remember the three types of blocks used to represent the ones, tenths, and hundredths place values
      • "One whole" or hundred block = ones place value
      • Column (stick or rod) = tenths place value
      • Single square = hundredths place value
Adding Decimals
    • A subtraction statement is made of: minuend - subtrahend = difference
    • Cross out the blocks that you are subtracting (subtrahend from the minuend), until you've crossed out all matching pairs (subtrahend all crossed out).
    • Exchange (or "borrow") from a bigger block if you don't have enough blocks to cross out. One big block can be split into 10 of the next smaller type of block (next place value).

Adding Decimals

  • To subtract decimals, line up the decimal point to make sure you are adding the right place values in the same columns. Exchange (borrow) whenever necessary.
    • Sometimes, you will have to write one or more extra zeroes to a number after the decimal point (trailing zeroes) when the minuend/subtrahend don't have the same number of place values.